Шагающие роботы

Устойчивость

Для того чтобы какое-либо тело при движении находилось в устойчивом положении, в общем случае необходимо, чтобы оно имело опору по крайней мере в трех точках. Следовательно, чтобы шагающий аппарат был устойчивым, ему необходимы по крайней мере три ноги. Вместе с тем человек пользуется при ходьбе двумя ногами и обладает достаточно большой устойчивостью. Более того, при необходимости он способен перемещаться даже на одной ноге - прыжками. Можно привести множество примеров двуногой ходьбы, которыми так щедро представлено царство фауны. Однако создание мобильных роботов, способных передвигаться на двух ногах так же устойчиво, как и человек, сопряжено с огромными трудностями, и основная из них заключается как раз в разработке методов, обеспечивающих динамическую устойчивость двуногого шагающего аппарата. В этой связи интересно понаблюдать за движением двуногой игрушки. Обычно эти игрушки конструируются таким образом, что движение одной ноги совершенно не влияет на состояние другой, а проекция центра тяжести игрушки всегда приходится на площадь, занимаемую стопой одной из ног (рис. 4.22). Естественно, что такая конструкция обладает достаточно большой устойчивостью, и игрушка практически не падает. Однако подобный способ передвижения вряд ли можно назвать динамической двуногой ходьбой. Скорее всего, он сродни ходьбе приставными шагами. Ходьбой в полном смысле этого слова можно назвать способ перемещения шестиногого шагающего аппарата. В этом случае на каждом шаге корпус аппарата поочередно опирается на три конечности - две с одной стороны и одну с другой; на следующем шаге - наоборот Таким образом, шестиногий аппарат обладает как статической, так и динамической устойчивостью. Обсудим подробнее проблемы обеспечения статической устойчивости шагающих аппаратов.

Рис 4.22. Когда игрушка стоит на левой ноге, проекция ее центра тяжести находится в затушеванной зоне. При смене ног проекция центра тяжести по-прежнему остается в этой зоне. Вот почему игрушка не падает

Прежде всего уточним, какое все-таки минимальное количество ног необходимо для того, чтобы придать устойчивость аппарату. Как уже отмечалось, любой трехногий робот можно сделать устойчивым, но при условии, что он будет находиться в неподвижном состоянии. Совершенно очевидно, что никакими силами не удастся обеспечить статическую устойчивость этого робота в процессе ходьбы. Относительно легко сделать устойчивым как в неподвижном состоянии, так и в процессе движения робот с четырьмя ногами. Тем не менее даже в этом случае для обеспечения статической устойчивости движущегося робота в процессе управления требуется решать два не совсем простых вопроса: в какую сторону должен перемещаться центр тяжести шагающего аппарата в данный момент времени и по какому закону должно происходить изменение скоростей свободных ног и опорных конечностей педипулятора? Явное управление изменением направления перемещения центра тяжести после каждого шага робота приводит к тому, что на малых скоростях четвероногий робот в отличие от животных передвигается неестественной рыскающей из стороны в сторону походкой. В этом заключается один из недостатков конструкции мобильных роботов с четырьмя ногами.

Характерные особенности движения четырехногого механизма иллюстрируется на рис. 4.23. Как следует из рассмотрения диаграммы 1 (рис. 4.23), когда робот находится в покое, стоя на четырех ногах, его центр тяжести G, как правило, совпадает с геометрическим центром четырехугольника, вершинами которого являются точки опоры ног. Если одна из ног чуть-чуть приподнимается над опорной поверхностью и вытягивается в направлении Движения робота, устойчивость корпуса должна обеспечиться за счет остальных трех ног. Поскольку при перемещении приподнятой ноги в точку А центр тяжести всей системы также смещается из исходного положения G в направлении перемещения на соответствующую величину, робот потеряет равновесие и неизбежно упадет, если не будут приняты какие-либо меры по обеспечению его устойчивости. Для восстановления устойчивости, очевидно, необходимо, чтобы центр тяжести робота с одной приподнятой ногой из точки G переместился в точку G₁₁, находящуюся внутри треугольника BCD (диаграмма 2). Аналогичная ситуация возникает, когда приподнимается и переносится вперед нога D. В этом случае корпус сохраняет равновесие, опираясь на три ноги, которые касаются опорной поверхности в точках А₁, В и С, при этом центр тяжести робота перемещается из точки G₁₁ в точку G₁₂ (диаграмма 3). То же самое происходит при выполнении шага ногой В (диаграмма 4). На этот раз для сохранения устойчивости после завершения шага центр тяжести робота должен находиться внутри треугольника A₁CD₁. Наконец, если в движение приходит нога G, то центр тяжести окажется внутри треугольника A₁B₁D₁ (диаграмма 5). Следовательно, при движении четырехногого шагающего аппарата его центр тяжести должен менять свое положение после каждого шага, выполняемого любой из ног. Таким образом, обеспечение высокой скорости и плавности движения для данной конструкции шагающего аппарата оказывается довольно сложной задачей. Но тогда возникает вопрос; каким же образом четвероногие животные, в частности лошадь и собака, умудряются двигаться не только быстро, но и плавно? Чтобы ответить на этот вопрос, Мейбридж занялся изучением походки этих животных. Он заснял бег лошади на кинопленку и, внимательно проанализировав работу конечностей животного, пришел к выводу, что в процессе движения кончик каждой ноги перемещается по некоторой криволинейной траектории - циклоиде. Результаты исследования работы ног лошади при перемещении обычным прогулочным шагом представлены на рис. 4.24. Как следует из рисунка, при таком способе передвижения в каждый момент времени земли касается не менее двух копыт. Приглядевшись, можно заметить, что в очень короткие промежутки времени земли касаются сразу три копыта. Обычной считается ситуация, при которой две передние (или задние) либо две правые (или две левые) ноги лошади находятся на земле, в то время как две остальные - в воздухе. В процессе движения указанные пары ног периодически меняются ролями. Таким образом, не обладая в каждый момент бега статическим равновесием, лошадь сохраняет устойчивость за счет динамической балансировки.

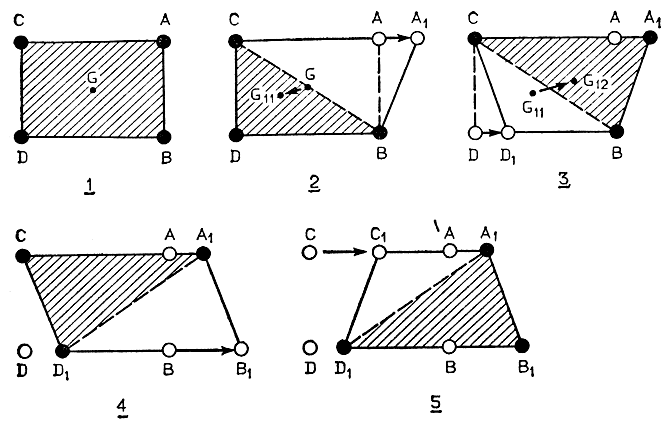
Рис. 4.23. Принудительное смещение центра тяжести для обеспечения статической устойчивости при ходьбе шагающего аппарата с четырьмя конечностями

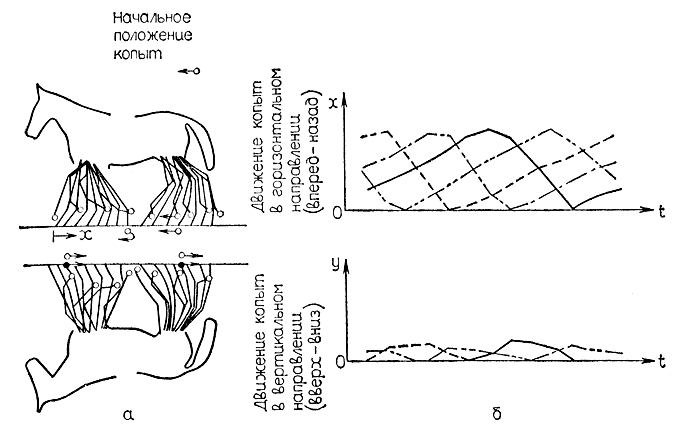
Рис. 4.24. Диаграммы перемещения копыт лошади при ходьбе прогулочным шагом. (Диаграммы получены при помощи съемочного устройства, разработанного Майбриджем.) а - кинограммы движения копыт, полученные совмещением кадров во времени: вверху - правая передняя и задняя ноги; внизу - левая передняя и задняя ноги; б - диаграмма колебания копыт в вертикальном и горизонтальном направлениях в течение одного цикла ходьбы. ^____ правая передняя нога; -··- правая задняя нога; ---- левая передняя нога; -·-·- левая задняя нога

На рис. 4.25 и 4.26 приводятся результаты исследований работы ног лошади в процессе галопа и рыси. Нетрудно заметить, что при переходе с обычного прогулочного шага на галоп или рысь время, в течение которого земли касаются только две ноги, увеличивается.

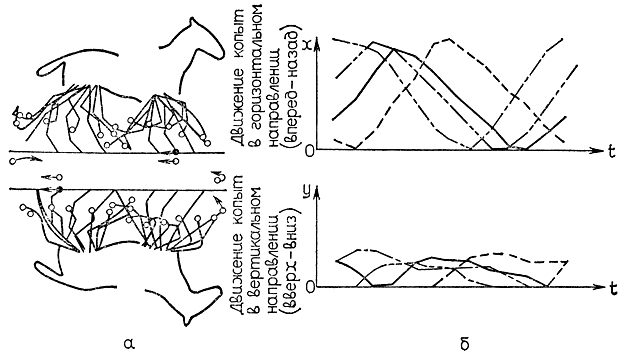
Рис. 4.25. Диаграммы перемещения копыт лошади при движении галопом. a - кинограммы движения копыт, полученные совмещением кадров во времени; б - диаграммы колебания копыт в вертикальном и горизонтальном направлениях в течение одного цикла галопа

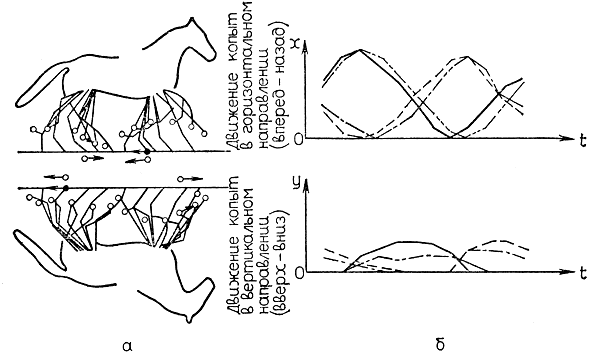
Рис. 4.26. Диаграммы перемещения копыт лошади при движении рысью. a - кинограммы движения копыт, полученные совмещением кадров во времени; б - диаграммы колебания копыт в вертикальном и горизонтальном направлениях в течение одного цикла ходьбы

Анализ кинограмм бега лошади и других животных позволяет сделать общее заключение, что при ходьбе все высшие млекопитающие поддерживают равновесие главным образом за счет динамической, а не статической балансировки. Именно высокая динамическая устойчивость позволяет им перемещаться с любой скоростью, сохраняя при этом плавность движений. Из этого правила есть, конечно, и исключения. Например, ленивец, который также относится к высшим млекопитающим, обычно передвигается по деревьям приставными шагами, поочередно хватаясь передними и задними лапами за ветви. Очевидно, на каждом шаге он сохраняет статическую устойчивость: можно часто наблюдать, как, перебираясь по веткам, он неожиданно замирает и висит неподвижно на одной лапе.

Взаимодействие ног в процессе ходьбы

Работу ног при движении шагающего аппарата будем называть процессом ходьбы. В процессе ходьбы каждая нога может находиться в одном из двух принципиально различных состояний:

● опорное положение - в это время нога касается поверхности и служит опорной для корпуса аппарата;

● свободное положение - в это время нога находится над поверхностью и "готовится" к выполнению опорных функций на следующем шаге.

В процессе ходьбы ноги шагающего аппарата попеременно занимают то опорное, то свободное положения, причем в течение одного цикла каждая нога занимает то и другое положение один раз. Последовательность, в которой при ходьбе происходит чередование опорного и свободного положений всех ног аппарата, определяет конкретный способ его передвижения или его походку. Как уже отмечалось, чередование положений ног при любой походке происходит периодически. Последовательность чередований ног за один период называется циклом ходьбы, а расстояние, которое проходит аппарат за один цикл, - шагом.

Для сохранения шагающим аппаратом статической устойчивости при движении необходимо, чтобы в каждый момент времени в одном положении находилось не менее трех ног. Поэтому число шесть является минимальным количеством ног, с помощью которых шагающий аппарат может поддерживать статическую устойчивость без принудительного смещения положения центра тяжести после поднятия или опускания любой ноги. Справедливость подобного утверждения демонстрируется с помощью диаграмм ходьбы шестиногого аппарата, приведенных на рис. 4.27.

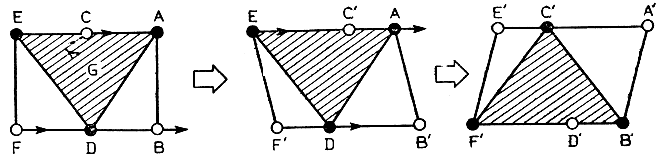
Рис. 4.27. Движение шагающего аппарата с шестью конечностями с сохранением статической устойчивости

Предположим, что в начальном состоянии аппарат опирается на три ноги A, D и Е (центр тяжести G - внутри треугольника ADE), а три другие ноги В, С и F из свободного состояния перемещаются в новое опорное положение - точки В', С' и F' соответственно. Тогда по окончании движения ног В, С и F центр тяжести окажется внутри треугольника B'C'F', а ноги А, D и Е перейдут в свободное положение и начнут перемещаться в точки A', D' и Е'. В процессе ходьбы два описанных состояния будут чередоваться, однако в любом случае центр тяжести останется внутри заштрихованной области, в результате чего сохраняется статическая устойчивость.

Если механизм крепления ног к корпусу допускает движения не только прямо вперед (или прямо назад), то шестиногий робот сможет перемещаться в любую сторону. Поскольку работа ног при этом будет осуществляться в той же последовательности, что и при ходьбе только прямо вперед, статическая устойчивость сохранится. Более того, если имеется возможность изменять скорость движения каждой из ног, то законы изменения этих скоростей можно подобрать таким образом, чтобы статическая устойчивость обеспечивалась даже при движении четвероногого шагающего аппарата.

Движения, совершаемые любой из ног при чередовании опорного и свободного положений в процессе ходьбы, можно упрощенно разделить на фазу поступательного перемещения и фазу восстановления. В простейшем случае переход от первой фазы ко второй может осуществляться за счет движений ноги вверх-вниз строго по вертикали (рис. 4.28). Однако энергия шагающего аппарата будет расходоваться более эффективно, если в течение фазы восстановления нога будет перемещаться по некоторой кривой. Одна из возможных форм криволинейной траектории восстановления показана на рис. 4.29.

Рис. 4.28. Идеализированный цикл перемещения стопы конечности при движении шагающего аппарата

Рис. 4.29. Идеализированный цикл работы конечности шагающего аппарата

По какой бы траектории ни двигалась нога в фазе восстановления для выполнения шага она должна обладать по крайней мере двумя степенями подвижности: подниматься вверх-вниз по вертикали и покачиваться вперед-назад по горизонтали. Правда, в исключительных случаях удается обойтись механизмами с одной степенью подвижности. Например, было разработано несколько конструкций, в которых имитирующее шаг движение осуществляется путем простого поворота

Среди механических ног с двумя степенями подвижности наиболее широкое распространение получили конструкции следующих двух типов:

● нога состоит из двух звеньев, и каждое из них имеет одну вращательную степень подвижности;

● нога образована одной телескопической парой, которая помимо удлинения-сокращения имеет еще одну степень подвижности - вращение в точке подвеса.

Помимо таких конструкций было предложено несколько кинематических механизмов, в которых шаговое движение выполнялось путем прямолинейных перемещений.

♦♦♦ Заметим, что при некоторых способах ходьбы двух степеней подвижности может оказаться недостаточно, например в случае, когда на каждом шаге требуется проводить принудительное перемещение центра тяжести аппарата (рис. 4.23).

Оригинальный метод управления нижними конечностями робота при чередовании опорных и свободных положений предложил Макги (рис. 4.30)^*. Этот метод ориентирован на двухзвенные механизмы конечностей с двумя вращательными степенями подвижности (рис. 4.31). Д-ром Икэда и д-ром Носаки из Научно-исследовательского центра проблем механики был разработан шагающий аппарат с четырьмя конечностями, каждая из которых реализована с помощью пантографического механизма (рис. 4.32). Д-р Икэда построил робот с шестью конечностями, используя в качестве ног кинематические механизмы с одной вращательной и одной поступательной (удлинение-сокращение) степенями подвижности. Еще один шагающий аппарат с оригинальной конструкцией конечностей был создан под руководством д-ра Хиросэ из Токийского технологического института. Каждая из четырех конечностей робота выполнена в виде объемного пантографического механизма. На основе таких же объемных пантографических механизмов Хиросэ удалось построить и манипулятор робота. Для этого потребовалось лишь установить датчики для измерения углов, образуемых звеньями пантографических механизмов в пространстве^**.

^* (Государственный университет шт. Огайо, США.)

^** (Считают, что применение объемных пантографических механизмов в промышленной робототехнике окажется весьма эффективным.)

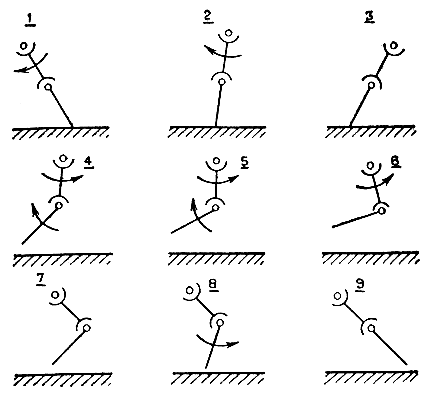
Рис. 4.30. Цикл управления работой конечности шагающего аппарата. 1 - начало рабочей фазы; 2 - продолжение рабочей фазы; 3 - окончание рабочей фазы; 4 - начало фазы восстановления; 5 - продолжение фазы восстановления; 6 - максимальный сгиб конечности в коленном шарнире; 7 - максимальное подтягивание обоих звеньев конечности (достижение максимальных углов поворота в шарнирах); 8 - промежуточная величина сгиба конечности в коленном шарнире; 9 - конец фазы восстановления

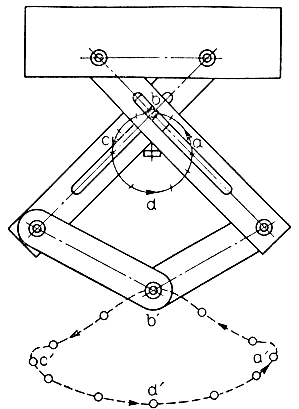
Рис. 4.31. Пантографический механизм в устройстве конечности четырехногого шагающего аппарата

При рассуждении о том, каким минимальным числом степеней подвижности должна обладать каждая нога шагающего аппарата, неявно предполагалось, что корпус робота перемещается строго прямолинейно. Как оказалось, справедливо и обратное утверждение, т. е. если каждая нога робота располагает только двумя степенями подвижности, а его корпус не имеет специального механизма для изменения ориентации в пространстве, то такой робот может двигаться только в прямолинейном направлении. Для изменения направления движения робота только за счет работы ног необходимо, чтобы каждая его нога обладала по крайней мере тремя степенями подвижности. Одна из самых простых конструкций механической ноги с тремя степенями подвижности показана на рис. 4.32.

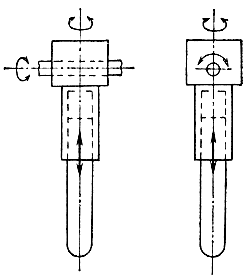
Рис. 4.32. Устройство механической ноги с тремя степенями подвижности

Анализ шагающих механизмов

Возможные способы перемещения механических устройств можно разделить на два больших класса - перемещение на колесах (колесные транспортные средства) и перемещение с помощью ног (шагающие аппараты). Обладая целым рядом преимуществ по сравнению с колесными средствами, шагающие аппараты уступают им по некоторым важным показателям. Принципиальное различие двух способов перемещения состоит в характере движения центра тяжести аппарата относительно корпуса. При движении колесных средств центр тяжести не изменяет своих координат в системе, связанной с корпусом. При перемещении аппарата с шестью и большим числом конечностей центр тяжести также может оставаться неподвижным, однако у большинства шагающих аппаратов при ходьбе центр тяжести смещается по вертикали.

♦♦♦ Интересно отметить, что животные, если только они не умеют плавать или летать, перемещаются почти исключительно с помощью ног. Существуют, правда, и другие способы перемещения по земле (природа создала немало ползающих или извивающихся при движении существ), тем не менее в животном мире самым распространенным способом перемещения является ходьба.

Рассмотрим метод управления искусственными шагающими аппаратами на примерах конкретных устройств. Весьма показательным в этом отношении является "Кибернетический автомат" Томовича, способный автономно перемещаться в произвольном направлении без помощи колес. Как следует из рис. 4.33, перемещаясь за один шаг из точки 0 в точку 0', "Кибернетический автомат" движется по выпуклой относительно опорной поверхности кривой, сначала поднимаясь на некоторую высоту, а затем опускаясь до исходного уровня. При этом центр тяжести "Кибернетического автомата" совершает колебательные движения в вертикальной плоскости. Вместе с тем, если бы корпус автомата был установлен на колесах, то в процессе его движения центр тяжести описывал бы прямолинейную траекторию с началом в точке 0 и концом в точке 0'.

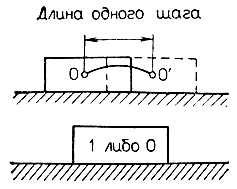
Рис. 4.33. Траектория движения стопы конечности шагающего аппарата 'Кибернетический автомат'. Рис. 4.34. Представление цикла работы конечности шагающего аппарата "Кибернетический автомат" в виде бинарной модели предельных состояний

"Кибернетический автомат", подобно любым другим педипуляторам, перемещается за счет непрерывного чередования опорного и свободного положений каждой из ног в определенной последовательности. Диаграмма, приведенная на рис. 4.34, иллюстрирует такую смену положений для какой-либо одной из ног. Данная диаграмма отражает только сам факт касания опорной поверхности ноги, но не учитывает характера движения ноги в воздухе между двумя последовательными касаниями. Другими словами, она является очень упрощенной абстрактной моделью. Тем не менее такая модель позволяет достаточно точно описывать процесс ходьбы любого шагающего аппарата. В дальнейшем подобные диаграммы будем называть моделями предельных состояний.

В самом деле, чтобы иметь возможность в каждый момент времени отображать состояние шагающего аппарата с n конечностями, достаточно располагать набором из n пар цифр - нулей и единиц. Говоря более строго, текущее состояние n-го педипулятора может быть описано n-мерным вектором, каждая компонента которого является либо нулем, либо единицей.

Томович и Макги применили модели предельных состояний при разработке теоретических основ построения шагающего робота "Кибернетический автомат". Эти модели оказались особенно полезными в процессе проектирования управляющих алгоритмов и соответствующего устройства управления ходьбой данного шагающего аппарата, которое получило название "Кибернетический привод". Обсудим основные особенности привода.

Нога любого животного обычно состоит из нескольких костей (звеньев), которые последовательно соединяются между собой в суставах (шарнирах). Каждая кость прикрепляется к суставу с помощью двух групп мышц, которые находятся в непрерывном противодействии друг с другом. Когда одна группа мышц сокращается, другая расслабляется, и наоборот. При сокращении одной группы мышц соответствующая кость в суставе вращается в одну сторону, а при сокращении другой группы мышц вращение происходит в противоположном направлении. В свободном состоянии, когда мышцы и той и другой группы почти не напрягаются, звенья конечности просто слегка покачиваются в суставах, а когда все мышцы напряжены, конечность жестко фиксируется в суставе. Искусственная конечность робота "Кибернетический автомат" должна воспроизводить любое из перечисленных состояний живой ноги. Более строго, при движении каждая нога "автомата" за один шаг должна последовательно проходить через следующие четыре состояния - свободное расслабление, сокращение, растяжение, жесткая фиксация (упор). Эти состояния образуют цикл, который многократно повторяется в процессе ходьбы. Следовательно, минимальный набор функций механической системы шагающего аппарата должен обеспечивать переход конечностей в любое из четырех состояний, а система управления должна обеспечивать указанную последовательность смены состояний каждой конечности и заданный порядок чередования состояний всех конечностей аппарата. Именно таким минимальным набором механических и управляющих функций обладает "Кибернетический привод". Смена состояний "Кибернетического привода" происходит в соответствии с его априорно заданной таблицей переходов. Как следует из таблицы, под воздействием двухразрядного двоичного сигнала, поступающего на вход "привода", на выходе вырабатывается управляющий сигнал, который переводит "привод" в заданное состояние. Соответствие вводных сигналов и выходных состояний определяется конструкцией привода и не может быть изменено в процессе его эксплуатации. Помимо перехода в любое из четырех фиксированных состояний "Кибернетический привод" может управлять непрерывным поворотом искусственной конечности. В частности, если буквой z обозначить выходную переменную, величина которой управляется "приводом", то замкнутое множество S = [z_a, z_b] будет определять связное множество точек, достижимых каждой конечностью "Кибернетического привода". (Здесь z_a и z_b - предельные значения управляемой величины.)

Таблица состояний и кодировка управляющих воздействий привода одной конечности шагающего аппарата 'Кибернетический автомат'

Применение моделей граничных состояний не только оказалось полезным при разработке "Кибернетического привода" (в особенности его таблицы состояний), но и позволяет организовать эффективное управление перемещением шагающего аппарата с любым числом конечностей при произвольной походке (порядке чередования ног). Поскольку число внутренних состояний "Кибернетического привода" невелико, схемы управления оказываются чрезвычайно простыми даже для самых сложных типов походки.

Шестиногие шагающие аппараты

Шестиногие шагающие роботы, по-видимому, являются самой многочисленной из всех когда-либо и где-либо разработанных категорий механизмов, способных перемещаться с помощью искусственных ног. Популярность этих роботов в значительной степени обусловлена тем, что проблемы обеспечения статической устойчивости движущихся шестиногих аппаратов решаются относительно просто по сравнению с другими конструкциями. В настоящее время при проектировании шагающих аппаратов с шестью конечностями исследователей интересуют прежде всего ответы на следующие вопросы: как организовать эффективное управление всеми шестью конечностями шагающего аппарата и как объединить эти методы управления с системами технического зрения и системами распознавания образов, чтобы робот мог автоматически распознавать произвольные препятствия и по возможности плавно перемещаться по неровной поверхности? Кроме того, поскольку шестиногая конструкция робота является, очевидно, наиболее приемлемой с практической точки зрения, ожидается, что помимо преодоления обычных препятствий типа впадин и выступов такие роботы смогут относительно просто справляться и с более сложными задачами, например спускаться и подниматься по лестницам зданий и строительных сооружений.

Одной из проблем, которой уделяется существенное внимание при проектировании мобильных шагающих аппаратов, является уменьшение необходимой мощности источников питания и сокращение затрат энергии. Другими словами, необходимо повысить к. п. д. многоногих механизмов, т. е. уменьшить потребляемую мощность и повысить развиваемую мощность. В самом деле, если учесть, что в общем случае каждая из n конечностей имеет две-три степени подвижности и управление каждой из степеней сопряжено с определенными затратами энергии, то очевидно, что сравнение шагающих и колесных транспортных средств по к. п. д. будет далеко не в пользу первых. В связи с этим, по-видимому, главная цель, к достижению которой должны стремиться исследователи сегодня, заключается в создании экспериментальных шагающих аппаратов, способных на практике продемонстрировать сочетание высоких функциональных возможностей с достаточно большой развиваемой мощностью при малых затратах энергии.

Под руководством Макги была разработана система управления ходьбой шестиногого робота, каждая из конечностей которого приводится в движение с помощью трех электромоторов (всего 18 электромоторов). Наличие диодных мостов и триаков^* в системе управления позволяет задать произвольный сдвиг фаз в работе двигателей и, таким образом, обеспечить реализацию походки любого типа. На рис. 4.35 показаны области достижимости^** отдельных конечностей этого робота. Очевидно, управление перемещением шагающего аппарата должно быть организовано так, чтобы при ходьбе ни одна из конечностей не создавала помех для другой. Естественно, самое простое решение проблемы предотвращения столкновений движущихся конечностей - принципиальное устранение самой возможности столкновений путем выбора границ зон достижимости каждой из ног таким образом, чтобы соседние зоны не имели перекрытий. В случае, представленном на рис. 4.35, границы зон достижимости, при наличии которых гарантируется отсутствие столкновений при любом типе походки, обозначены двумя горизонтальными штриховыми линиями.

^* (Триак - кремниевый двунаправленный управляемый тиристор. - Прим. перев.)

^** (Область, в которой в какой-либо момент времени может находиться данная конечность.)

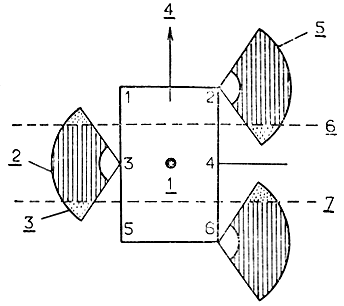
Рис. 4.35. Взаимное перекрытие зон достижимости конечностей шестиногого шагающего аппарата может привести к столкновению конечностей в процессе ходьбы. 1 - центр тяжести; 2 - безопасная область для конечностей; 3 - область возможного столкновения конечности 3 с конечностью 5 (запрещенная область для конечности 3); 4 - направление движения аппарата; 5 - безопасная область для конечности 2; 6 - Передняя граница безопасных областей; 7 - задняя граница безопасных областей. 1, ..., 6 - номера конечностей

Под руководством советского ученого Д. Е. Охоцимского был выполнен цикл работ по исследованию шестиногого педипулятора, способного ориентироваться на местности с помощью однонаправленного сканирующего датчика для измерений расстояний. Последний по своим функциям подобен усикам насекомого. Изучение поведения такого робота при передвижении различными способами на местности с разнообразными препятствиями осуществлялось главным образом моделированием на ЭВМ. Применявшаяся в расчетах на ЭВМ идеализированная модель этого мобильного робота с элементами очувствления показана на рис. 4.36.

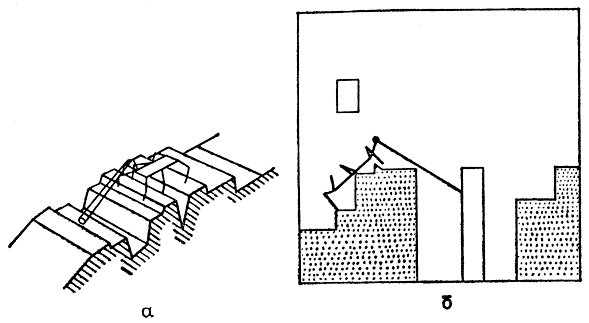
Рис. 4.36. Графическое моделирование движения шагающего аппарата с шестью конечностями. а - преодоление препятствий типа 'произвольная неровность'; б - переход через 'ущелье'

Общий вид еще одного мобильного робота с шестью конечностями, созданного под руководством д-ра Икэда и д-ра Носаки, показан на рис. 4.37. Каждая из конечностей управляется от одного пневматического привода. Экспериментальные исследования этого привода показали, что в тех случаях, когда между "подошвами" робота и полом наблюдается проскальзывание, избежать его и обеспечить плавность перемещения корпуса удается только за счет специальных алгоритмов управления приводами конечностей.

Рис. 4.37. Шестиногий шагающий аппарат с пневматическими приводами конечностей

Как уже отмечалось, потребности в мобильных роботах специального назначения, например в роботах для обслуживания ядерных реакторов или для тушения пожаров и выполнения спасательных работ на пожарах, будут стремительно возрастать. Следует добавить, что, по всей вероятности, эти потребности будут удовлетворяться прежде всего за счет шагающих аппаратов с шестью конечностями. Очевидно, что в соответствии с условиями применения этих роботов первым в списке из важнейших функциональных возможностей должно быть указано умение достаточно быстро спускаться и подниматься по лестницам с различными размерами и частотой ступенек. Поэтому есть основания предполагать, что в ближайшем будущем исследования шестиногих шагающих аппаратов, способных ходить по лестницам, будут развиваться наиболее быстрыми темпами.

Шагающий робот с пятью конечностями

Под руководством Исигава (компании Hitachi) был разработан мобильный робот с пятью конечностями, предназначенный для выполнения операций по обслуживанию атомных электростанций (рис. 4.38). При его разработке особое внимание уделялось обеспечению плавности всех перемещений. Каждая из конечностей этого робота может совершать независимые перемещения вверх-вниз в вертикальной плоскости. "Подошвы" конечностей оборудованы шаровыми колесиками в специальных скользящих оправах. С помощью этих колесиков робот может плавно перемещаться по ровной поверхности^*.

^* (Поэтому данный мобильный робот нельзя считать шагающим в строгом смысле этого слова. Тем не менее он был сконструирован специально для движения по лестницам и справляется с этой задачей лучше любого из известных сейчас "по-настоящему" шагающих роботов. Может быть, появление этого робота позволит углубить или расширить смысл, вкладываемый в понятие шагающие роботы.)

Рис. 4.38. Шагающий робот с пятью конечностями, способный подниматься по лестнице (фирма Hitachi)

Конечности пятиногого робота располагаются в вершинах правильного многоугольника. Устройство каждой из них схематически показано на рис. 4.39, а на рис. 4.40 поясняется, каким образом роботу удается взбираться по ступенькам. Как следует из рисунка, приблизившись вплотную к ступеньке, нога поднимается над ней и разворачивается на 180°. В результате колесо этой ноги оказывается уже на поверхности следующей ступеньки. Хотя сказанное относится к работе лишь одной из ног, все остальные ноги забираются на ступеньку точно так же. В самом деле, после того как первая нога продвинется по поверхности верхней ступеньки на максимально возможное расстояние, одна из четырех остальных ног окажется вплотную прижатой к стенке этой ступеньки. Из этого положения она, подобно первой ноге, поднимается вверх и разворачивается на 180° и вслед за первой ногой размещается на поверхности следующей ступеньки. Таким образом вся тележка постепенно перебирается на новую ступеньку, и описанный процесс повторяется до тех пор, пока не будет достигнута вершина лестницы.

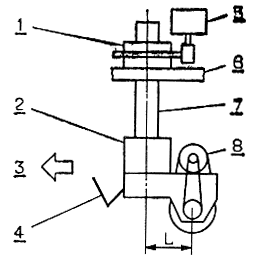
Рис. 4.39. Устройство механической конечности пятиногого шагающего робота. 1 - гайка; 2 - электродвигатель № 2; 3 - направление движения; 4 - датчик касания поверхности; 5 - электродвигатель № 1; 6 - корпус: 7 - болте 8 - электродвигатель № 3

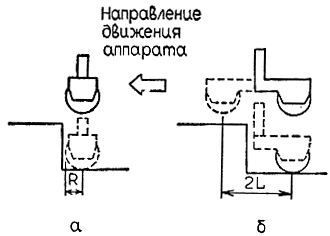
Рис. 4.40. Схема работы конечностей пятиногого шагающего робота при поднятии на одну ступеньку лестницы

При такой конструкции шагающего механизма множество доступных для робота лестниц с различными размерами и частотой ступенек ограничивается размерами "подошвы" конечностей, максимальной высотой, на которую может подниматься каждая из конечностей, а также размерами пятиугольника конечностей. Предположим для определенности, что высота ступеньки равна Н, ее ширина - W, а диаметр окружности, описывающей пятиугольник конечности, и максимальная высота подъема каждой конечности равны соответственно D и L (рис. 4.41). Множество доступных для данного пятиногого робота лестниц определяется диаграммой, приведенной на рис. 4.41, в зависимости от соотношений между высотой ступеньки и высотой подъема ноги и между шириной ступеньки и диаметром D. В данном случае робот, параметры которого соответствуют заштрихованной на диаграмме области, может уверенно спускаться и подниматься по лестницам.

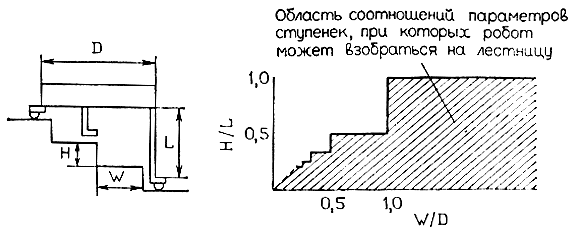
Рис. 4.41. Множество лестниц, доступных для шагающего робота с пятью конечностями, определяется соотношением параметров ступенек с габаритами и максимальной высотой подъема конечностей робота

Шагающий робот с четырьмя конечностями

Как уже отмечалось, все четвероногие животные при движении сохраняют равновесие почти исключительно за счет динамической устойчивости. Однако в случае искусственных шагающих аппаратов походка может быть определена таким образом, чтобы центр тяжести аппарата постоянно находился внутри треугольника, вершинами которого являются конечности, находящиеся на данный момент времени в опорном положении. На практике эта возможность была реализована д-ром Такути из Научно-исследовательского центра проблем механики. Под его руководством был разработан шагающий аппарат с четырьмя конечностями, у которых скорость движения в фазе восстановления подобрана так, что длительность этой фазы втрое меньше длительности каждой рабочей фазы. В результате в данный момент времени лишь одна нога робота находится в воздухе, а корпус опирается на три остальные, сохраняя тем самым статическую устойчивость. Особенности процесса ходьбы этого робота иллюстрируются на рис. 4.42. Показанные на рисунке заштрихованные треугольники (так называемые опорные треугольники) образованы вершинами, которые соответствуют текущим точкам касания опорной поверхности какими-либо тремя из четырех ног робота. Например, в состоянии, соответствующем диаграмме 1, опоры касаются три ноги - А, В, С, а четвертая нога - D, будучи в фазе восстановления, находится в воздухе. Для обеспечения статической устойчивости принципиально важное значение имеет правильный выбор порядка чередования (сдвиг фаз) четырех ног в процессе движения аппарата. В момент времени, отраженный на диаграмме 1, нога В только что коснулась земли и сейчас занимает опорное положение, нога А также касается земли, но находится уже во второй половине своей рабочей фазы, а нога С - еще в первой половине собственной рабочей фазы. Нога D, находящаяся в момент наблюдения в воздухе, быстро заканчивает фазу восстановления, и к моменту времени, которому соответствует диаграмма 2, она уже опускается на землю, переходя в опорное положение. К этому моменту нога А завершила свою рабочую фазу и, оторвавшись от земли, переходит в фазу восстановления; нога В находится в первой половине, а нога С - во второй половине своих рабочих фаз. Аналогично в следующие моменты времени, которым соответствуют диаграммы 3 и 4, в фазу восстановления переходят друг за другом нога С и нога В. При таком порядке чередования ног в любой момент времени, когда одна из ног робота находится в фазе восстановления, центр тяжести аппарата обязательно будет лежать внутри треугольника, образованного тремя ногами, находящимися не в рабочей фазе (опирающимися на землю).

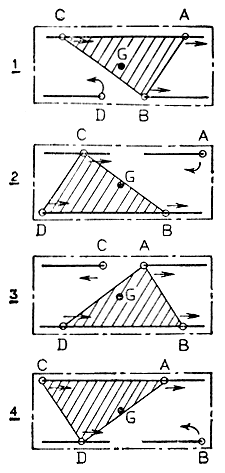
Рис. 4.42. Статическая устойчивость шагающего аппарата с четырьмя конечностями в процессе движения обеспечивается за счет сокращения длительности фазы восстановления в три раза по сравнению с длительностью рабочей фазы. 1, 2, 3, 4 - текущее положение четырех ног; А, В, С, D - амплитуда перемещения ноги вперед-назад; стрелки показывают направление движения каждой ноги

На рис. 4.43 изображено устройство специального механизма, использование которого позволяет в три раза сократить длительность фазы восстановления любой конечности по сравнению с длительностью ее рабочей фазы. Поясним принцип работы этого механизма.

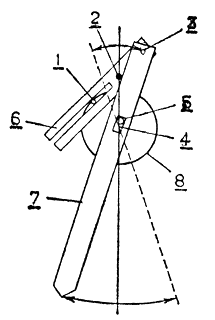
Рис. 4.43. Механизм, обеспечивающий сокращение длительности фазы восстановления конечности шагающего аппарата в три раза по сравнению с длительностью рабочей фазы. 1, 3, 5 - цилиндрические штыри; 2, 4 - неподвижные цилиндрические штыри; 6, 7 - звенья механизма; 8 - поворотный диск

Расположенный на диске штырь 1 вращается с одинаковой скоростью по фиксированной окружности. Когда штырь попадает в некоторую область в нижней части этой окружности, он входит в зацепление с пластиной 6, которая начинает плавно поворачиваться. В результате приходит в движение связанное с ней при помощи штыря 3 звено 7, причем конец этого звена (стопа конечности робота) плавно перемещается вперед по траектории, близкой к прямолинейной. При достижении штыря 1 в верхней части окружности конец пластины 6, на котором расположен штырь 3, начинает двигаться значительно быстрее. Таким образом, в фазе восстановления находящийся в воздухе конец звена 7 перемещается с гораздо большей скоростью, чем в рабочей фазе. Изобретение рассмотренного специального механизма позволило д-ру Икэда построить для своего четырехногого робота исполнительную систему, в состав которой входит всего один электродвигатель. И тем не менее эта система обеспечивает порядок чередования ног, необходимый для поддержания статической устойчивости, а также позволяет добиться плавности перемещения шагающего аппарата.

Как следует из изложенного выше, существуют два основных подхода к построению исполнительных систем, которые могли бы отрабатывать специфический для конечностей шагающих аппаратов цикл, состоящий из фазы поступательного движения и фазы восстановления (рис. 4.29). Первый из них заключается в применении компьютеров для непосредственного управления движением каждой из двух-трех степеней подвижности каждой из конечностей. Его реализация предусматривает создание микропроцессорной системы управления движением шагающего аппарата. Второй подход связан с использованием различных конструктивных хитростей и специализированных механических устройств для решения основных проблем управления циклом ходьбы механическим путем. В только что рассмотренном примере в качестве такого рода устройств применялся механизм, показанный на рис. 4.43.

Каким бы ни был подход, он должен обеспечивать плавное перемещение "стопы" конечности по прямолинейной траектории в фазе поступательного движения. В случае, показанном на рис. 4.43, прямолинейное поступательное движение обеспечивается за счет применения скользящего механизма. Однако при использовании скользящих пар разработчикам, как правило, приходится сталкиваться с проблемами неудовлетворительной точности и малых коэффициентов полезного действия таких механизмов.

За долгую историю развития механики было разработано немало интересных устройств, позволяющих реализовать движение по траектории, приближающейся к прямой линии, без применения скользящих пар. Одним из примеров таких устройств может служить D-driver-механизм, схематически показанный на рис. 4.44; прямолинейное движение достигается за счет соответствующего подбора линейных размеров звеньев.

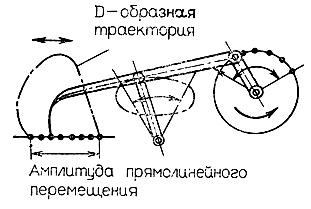
Рис. 4.44. Специализированный D-driver-механизм, обеспечивающий поступательное перемещение стопы конечностей по оптимально возможной траектории

Определенные комбинации конструктивных параметров D-driver-механизма позволяют получить траектории, представляющие большой интерес для разработчиков шагающих механизмов. В частности, на рис. 4.45, а показан пример применения кинематического механизма типа "D-driver" в исполнительной системе шагающего аппарата с шестью конечностями, который был разработан в Научно-исследовательском центре проблем механики под руководством д-ра Абу и д-ра Кинко. Этот механизм состоит из четырех звеньев - СР, PMQ, ОМ и СО, причем длины звеньев удовлетворяют следующему условию: РМ = МО = MQ. Для улучшения сбалансированности исполнительной системы симметрично механизму типа "D-driver" крепится второй такой же механизм (обозначенный точками Q', М', Р', С', Q'). Пара таких механизмов образует исполнительную систему одной конечности робота (в данном случае конечности 3). Собственно ногой в этом механизме является звено, соответствующее на рисунке отрезку прямой QR. Точка R соответствует стопе, которая при ходьбе касается опорной поверхности. Как показано на рисунке, траектория, которую описывает точка Q при почти прямолинейном движении стопы R, по форме напоминает профиль выпуклой линзы. Чтобы стопа R в рабочей фазе совершала полное перемещение (шаг) по квазилинейной траектории, звено 1 должно повернуться на достаточно большой угол (с 90° в исходном положении до 270° в момент окончания рабочей фазы, т. е. на 180°), Используя конструктивные особенности D-driver-механизма, можно механическим способом без особых затрат обеспечить синхронизацию работы ног, необходимую для реализации походки выбранного типа. В частности, в рассматриваемом аппарате с шестью конечностями синхронизация достигается за счет сдвига фаз на 180° между исходным положением звеньев 1 соответствующих ног и вращения этих звеньев с одной скоростью. Другими словами, механизм О, М, Р, С, Q одной ноги работает синфазно с симметричным механизмом ноги, с которой осуществляется синхронизация (этот механизм в конструкции второй ноги занимает то же положение, что и механизм О', М', Р', С, Q' в конструкции первой ноги).

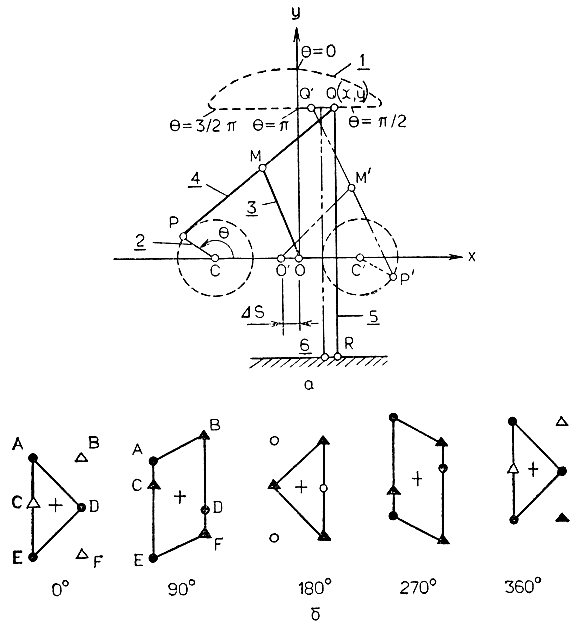
Рис. 4.45. Применение D-driver-механизма в эффективной исполнительной системе для конечностей шестиногого шагающего аппарата. а - модифицированный четырехзвенник Чебышёва в системе управления движением одной конечностью; б - походка шагающего аппарата, реализованная за счет применения модифицированных четырехзвенников Чебышёва в системе управления конечностями. 1 - траектория перемещения точки Q; 2 - звено 1; 3 - звено 2; 4 - звено 3; 5 - конечность; 6 - стопа конечности. Конечности, помеченные одинаковыми знаками ○ или Δ, работают в одной фазе, а конечности, помеченные разными знаками, работают со сдвигом фаз 180°

Применив на практике указанный способ синхронизации работы ног, приводимых в движение с помощью механизмов типа "D-driver", д-р Абу разработал малогабаритный экспериментальный шагающий аппарат с шестью конечностями. Работой всех шести ног этого аппарата управляет всего один электродвигатель. Тем не менее аппарат способен перемещаться в прямолинейном направлении с переменным ускорением. Реализованный тип походки обеспечивает почти полное отсутствие вертикальных колебаний центра тяжести при ходьбе.

Порядок чередования ног для выбранного типа походки поясняется с помощью рис. 4.45. Конечности A, D, Е связаны зубчатым механизмом и движутся при ходьбе синфазно. Другие три конечности - В, С, F - также работают синфазно, однако между конечностями, принадлежащими к различным группам, установлен сдвиг фаз 180°. В моменты времени, когда звено 1 какой-либо ноги поворачивается на угол π/2 или 3/2π (соответствующие звенья остальных ног в этот момент также поворачиваются на π/2 или 3/2π) и на 3/2π (либо на π/2 при сдвиге фаз на 180°), все шесть ног занимают одно положение, находясь на опорной поверхности. Именно поэтому корпус аппарата, который крепится к точкам О-О' каждой ноги, при ходьбе перемещается плавно, практически без вертикальных колебаний. Кроме того, в результате предварительных расчетов параметры звеньев всех кинематических механизмов подобраны таким образом, что при вращении звена 1 каждой из конечностей с одинаковой скоростью линейные скорости конечностей аппарата также одинаковы по абсолютной величине. В результате при ходьбе точки крепления корпуса О-О' каждой из конечностей двигаются синхронно и аппарат не испытывает продольных колебаний. Одна из особенностей конструкции рассматриваемой исполнительной системы заключается в том, что, несмотря на силу реакции опоры, которая возникает при квазилинейном перемещении стопы R (а также точки Q) под действием массы корпуса и перевозимого груза и направлена вверх вдоль звена RQ, величина момента, вращающего звено 1, остается неизменной. Благодаря этому при поступательном движении по достаточно ровной поверхности данный шагающий аппарат по плавности перемещения корпуса и высокому коэффициенту полезного действия приближается к колесным транспортным средствам.

Помимо механизма типа "D-driver" широкое применение в исполнительных системах шагающих аппаратов находят специализированные механизмы еще одного типа - плоскопараллельные, или пантографические, механизмы. Примером таких механизмов может служить устройство, показанное на рис. 3.80. Плоскопараллельные механизмы использовались, в частности, Икэда и Носаки при разработке четырехногого шагающего аппарата с пневматическими приводами.

♦♦♦ Заметим, однако, что обычные пантографические механизмы имеют только две степени подвижности.

На рис. 4.46 показано устройство так называемого цилиндрического пантографического механизма с тремя степенями подвижности - обычный двустепенный пантографический механизм с вращательной степенью подвижности. Впервые этот механизм был применен д-ром Идо в конструкции "Адаптивного манипулятора" (рис. 3.68). Впоследствии аналогичные устройства с небольшими модификациями использовались в конструкциях манипуляторов целого ряда других промышленных роботов. Так, д-р Хиросэ предложил конструкцию трехстепенного кинематического механизма PANTOMEC, который в отличие от цилиндрического пантографа мог совершать боковые прямолинейные перемещения в горизонтальной плоскости. В этом случае, как показано на рис. 4.47, фиксированная ось вращения, вокруг которой первое звено пантографического механизма поворачивается в вертикальной плоскости, проходит через точку R. При повороте первого звена вокруг этой оси точка Q совершает некоторое перемещение в горизонтальной плоскости. Одновременно с точкой Q в том же направлении начинает движение точка Р, которая в итоге проходит расстояние в n раз больше, чем перемещение точки Q. Если учесть, что наряду с плоскими перемещениями точка Q может подниматься и опускаться по вертикали за счет соответствующих движений точки R по вертикальной оси, то окажется, что множество точек, достижимых точкой Q, представляет собой некоторый прямоугольный параллелепипед. Множество точек, достижимых точкой R, также является прямоугольным параллелепипедом. Однако все линейные размеры этого параллелепипеда в n раз превышают соответствующие размеры параллелепипеда для точки Q. Таким образом, данный механизм по своим кинематическим возможностям близок некоторому трехстепенному манипулятору с декартовой системой координат основных движений. Поэтому его также называют декартовым манипулятором.

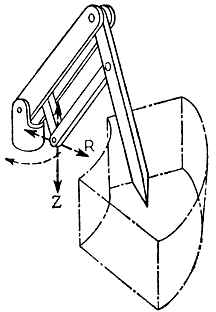
Рис. 4.46. Пантографический механизм с тремя степенями подвижности, работающий в цилиндрической системе координат

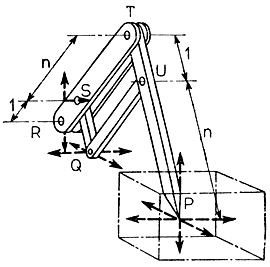
Рис. 4.47. Пантографический механизм с тремя степенями подвижности, работающий в прямоугольной системе координат

Как отмечалось при рассмотрении методов расчета конфигураций манипуляторов, для вычисления обобщенных координат декартовых кинематических механизмов не требуется применения громоздкого аппарата матриц преобразования координат. В этом случае значения обобщенных координат совпадают с координатами текущего положения рабочей точки механизма (например, стопы искусственной конечности). Следовательно, управлять движением декартовых механизмов можно непосредственно с помощью сигналов, задающих требуемые координаты рабочей точки. Это значит, что управление перемещением стопы в какую-либо заданную точку может быть реализовано чрезвычайно просто. С помощью механизмов типа "PANTOMEC" д-р Хиросэ построил шагающий робот с четырьмя конечностями, способный сохранять статическую устойчивость при ходьбе. С помощью расположенных в стопах конечностей тактильных датчиков и датчиков величины наклона опорной поверхности этот робот может взбираться по лестнице, а также преодолевать различные препятствия типа "неровность".

"Двуногие" шагающие роботы

Главное отличие человека от всех других живых существ заключается в качественно более высоком уровне развития центральной нервной системы, в особенности, головного мозга. Это отличие проявляется не только в способности к сложной интеллектуальной деятельности, но и в ряде чисто физических возможностей, свойственных человеку, но не доступных животным. Пожалуй, самой замечательной из таких возможностей является прямохождение, т. е. присущее человеку умение свободно передвигаться на двух ногах. Важнейшим следствием прямохождения стало высвобождение двух передних конечностей, которые в ходе эволюционного развития обрели способность выполнять сложнейшую и искуснейшую работу и превратились в пару человеческих рук. С незапамятных времен умение передвигаться на двух ногах считалось исключительной привилегией и первой отличительной чертой представителей рода человеческого. Неудивительно поэтому, что рукотворные человекоподобные существа, пришедшие к нам из легенд и преданий, а также населяющие страницы современных фантастических романов, независимо от роли, которая им отводится, обязательно передвигаются на двух ногах. Идея прямохождения с давних пор будоражит воображение механиков и конструкторов. И в наше время существует немало ученых, которые посвятили свою исследовательскую деятельность изучению принципов двуногой ходьбы.

Япония одной из первых приступила к работам по созданию роботов, способных передвигаться на двух конечностях, и сейчас именно здесь эти работы ведутся наиболее быстрыми темпами. Главный вопрос, на который ученые ожидают получить ответ в результате изучения основ прямохождения, состоит в следующем: как обеспечить устойчивость (естественно, динамическую устойчивость) механизма, который движется на двух конечностях? Рассмотрим лишь один, но наиболее существенный аспект этой проблемы.

Принцип прямохождения

Изучение принципа прямохождения заключается в выявлении основных механизмов человеческого организма, с помощью которых реализуется возможность устойчивой ходьбы на двух ногах. Изначальная цель таких исследований заключалась главным образом в создании удовлетворительных протезов. Впоследствии, однако, накопленные результаты не только послужили отправной точкой для работ, связанных с построением двуногих роботов, но и оказались весьма полезными на этапах реализации первых кинематических моделей таких роботов.

В США работы по изучению принципов двуногой ходьбы проводятся под эгидой Национального управления по космическим исследованиям и аэронавтике (NASA). Методика этих работ основывается на анализе кинограмм ходьбы человека; съемка производится обычной кинокамерой. В целях упрощения регистрации колебаний центра тяжести в процессе ходьбы к корпусу идущего крепится источник света (лампочка). Чтобы помимо представления о кинематике объекта можно было получать информацию о распределении сил в процессе ходьбы, в опытах использовались различного рода силовые пластины и датчики напряжений, а также проводился анализ отпечатков ног. В связи с прогрессом электронной технологии в последние годы в экспериментах вместо обычной кинокамеры стали применять специализированное устройство слежения, созданное на основе системы технического зрения и управляемое от микрокомпьютера. Такое устройство позволяет проводить наблюдения в большом количестве точек. С его помощью в реальном масштабе времени можно получать непосредственно траекторию движения источников света, прикрепленных к корпусу и суставам конечностей наблюдаемого объекта. В частности, таким способом были получены показанные на рис. 4.48 траектории движения центра тяжести и всех суставов ноги человека при ходьбе. На этом же рисунке для сравнения приводятся траектории, полученные при наблюдении за шимпанзе, перемещающейся на задних лапах. Как следует из рис. 4.48, при ходьбе на двух лапах корпус обезьяны наклоняется далеко вперед, а ноги сильно согнуты в бедренном и коленном суставах.

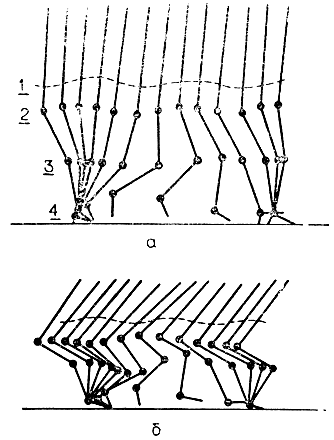
Рис. 4.48. Кинограммы работы ног человека (а) и работы конечностей шимпанзе при ходьбе (б). 1 - центр тяжести; 2 - бедренный сустав; 3 - коленный сустав; 4 - сустав стопы. Шимпанзе перемещается только на задних лапах

Цикл ходьбы человека показан на рис. 4.48, а; для удобства анализа цикл несколько растянут во времени. В момент, когда одна из ног опускается на землю, другая нога отрывается от опорной поверхности и движется вперед по воздуху, оставив при этом вес всего тела на попечении первой, только что опустившейся ноги. Пока вторая нога удерживает тело и обеспечивает его балансировку, первая, продолжая энергично двигаться по воздуху, вытягивается вперед и, закончив шаг, опускается на землю. Сразу после того, как вторая нога коснулась земли, первая нога, которая до этого момента была опорной, начинает приподниматься на носочек и, оттолкнувшись кончиками пальцев, быстро отрывается от опорной поверхности. При движении по воздуху эта нога вытягивается вперед и постепенно выпрямляется так, что стопа, коленный и бедренный суставы лежат практически на одной линии. Выпрямившись, первая нога начинает сжиматься до соприкосновения с опорной поверхностью. Опустившись на землю, она становится опорной, и весь цикл повторяется. Таким образом, реализация двуногой ходьбы связана с решением двух наиболее характерных задач. Во-первых, необходимо, чтобы в процессе ходьбы шагающий аппарат, не падая, мог в течение какого-то времени опираться на одну ногу. Очевидно, чтобы выдерживать нагрузки, возникающие в положении, когда вся масса аппарата приходится на одну ногу, конструкция ноги в целом должна обладать достаточно большой механической прочностью, а приводы - развивать необходимую мощность. Во-вторых, алгоритмы управления стопой, коленным и бедренным суставами, а также углом наклона корпуса, которые обеспечивают то сохранение равновесия всей опирающейся на одну ногу конструкции, то энергичное выполнение шага, оказываются чрезвычайно сложными.

Две указанные проблемы должны также решаться при проектировании любого двуногошагающего аппарата. Как правило, такой аппарат имеет очень сложную механическую конструкцию, состоящую из корпуса, бедренного и коленного суставов и стопы, причем каждый из суставов, стопа и угол наклона корпуса обычно управляются от своих независимых приводов. В большинстве известных двуногих шагающих аппаратов используются приводы электрогидравлического типа.

Конструкции

Самый первый в мире шагающий робот, способный в полном смысле этого слова передвигаться на двух ногах, был разработан в Университете Васэда под руководством д-ра Кадо. Общий вид этого робота показан на рис. 4.49, а на рис. 4.50 представлены кинематические схемы, иллюстрирующие особенности степеней подвижности этого робота.

Рис. 4.49. Двуногий шагающий робот

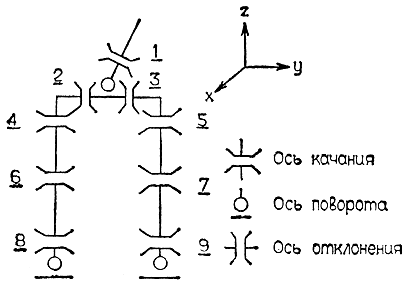
Рис. 4.50. Степени подвижности конечностей двуногого шагающего робота показанного на рис. 4.49. 1 - шарнир наклона корпуса; 2 - правый поясничный шарнир; 3 - левый поясничный шарнир; 4 - правый бедренный шарнир; 5 - левый бедренный шарнир; 6 - правый коленный шарнир; 7 - левый коленный шарнир; 8 - шарнир правой стопы; 9 - шарнир левой стопы

Как следует из рис. 4.50, кинематический механизм робота включает 11 шарниров (обладает 11 степенями подвижности). Среди них: шарниры стопы (2 шт.), шарниры лодыжки (2 шт.), коленные шарниры (2 шт.), бедренные шарниры (2 шт.), поясничные шарниры (2 шт.), шарнир наклона корпуса (1 шт.). Перечисленные шарниры в соответствии с расположением своей оси вращения обеспечивают один из трех типов движения: качание, вращение, отклонение. При качании центр тяжести перемещается поступательно в прямом направлении, при вращении он колеблется влево-вправо, а при отклонении возникает возможность для изменения направления поступательного движения центра тяжести. Движение робота в прямолинейном направлении начинается при согласованной работе шести шарниров, каждый из которых обеспечивает перемещение типа "качание". Когда в результате качания нога полностью приподнимается над полом, в работу вступает шарнир типа "вращение", который поворачивает корпус вперед, чтобы центр тяжести робота тоже переместился вперед. Сразу после этого с помощью шарнира наклона корпуса последний слегка наклоняется влево или вправо. В результате поворота и наклона корпуса и прикрепленного к корпусу груза центр тяжести перемещается таким образом, что вся масса робота перераспределяется на одну опорную ногу. Затем при помощи сустава стопы опорной ноги проводится корректировка положения центра тяжести, в результате которой проекция центра тяжести приходится точно на стопу. При этом обеспечивается сохранение контакта стопы с опорной поверхностью всей плоскостью подошвы. Описанный процесс является симметричным по отношению к левой или правой конечности шагающего аппарата; при ходьбе он полностью повторяется на каждом шаге.

Изменение направления движения достигается за счет работы звеньев поясничной части робота (шарниры типа "отклонение"), при помощи которых нога потихоньку разворачивается в нужную сторону. Максимальный угол поворота ноги за одно движение составляет 15°. Поэтому крутые развороты на большие углы выполняются в результате многократных разворотов ног в пояснице с последующей после каждого разворота балансировкой корпуса.

Общая масса рассматриваемого двуногого робота - 130 кг, а его максимальная грузоподъемность - 30 кг. Очевидно, для того чтобы вся конструкция с грузом могла надежно удерживаться на одной ноге, приводы всех шарниров ноги должны обладать очень большой мощностью. Поэтому при проектировании исполнительной системы шагающего аппарата не оставалось ничего другого, как остановить выбор на электрогидравлических приводах. Рабочая жидкость подается в цилиндры под давлением от внешнего стационарного источника. Таким образом, гидрокомпрессор и электромотор компрессора не увеличивают общую массу шагающего аппарата.

При рассмотренном выше способе передвижения двуногий робот на каждом шаге сохраняет статическую устойчивость. Как отмечалось ранее, такой тип походки называется статическим. Особенности статической походки шагающего аппарата с двумя конечностями иллюстрируются Q помощью рис. 4.51. Как следует из рисунка, когда масса всего робота приходится на одну из ног, центр тяжести робота G₁ лежит внутри четырехугольника A₁B₁C₁D₁, представляющего собой стопу опорной ноги. После того как другая нога, сделав шаг, опускается на землю в диагональном направлении от стопы первой ноги (в этот момент стопа второй ноги занимает положение, обозначенное четырехугольником A₂B₂C₂D₂), масса робота на какое-то время распределяется равномерно между двумя точками опоры. При этом центр тяжести робота G'₁ оказывается внутри многоугольника A₁B₁C₁C₂D₂A₂. На следующем этапе центр тяжести из точки G'₁ перемещается в точку G₂, причем в процессе движения из G'₁ в G₂ он постоянно находится внутри заштрихованного многоугольника. Такое перемещение центра тяжести реализуется путем соответствующего наклона корпуса робота с грузом. После того как движение центра тяжести закончено и он оказался внутри четырехугольника A₂B₂C₂D₂, в работу вступают алгоритмы управления, реализующие отрыв стопы первой ноги (обозначенной четырехугольником A₁B₁C₁D₁) и обеспечивающие сохранение равновесия робота при опоре на вторую ногу. Сделав шаг, первая нога опускается на землю в диагональном направлении от второй ноги (стопа первой ноги занимает положение, обозначенное четырехугольником А₃В₃С₃D₃). На этом завершается один цикл и начинается следующий. Таким образом, в процессе движения данный двуногий робот сохраняет статическую устойчивость в каждом цикле ходьбы.

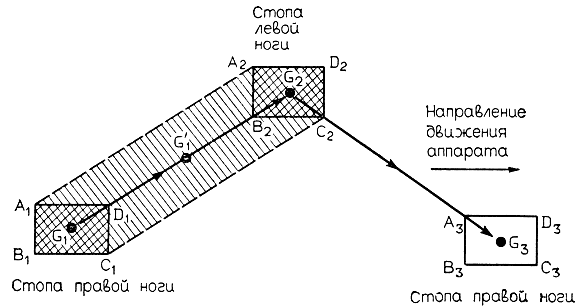
Рис. 4.51. Перемещение центра тяжести двуногого шагающего аппарата при статической походке

Рассмотренный метод управления ходьбой двуногого робота сравнительно прост в реализации. Однако если ограничиться применением только алгоритмов расчета компенсирующих перемещений центра тяжести, то вряд ли удастся добиться требуемой степени плавности перемещения шагающего аппарата. Чтобы понять, как же все-таки это удается человеку, проанализируем еще раз результаты наблюдений за ходьбой человека.

Распределение сил реакции опоры для каждой ноги человека в процессе одного цикла ходьбы графически представлено на рис. 4.52. Как следует из рисунка, в момент, когда правая нога касается опорной поверхности, левая нога, для того чтобы оторваться от земли, развивает максимальное давление на опорную поверхность (первый пик). После того как левая нога, пройдя некоторое расстояние по воздуху, опускается на землю и принимает на себя всю массу тела человека, реакция опоры вторично достигает максимального значения (второй пик). Что касается правой ноги, то графики реакции опоры на эту ногу имеют аналогичный вид, но смещены по фазе на один шаг. В то время, когда реакция опоры на левую ногу увеличивается, реакция опоры на правую ногу начинает пропорционально уменьшаться и становится равной нулю, когда давление левой ноги на землю достигает максимума. Кроме того, нетрудно заметить, что в каждом цикле ходьбы существуют отрезки времени, в течение которых обе ноги одновременно касаются опорной поверхности. Отметим также, что за все время, в течение которого одна из ног находится на земле, реакция опоры, действующая на эту ногу, не остается постоянной, а достигает максимальной и минимальной величины. Минимум реакции опоры на одну из ног достигается за счет направленного вверх импульса, который развивает другая нога при движении по воздуху в высшей точке своей траектории.

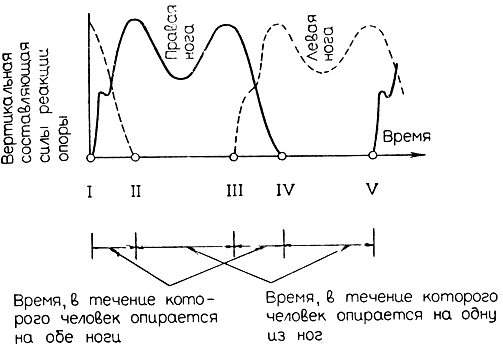
Рис. 4.52. Диаграмма изменения силы реакции опоры, действующей на стопы человека при ходьбе. I - момент опускания правой ноги на землю; II - момент отрыва левой ноги от земли; III - момент опускания левой ноги на землю; IV - момент отрыва правой ноги от земли; V - время, в течение которого человек опирается на обе ноги

Еще одним ключом к пониманию устойчивости и плавности двуногой ходьбы являются данные анализа колебаний центра тяжести человеческого тела в процессе ходьбы. На рис. 4.53, а и б представлены данные наблюдений, выполненных Кадо и Мурата^* методом стереофотосъемки. Как следует из рис. 4.53, а, при ходьбе центр тяжести человека почти не смещается в поперечном направлении. Даже увеличение или уменьшение скорости ходьбы практически не отражается на частоте или амплитуде смещений центра тяжести влево или вправо. Из анализа данных, приведенных на рис. 4.53, становится ясно, что при ходьбе устойчивость человека в отличие от ранее рассмотренного двуногого робота (рис. 4.51) обеспечивается главным образом за счет динамической балансировки.

^* (Технологический университет префектуры Айти.)

Чтобы обеспечить динамическую устойчивость двуногих шагающих аппаратов, Вукобратович предложил так называемый метод "точки с нулевым моментом сил" (ZMP-метод). Сущность управления движением шагающего робота с помощью ZMP-метода заключается в расчете и выполнении компенсирующих смещений корпуса робота таким образом, чтобы в каждый момент времени на поверхности подошвы опорной ноги существовала некоторая точка, для которой равнодействующая сил тяжести и моментов инерции равна 0. Однако выполнение таких расчетов в реальном масштабе времени в течение всего цикла ходьбы требует очень мощных вычислительных средств и оказывается трудно реализуемым на практике. В Университете Васэда под руководством Карисэ был разработан упрощенный метод управления ходьбой с динамической устойчивостью, основанный на принципе ZMP, однако расчет компенсирующих перемещений корпуса проводится только для моментов времени, в которых робот опирается на одну ногу, а при смене ног весь механизм движется подобно висячему маятнику (такой способ перемещения Карисэ назвал нормальной динамической ходьбой).

Рис. 4.53. Траектория перемещения центра тяжести человека при ходьбе. а - смещение центра тяжести в вертикальном направлении (вверх-вниз); б - смещение центра тяжести в горизонтальном направлении, (влево-вправо). Ο - движение со скоростью два шага в секунду; Δ - движение свободным прогулочным шагом; × - движение со скоростью два шага за 1,25 с

В общем случае, для того чтобы управлять динамической устойчивой ходьбой двуногого робота, необходимо составить систему уравнений движения шагающего аппарата, моделью которого, как правило, является некоторый многозвенный кинематический механизм. Обычно такой механизм имеет большое число звеньев и обладает многими степенями подвижности. В результате математическая модель аппарата (система уравнений) оказывается слишком сложной, а ее аналитическое исследование становится практически невозможным. Поэтому первое, что необходимо сделать для реализации управления динамической устойчивостью, это найти какой-либо способ упрощения полных аналитических моделей с учетом специфических особенностей двуногой ходьбы. Одна из чрезвычайно простых для аналитического исследования моделей двуногой ходьбы была предложена д-ром Идо^*. Соответствующая этой модели схема шагающего аппарата показана на рис. 4.54. В данном случае для облегчения анализа приняты следующие, не соответствующие реальности допущения:

^* (Университет префектуры Нагоя.)

● время, в течение которого обе ноги одновременно касаются земли, равно 0;

● длина опорной ноги остается неизменной с момента касания опоры до момента отрыва от нее;

● все движения аппарата совершаются только в сагиттальной плоскости (плоскости, делящей тело человека на правую и левую части), т. е. центр тяжести может перемещаться либо вверх-вниз, либо вперед-назад.

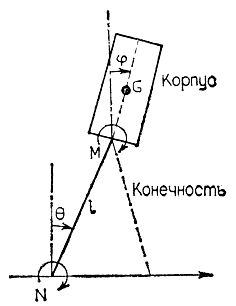
Рис. 4.54. Простейшая модель двуногого шагающего аппарата

Кроме того, предполагается, что стопа касается опорной поверхности только в одной точке, а величина силы трения, возникающей между стопой и полом, достаточна для того, чтобы исключить возможность проскальзывания. Считается, что аппарат приводится в движение только за счет крутящих моментов М и N: первый из них развивается приводом бедренного сустава, а второй возникает под действием силы реакции опоры на стопу. В результате введенных упрощений д-ру Идо удалось провести полное аналитическое исследование движения такого гипотетического аппарата.

Аналитическое описание и анализ движения многозвенного шагающего аппарата с двумя конечностями (рис. 4.55) были выполнены Миядзаки и Аримото. На этот раз основное упрощение было достигнуто за счет отказа от рассмотрения движения робота в пространстве и ограничения задачи плоским двумерным случаем.

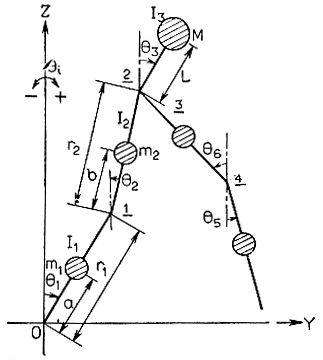
Рис. 4.55. Плоская модель двуногого шагающего аппарата

При аналитическом анализе двуногих шагающих аппаратов для составления уравнений движения этих аппаратов обычно используется принцип Лагранжа. Некоторые из исследователей полагают, что для того, чтобы двуногий механизм мог перемещаться столь же плавно, как и человек, конструкция этого механизма должна в точности воспроизводить строение человеческой ноги. Однако известно, что при достаточном навыке можно очень плавно перемещаться с помощью простейших ходулей. Сосредоточив свое внимание на анализе принципов ходьбы на ходулях, Ситаяма и Мицура^* разработали двуногий аппарат, который способен переступать на месте с ноги на ногу не падая (двуногий переступающий аппарат). Алгоритмы управления, обеспечивающие устойчивость аппарата в вертикальном положении, основаны на аналитическом исследовании уравнений движения этого переступающего робота. Конструкция реализованного под руководством Ситаяма двуногого шагающего на ходулях робота показана на рис. 4.56. Как следует из рисунка, робот управляется от трех электроприводов (фактически используются четыре электромотора, так как привод корпуса состоит из двух электромоторов). Два электродвигателя, обозначенные цифрами I и II, управляют перемещениями вращательного типа (уменьшением или увеличением расстояния между точками опоры двух ног), а два электродвигателя, помеченные цифрой III, управляют движениями типа качания. Направления осей вращения и качания показаны на рис. 4.56. В исходном положении робот опирается на обе ноги. Если в этом положении вращающий момент, развиваемый двигателем I (или двигателем II), превысит некоторое установленное значение, то правая (или левая) нога оторвется от пола и будет находиться в воздухе в течение некоторого, заранее установленного интервала времени. В результате попеременной работы двигателей I и II робот топчется на месте, поднимая то правую, то левую ногу. Если величина вращающих моментов и период чередования двигателей поддерживаются неизменными, то похожий на обыкновенные ходули шагающий робот будет сохранять устойчивое вертикальное положение в течение всего процесса переступания с ноги на ногу.

^* (Токийский университет.)

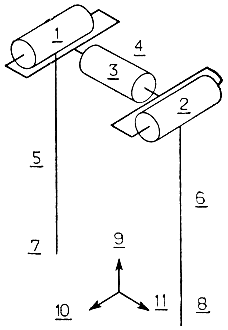
Рис. 4.56. Устройство двуногого робота, перемещающегося на ходулях. 1 - электромотор I; 2 - электромотор II; 3 - электромотор III; 4 - корпус; 5 - левая нога; 6 - правая нога 7 - стопа левой ноги; 8 - стопа правой ноги; 9 - вертикальная ось; 10 - ось наклона; 11 - ось качания

При составлении системы уравнений, аналитически описывающей характер движения робота на ходулях, использовалась упрощенная модель, показанная на рис. 4.57. Когда робот опирается на одну ногу, уравнения движения, полученные для этой модели, имеют следующий вид:

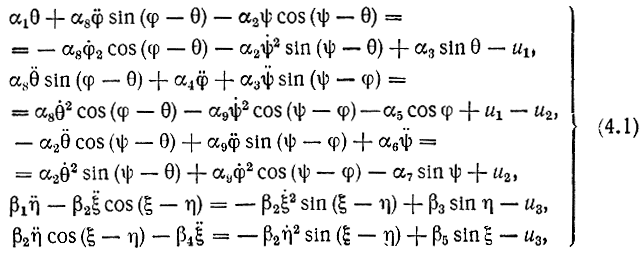
где

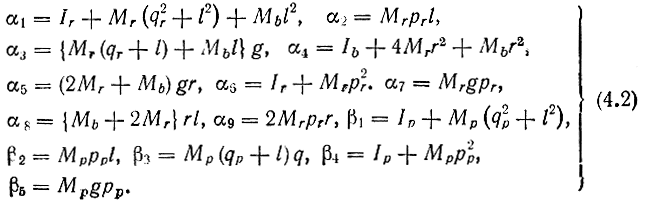
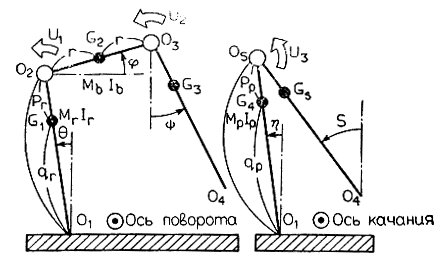
Рис. 4.57. Упрощенная модель двуногого робота, перемещающегося на ходулях

При разработке реальных алгоритмов управления переступающим роботом Ситаяма провел линеаризацию всех уравнений данной системы. Определив цикл ходьбы как чередование последовательности состояний: опора на одну ногу → смена опорных ног → опора на другую ногу, он представил "смену опорных ног" в виде "черного ящика", а конфигурации, которые робот имеет в самом начале и в самом конце этого состояния, в виде неизвестных функций. Рассматривая эти функции в качестве условий сопряжения двух систем уравнений, каждая из которых описывает состояние робота при опоре на одну из ног, он получил полное математическое описание каждого из состояний цикла ходьбы в виде соответствующей системы уравнений. В результате решения этих систем Ситаяма получил алгоритм непрерывного управления процессом переступания, несмотря на то что этот процесс по своей сути является дискретным.

Выше были рассмотрены лишь некоторые наиболее впечатляющие результаты теоретических и экспериментальных работ по созданию двуногих шагающих роботов. Но даже этого вполне достаточно, чтобы прийти к следующему выводу: двуногие шагающие роботы с динамическим управлением устойчивостью перестали быть объектом внимания писателей-фантастов. Уже сейчас разработано несколько вполне удовлетворительных моделей шагающих аппаратов с двумя конечностями, и имеются все основания полагать, что в скором времени это направление робототехники достигнет своего апогея.