3.3. Идентификационный подход к адаптивному программному управлению

Для синтеза законов управления ПД, обеспечивающих наперед заданное качество переходных процессов, достаточно точно знать динамическую модель РТК и ПД. Если это условие выполнено, то проблема синтеза может быть решена, например, с помощью законов управления вида (3.12). Однако в действительности динамическая модель РТК известна в лучшем случае с точностью до вектора параметров ξ и постоянно действующих возмущений π. Эти неопределенные величины удовлетворяют лишь общим ограничениям (3.4) и (3.5) и могут принимать любые значения внутри заданных ограниченных множеств Q_ξ и Q_π.

Для компенсации возникающей неопределенности необходимо, чтобы система управления самостоятельно отыскивала недостающую информацию в процессе адаптации РТК к фактической обстановке. В этом случае появляется принципиальная возможность получить такое качество переходных процессов, которое достижимо лишь при точном знании уравнения динамики (3.1).

Компенсацию априорной неопределенности и оценивание неизвестных величин можно осуществлять по-разному. В теории адаптивных систем наиболее распространены два подхода, которые будем условно называть "идентификационным" и "безыдентификационным". Суть идентификационного подхода заключается в воздействии на двигательную систему РТК определенными "тестовыми" управляющими воздействиями и в фиксации с помощью информационной системы характеристик реального движения, порожденного этими "пробными" воздействиями. В результате такого "зондирования" РТК получается система уравнений относительно неизвестных параметров ξ. Решая эту систему алгебраических уравнений тем или иным методом, можно идентифицировать неизвестные параметры. После этого найденные оценки можно подставить в синтезированные законы управления, например в законы (3.12).

Процесс идентификации неизвестных параметров целесообразно совместить с процессом управления. При этом управление служит двум целям. С одной стороны, оно выступает как средство изучения динамики РТК путем текущей идентификации его параметров, с другой - закон управления, использующий идентифицированные параметры, обеспечивает желаемый характер переходных процессов при отработке ПД. В этом проявляется дуальность управления с идентификацией.

Дуальное управление представляет собой разновидность адаптивного управления. Для него характерно, что процесс автоматической идентификации параметров совмещен (или чередуется) с процессом собственно управления. При этом управление направлено как на "зондирование" динамики РТК, так и на осуществление заданного ПД. Благодаря активному накоплению информации путем "зондирования" оказывается возможным определить неизвестные параметры. Для синтеза алгоритмов идентификации нужно прежде всего выбрать критерий качества идентификации.

Проиллюстрируем высказанные соображения на примере простейшей схемы адаптивной идентификации параметров динамической модели РТК на основе настраиваемой модели. Предположим, что функция F в уравнении (3.1) линейна по ξ. Наряду с уравнением динамики (3.1) с неизвестными параметрами ξ рассмотрим уравнение настраиваемой модели

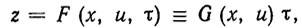(3.21)

где τ- вектор параметров модели, играющий роль оценок неизвестного вектора ξ, а z - вектор выходных переменных модели, трактуемый как оценка (или прогноз) вектора ẋ.

Настройка параметров τ модели (3.21) производится в силу некоторого алгоритма, который нужно построить исходя из заданного критерия идентификации. При этом оценки z вычисляются согласно (3.21) по заданному (тестовому) управлению u, измеренному текущему состоянию х и сформированной оценке τ.

Идентификацию параметров можно осуществлять по "выходам" настраиваемой модели (3.21). Это значит, что параметры τ модели z должны выбираться так, чтобы выход модели z был, по возможности, наилучшей оценкой измеряемого "выхода" ẋ динамической модели. В качестве показателя качества идентификации оценки на интервале времени [t₀, t_T] возьмем интегральную квадратичную ошибку

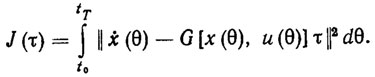(3.22)

Этот показатель, связывающий "выходы" модели z и скорость изменения вектора состояний х, особенно удобен в том случае, когда параметры | не фиксированы, а дрейфуют по неизвестному закону. В этом случае целесообразно рассматривать скользящий интервал идентификации, для которого t₀=t, t_T=t+Т.

Необходимым и достаточным условием минимума показателя (3.22) является равенство нулю градиента функции J(τ). Отсюда непосредственно получаем линейное алгебраическое уравнение относительно настраиваемых параметров τ:

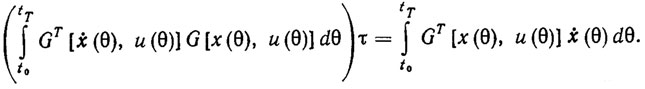(3.23)

Идентификация неизвестных параметров ξ сводится к решению уравнения (3.23).

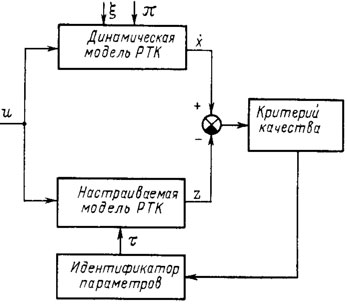
Рис. 3.1. Схема адаптивной идентификации динамической модели РТК

Описанная схема адаптивной идентификации представлена на рис. 3.1. Она привлекательна своей простотой. Однако ей присущ ряд недостатков.

Во-первых, система "идентификационных" уравнений может оказаться плохо обусловленной, а значит, непригодной для точной идентификации параметров ξ. Во-вторых, для фактического решения уравнения (3.23) в сложных случаях может потребоваться значительное время. Такое запаздывание в идентификации недопустимо, если искомые параметры дрейфуют непредсказуемым образом. В-третьих, требование простоты реализации приводит к классу рекуррентных алгоритмов идентификации. Однако эти алгоритмы (типа алгоритма Качмажа или алгоритма "полоска" [132]) сходятся медленно и, следовательно, также приводят к большому времени идентификации. Наконец, реализация рассмотренной схемы идентификации параметров требует специальных средств для измерения или оценивания вектора состояний х и его производной ẋ, что не всегда осуществимо с приемлемой точностью.

Следует отметить, что алгоритмы самонастройки модели (3.21), основанные на минимизации показателей качества (3.22), вообще говоря, не обеспечивают точной идентификации. Они гарантируют лишь близость выходов модели z и ẋ, т. е. решают задачу функциональной идентификации по "выходу". Для точной идентификации целесообразно исходить из иных, сугубо "идентификационных" критериев качества. Наиболее естественными показателями точности идентификации являются функционалы, явно зависящие от параметрических возмущений ω (t) =ξ (t)- τ(t). Примерами могут служить локальный и интегральный показатели:

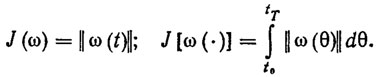(3.24); (3.25)

В работах [107, 109] предложен широкий спектр рекуррентных и много шаговых алгоритмов идентификации, параметры которых выбираются из условия локальной оптимальности показателя (3.24). Эти алгоритмы относятся к классу градиентных алгоритмов решения идентификационных неравенств вида

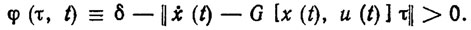(3.26)

Среди них нужно особо выделить рассматриваемый ниже оптимальный много шаговый алгоритм "с полной памятью". Этот алгоритм гарантирует точную идентификацию неизвестных параметров ξ, причем число его шагов не превышает размерности пространства настраиваемых параметров [109].

Концепция дуального управления исходит, по существу, из постулата, что для эффективного управления нужно уметь идентифицировать динамическую модель РТК. Первоначально эта концепция зародилась в теории стохастического управления [101, 136]. Здесь принцип дуальности оказался особенно плодотворным, так как позволил "увязать" результаты классической теории управления с методами стохастической аппроксимации и оценивания. Важную роль дуальное управление сыграло и в становлении теории адаптивных систем.

Однако постепенно было осознано, что точная идентификация не является необходимым условием эффективного управления. Было четко установлено [101, 107, 132], что для успешного управления вовсе не требуется детально изучать динамические свойства объекта управления. На справедливость этого тезиса наводят и физиологические соображения: управляя рукой, мозг отнюдь не утруждает себя точной идентификацией массы или моментов инерции предмета, которым рука манипулирует.

Существуют и более веские доводы, свидетельствующие об ограниченности, а в ряде случаев непригодности концепции дуального управления в робототехнике. Один из них - трудоемкость и сложность осуществления точной идентификации - уже обсуждался выше. Другой связан с тем, что в ряде конкретных задач точная идентификация принципиально невозможна. К числу таких задач относятся, например, все задачи, в которых действуют неконтролируемые возмущения. В этих задачах движения РТК описываются уравнением (3.1), зависящим от постоянно действующих возмущений π (t). Для решения таких задач, особенно характерных для ГАП, приходится опираться на какие-то иные, "не идентификационные" принципы адаптации. Перейдем к рассмотрению этих принципов и реализующих их алгоритмов.