3.4. Концепция алгоритмического конструирования адаптивных систем программного управления

Важнейшей чертой адаптивного программного управления является наличие некоторого алгоритма целенаправленной настройки параметров закона управления в процессе отработки ПД. По существу этот алгоритм представляет собой активный поиск недостающей информации (обучение) и коррекцию закона управления (адаптация) в соответствии с новой информацией, поступающей от системы "очувствления" РТК в ходе управления. Поскольку для высококачественного управления вовсе не требуется точно знать все параметры и условия эксплуатации РТК, можно отказаться от описанного выше идентификационного подхода.

Перейдем к описанию общей схемы алгоритмического синтеза законов адаптивного программного управления, гарантирующих желаемый характер переходных процессов при осуществлении заданного ПД в не детерминированных и изменяющихся производственных условиях. Специфические особенности динамической модели РТК позволяют разделить сложную задачу алгоритмического синтеза адаптивного управления ПД на две самостоятельные задачи.

Первая задача заключается в аналитическом синтезе идеального (не адаптивного) закона управления, обеспечивающего желаемый переходный процесс в предположении, что параметры ξ уравнения динамики (3.1) полностью известны, а возмущения π отсутствуют. Методы и алгоритмы решения этой задачи в различных ее формах (стабилизация ПД, оптимальное терминальное управление и самонаведение) подробно рассмотрены в работах [89-91, 107, 112, 113, 119].

Вторая задача - это синтез алгоритмов адаптивной настройки (самонастройки) параметров законов управления, полученных в результате решения первой задачи. Методы синтеза алгоритмов самонастройки, представляющие основной интерес для адаптивного управления РТК, излагаются в следующем параграфе.

Конкретизируем общую схему решения сформулированных задач с учетом специфических особенностей динамики РТК. С этой целью сначала синтезируем по заданному ПД х_p(t) идеальный (не адаптивный) закон управления, обеспечивающий желаемый характер переходных процессов. Семейство приемлемых законов управления ПД описывается формулой (3.12). Реализация любого закона управления из этого семейства требует точного знания вектора параметров ξ. Однако, как отмечалось выше, эти параметры обычно неизвестны, поэтому синтезированные законы управления вида (3.12) заданы, по существу, с точностью до параметров ξ.

В этих условиях неопределенности закон управления ПД должен быть адаптивным, т. е. должен осуществлять самонастройку параметров. Будем строить адаптивный закон управления в виде

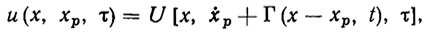(3.27)

где τ= х (t) -текущая оценка неизвестного вектора параметров ξ, определяемая с помощью алгоритма адаптации (3.15).

Эффективность адаптивного программного управления (3.27) в значительной степени зависит от алгоритма адаптации. Выбор этого алгоритма должен осуществляться исходя из единых требований, предъявляемых к процессам управления и адаптации в РТК. Важнейшим из требований является быстрое затухание параметрических возмущений, создающее предпосылки для фактической обработки ПД с заданной точностью.

Уточним понятие цели управления в условиях неполной информации. Система управления РТК должна гарантировать желаемый характер переходных процессов, должна привести к этому несмотря на имеющуюся неопределенность. Поэтому цель адаптивного управления удобно формулировать в терминах свойств переходных процессов. При этом формализация и конкретизация цели управления зависит от решаемой технологической задачи или режима эксплуатации РТК. Так, в задаче адаптивной стабилизации ПД целью управления является обеспечение желаемого характера ПП, гарантирующего асимптотическую устойчивость ПД. Тем самым обеспечивается отслеживание ПД с заданной точностью ε, т. е. выполняется целевое условие (3.16). В задаче адаптивного терминального управления цель управления состоит в достижении наперед заданного состояния х₁ за заданное время технологической операции Т = t_T-t₀, т. е. должно выполняться целевое условие вида (3.17).

Важно подчеркнуть, что названные цели управления ввиду не стационарности и неопределенности условий эксплуатации РТК должны достигаться для любых возможных значений неизвестных параметров ξ и возмущения π из класса неопределенности {Q_ξ, Q_π}. Если система управления, реализующая закон управления (3.27) и алгоритм адаптации (3.15), сконструирована так, что цель управления достигается для любых неизвестных параметров ξ и возмущений π из заданного класса неопределенности, то будем говорить, что РТК адаптивен в этом классе. Поскольку класс неопределенности, задаваемый информационными ограничениями (3.4) и (3.5), может быть практически любым, речь идет по существу об адаптации в широком смысле.

Проблема синтеза алгоритмов адаптации тесно связана с проблемой контроля качества переходных процессов в ходе управления. Для формализации функции контроля введем критерий качества адаптации. К сожалению, указать универсальный критерий, охватывающий с единых позиций все практически интересные случаи, весьма затруднительно. Поэтому ограничимся примерами наиболее характерных критериев качества, хорошо приспособленных к задачам адаптивного программного управления РТК.

Критерии качества адаптации целесообразно задавать в форме эстиматорных неравенств (3.13), связывающих состояния, управления и настраиваемые параметры. Эти вспомогательные неравенства должны обладать тем свойством, что из их выполнения следует достижение цели управления. Среди различных типов эстиматорных неравенств особое значение имеют неравенства вида [107, 111]:

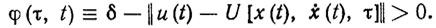(3.28)

Эти неравенства замечательны тем, что при τ= ξ и π=0 они разрешимы с "запасом" δ>0. Кроме того, обычно или выпуклы. Последнее имеет место для многих типов динамических моделей РТК, для которых функция U линейна по третьему аргументу, т. е.

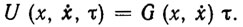(3.29)

Процесс адаптации с критерием качества (3.28) сводится к поиску решения системы эстиматорных неравенств. Это соображение наводит на мысль о том, что в качестве алгоритмов адаптации можно использовать соответствующие модификации алгоритмов выпуклого программирования. Значительный интерес представляют также разного рода рекуррентные алгоритмы вида (3.15), обладающие свойством конечной сходимости [109, 132]. В конкретных задачах адаптивного управления с идентификацией удобны эстиматорные неравенства вида (3.26). Легко видеть, что эти неравенства также выпуклы и разрешимы с "запасом" δ >0 при τ= ξ и π=0. Для их решения опять-таки применимы соответствующие модификации алгоритмов выпуклого программирования, которые выступают здесь как алгоритмы адаптивной идентификации неизвестных параметров.

Проверка эстиматорных неравенств (3.26) и (3.28) требует измерения (или оценивания) не только текущего состояния РТК, но и его производной ẋ. Однако на практике измерение ẋ с высокой точностью трудно осуществимо. Чтобы избавиться от этого ограничения, можно перейти к эстиматорным неравенствам интегрального типа [107, 111]:

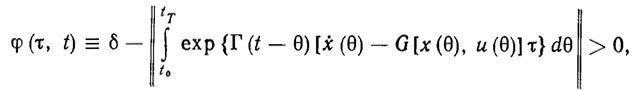
где Г - некоторая устойчивая матрица размерности n*n, входящая в закон управления (3.27). Очевидно, что проверка неравенств (3.29) уже не требует измерения ẋ. По этой причине и алгоритмы адаптации, синтезированные как алгоритмы решения эстиматорных неравенств, не зависят от ẋ.

Характерной особенностью задачи синтеза адаптивного программного управления является то, что в каждый момент времени t известно (или может быть вычислено) текущее значение эстиматорной функции φ [τ(t),t], но не будущее ее значение, которое зависит от будущих оценок и управлений. В свою очередь, оценки τ(t) в каждый момент времени t вычисляются согласно алгоритму адаптации по информации о текущих и, возможно, предыдущих значениях эстиматорной функции. Таким образом, в рассматриваемой задаче адаптация сводится, по существу, к решению заранее не заданных эстиматорных неравенств. Текущий контроль за выполнением этих неравенств производится на основе сигналов обратной связи, формируемых информационной системой РТК.

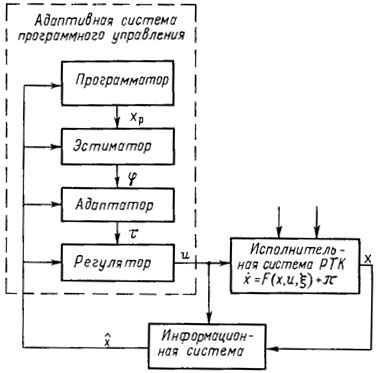
Рис. 3.2. Структурная схема адаптивного программного управления РТК

Знание структуры закона управления ПД (3.27) и синтез подходящего алгоритма адаптации в виде или (3.15) позволяет считать задачу алгоритмического конструирования адаптивного программного управления решенной до конца. В самом деле, если РТК будет снабжен необходимыми датчиками сигналов обратной связи и системой автоматического управления, реализующей синтезированные алгоритмы построения ПД и законы адаптивного управления, то требуемое ПД будет фактически отрабатываться в изменяющихся производственных условиях, причем характер переходных процессов будет близок к желаемому.

Структурная схема адаптивной системы программного управления РТК представлена на рис. 3.2. Эта схема включает в себя следующие иерархически связанные функциональные модули [107]:

1. программатор - модуль построения и оптимизации ПД;
2. эстиматор - модуль оценки качества переходных процессов;
3. адаптатор - модуль самонастройки параметров закона управления.
4. регулятор - модуль формирования закона управления ПД.

Данная схема отражает описанную выше концепцию алгоритмического конструирования адаптивных систем программного управления РТК. Поскольку гибкие алгоритмы программирования и адаптивные задачи управления РТК достаточно сложны, то для их реализации целесообразно применять современные быстродействующие ЭВМ и микропроцессоры.