3.5. Непрерывные алгоритмы самонастройки

Характерным признаком адаптивных систем программного управления РТК является высокоразвитая способность самонастройки к непредсказуемым изменениям внутренних характеристик и внешних условий. Самонастройка закона управления (регулятора) осуществляется с помощью алгоритмов адаптации (адаптатор а).

В теории адаптивных систем разработано большое число различных алгоритмов адаптации 183, 101, 107, 109, 132, 136, 142]. Среди них можно выделить довольно широкий класс непрерывных алгоритмов самонастройки. Отличительной чертой этого класса является то, что оценки τ неизвестных параметров ξ в законе управления (3.27) определяются здесь как решение некоторого дифференциального уравнения адаптации.

Рассмотрим общий подход к синтезу и анализу качества непрерывных алгоритмов самонастройки, основанный на использовании так называемых функций Ляпунова [12, 31, 132]. Первоначально такой подход возник в теории беспоисковых самонастраивающихся систем и нашел применение при синтезе самонастраивающихся автопилотов [3, 132, 136]. Предлагаемый метод самонастройки основан на принципе скоростной адаптации и ориентирован на задачи адаптивной стабилизации ПД^*. Согласно этому методу алгоритм самонастройки синтезируется в виде дифференциального уравнения адаптации

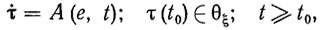(3.30)

где е = х (t)-х_p(t) - переходной процесс; А - оператор адаптации, который нужно сконструировать так, чтобы адаптивное управление (3.27) и (3.30) обеспечивало асимптотическую устойчивость ПД х_p (t).

^* (Принцип скоростной адаптации и основанные на нем непрерывные алгоритмы самонастройки предложены в статье А. В. Тимофеева "Синтез адаптивных регуляторов с помощью функций Ляпунова". - ДАН СССР, т. 274, № 2, 1985, с. 276 - 279. )

Идея синтеза алгоритма самонастройки на основе принципа скоростной адаптации заключается в следующем. Зададим на переходных процессах е и параметрических возмущениях о> положительно-определенную функцию Ляпунова V (е, ω) с отрицательно-определенной заданной производной W (е, ω) и найдем оператор адаптации А из условия:

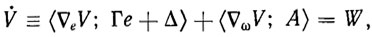(3.31)

где 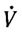- производная функции V(e, ω) по t вычисленная в силу уравнений динамики (3.1); Δ_eV - градиент функции V (е, ω) по е; А = F (х, u, ξ) - F (х, u, τ); Δ _ωV - градиент функции

((е, ω) по ω; (·, ·) - символ скалярного произведения векторов.

Разрешая уравнение (3.31) относительно оператора А и подставляя его в (3.30), получим семейство непрерывных алгоритмов самонастройки, зависящих от выбора функции Ляпунова V и ее производной W. Конкретизируем этот выбор и синтезируем соответствующие алгоритмы самонастройки для случая, когда функция F в уравнении динамики РТК (3.1) линейна по третьему аргументу, т. е. имеет место (3.21).

Зададим функцию Ляпунова V и ее производную в виде

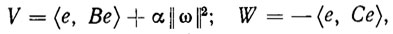(3.32)

где α - положительное число; С - заданная положительно определенная постоянная матрица; В - матрица, определяема как решение уравнения Ляпунова

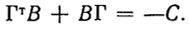(3.33)

Тогда алгоритм самонастройки (3.30) примет вид

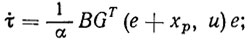(3.34)

он обеспечивает асимптотическую устойчивость ПД. Следовательно, по прошествии некоторого времени переходного процесса t_p будет выполнено целевое условие (3.16).

Зададим теперь скорость изменения функции Ляпунова (3.32) в виде W=-<е, Се>-|| Δ||². Тогда алгоритм самонастройки примет вид

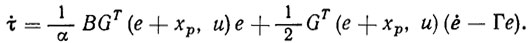(3.35)

Этот алгоритм в сочетании с законом управления (3.27) обеспечивает не только асимптотическую устойчивость ПД, но и асимптотическую идентификацию вектора неизвестных параметров ξ, т. е. справедливо соотношение (3.20).

Недостатком алгоритма (3.35) по сравнению с алгоритмом (3.34) является то, что для его реализации нужна обратная связь не только по вектору состояний РТК х, но и по его производной х. Организация такой обратной связи наталкивается на трудности. Однако в ряде случаев дело сводится к подключению дополнительных датчиков. Так, при адаптивном управлении РТК с моментными двигателями нужно использовать помимо обычных датчиков управляемых координат и скоростей их изменения еще и датчики ускорений (акселерометры).

Рассмотрим другой метод самонастройки, специфика которого заключается в том, что на этот раз дифференциальное уравнение адаптации (3.14) синтезируется исходя из требования решения эстиматорных неравенств (3.13). Алгоритм самонастройки в этом случае имеет вид [42]:

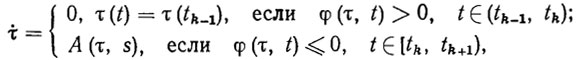(3.36)

где t_k, k = 1, 2, ... - первый момент нарушения эстиматорных неравенств (3.13) на k-u интервале самонастройки [t_k, t_k+1). За интервалом самонастройки следует интервал стабилизации ПД, на котором в соответствии со схемой алгоритма (3.36) τ(t)= τ(t_k+1) Затем вновь наступает интервал самонастройки, в течение которого т определяется как решение дифференциального уравнения адаптации (3.36) при начальном условии τ(t_k+2)= τ(t_k+1) т. д.

Синтез алгоритма самонастройки вида (3.36) сводится к конструированию оператора адаптации А так. чтобы при любой начальной оценке τ(t₀) из множества Q _ξ выполнялись эстиматорные неравенства (3.13), начиная с некоторого конечного момента времени t_r. При этом, очевидно, оценка τ "заморозится": τ (t)= х (t_r) при всех t >t_r.

Основная идея синтеза (3.36) заключается в конструировании специальной функции Ляпунова по заданной ее производной, которая определяется видом эстиматорной функции φ. Такой подход, реализующий, по существу, принцип скоростной адаптации по отношению к алгоритму самонастройки вида (3.36), обладает некоторыми преимуществами по сравнению с традиционными методами, в которых структура функций Ляпунова выбирается заранее.

Зададим на интервалах самонастройки функцию Ляпунова V и ее производную W в виде

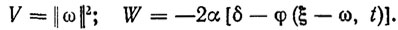(3.37)

Вычисляя производную V в силу (3.36) и учитывая (3.29) и (3.37), получим оператор адаптации

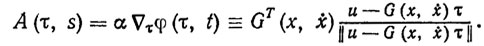(3.38)

Обозначим через θ_k длительность k-го интервала самонастройки, а через r - номер последнего такого интервала. Тогда общее время μ, затраченное на адаптацию, оценивается соотношением

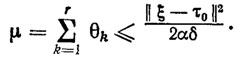(3.39)

Описанный метод позволяет синтезировать и другие алгоритмы самонастройки, обладающие заданными свойствами (например, не требующие измерения ẋ). Для этого нужно только соответствующим образом сконструировать эстиматорные неравенства (3.13), функцию Ляпунова и ее производную.

Реализация синтезированных непрерывных алгоритмов самонастройки сводится к интегрированию (в натуральном масштабе времени) дифференциальных уравнений адаптации. Эта вычислительная операция может быть осуществлена как на аналоговых, так и на цифровых ЭВМ.