3.6. Рекуррентные алгоритмы адаптации

При цифровой реализации адаптивных систем программного управления РТК значительный интерес представляют дискретные алгоритмы адаптации вида (3.15). Рассмотрим основные особенности таких алгоритмов и прежде всего - рекуррентных алгоритмов.

Важнейшим требованием, предъявляемым к дискретным алгоритмам адаптации, является конечность времени адаптации. Именно это свойство отличает описываемый класс алгоритмов от многих известных алгоритмов адаптации, для которых трудно и, как правило, невозможно указать необходимое время "обучения" [101]. Вследствие этого, как отмечается в работе [101], для таких алгоритмов адаптации "оценка момента времени, начиная с которого целевое неравенство будет выполнено, не может быть дана в общем случае". Что же касается рассматриваемого класса конечных алгоритмов, то для них удается оценить не только общее время адаптации, но и момент окончания переходных процессов. Эти оценки играют важную роль при автоматизированном проектировании и расчете параметров адаптивных систем программного управления РТК.

Временем адаптации μ называется множество всех тех заранее неизвестных моментов времени, для которых эстиматорные неравенства (3.13) нарушены на траектории алгоритма адаптации [111]. Для дискретных алгоритмов вида (3.15) конечность времени адаптации обеспечивается конечностью числа коррекций. Обозначим это число через r. Тогда для времени адаптации справедлива следующая оценка:

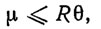(3.40)

где θ - время, затрачиваемое на одну коррекцию, т. е. время вычисления новой оценки τ_k+1 по старой оценке τ_k в соответствии с алгоритмом (3.15). Очевидно, что чем больше быстродействие адаптатора, реализующего алгоритм (3.15), тем меньше θ.

Для дискретного алгоритма (3.15) с конечным временем адаптации (3.40) существует момент времени t_r, начиная с которого эстиматорные неравенства (3.13) будут все время выполнены. После этого момента коррекции прекратятся, а оценка τ_r, полученная на последнем шаге алгоритма "заморозится". Отсюда следует, что система управления РТК, реализующая закон управления ПД(3.27) и конечный алгоритм адаптации вида (3.15), самонастраивается на точное отслеживание ПД после конечного числа коррекций.

Дискретные алгоритмы адаптации вида (3.15) помимо требования конечности времени адаптации должны удовлетворять еще ряду условий. С практической точки зрения весьма важно, чтобы эти алгоритмы были оптимальными в смысле подходящего критерия качества и обладали наибольшей скоростью сходимости, т. е. наименьшим числом коррекций. Большое значение имеет также простота алгоритма адаптации. Это значит, что вычисление оператора адаптации А в алгоритме (3.15) должно требовать, по возможности, минимального числа операций и памяти.

Требования простоты реализации и экономии памяти цифровой системы управления РТК накладывают дополнительные ограничения на класс алгоритмов адаптации. Формально эти ограничения сводятся к требованию рекуррентности алгоритма адаптации (3.15), когда формирование новых оценок параметров τ_k+1 производится по старым оценкам τ_k с учетом только текущей информации (без запоминания всей предыстории самонастройки). Поэтому естественно искать решение эстиматорных неравенств (3.13) в классе рекуррентных алгоритмов градиентного типа

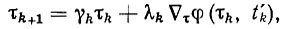(3.41)

где γ_k, λ_k - параметры алгоритма адаптации; Δ_τφ( τ_k, t'_k) - градиент функции φ( τ, t) по τ в точке τ= τ_k, t = t'_k.

Логика коррекций параметров закона управления (3.27) в соответствии с рекуррентным алгоритмом адаптации (3.15) и (3.41) очень проста: оценка τ,sub>k на k-м интервале управления не изменяется, если эстиматорные неравенства выполняются, в противном случае осуществляется адаптивная коррекция в первый момент нарушения неравенств t'_k при t> t_k. Для коррекции нужна только информация о значении эстиматорной φ функции в момент t'_k т. е. информация о факте и о степени нарушения неравенств (3.13). Такая рекуррентная схема не требует памяти для хранения информации о нарушении эстиматорных неравенств в предыдущие моменты времени.

Существенное влияние на быстроту сходимости и другие свойства рекуррентных алгоритмов адаптации (3.41) оказывает выбор параметров γ_k, λ_k. Естественно подчинить этот выбор требованию конечности времени адаптации.

Критерий конечности времени адаптации можно записать в виде

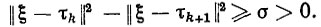(3.42)

Смысл этого критерия заключается в следующем: на каждом шаге алгоритма расстояние от текущей оценки τ_k до неизвестного вектора параметров ξ убывает на конечную величину. Вследствие этого число коррекций r конечно и удовлетворяет оценке

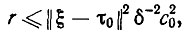(3.43)

где с₀=sup ||Δ_τφ(τ_k,t'_k)||- Подставляя эту оценку в соотношение (3.40), получим оценку сверху для времени адаптации. Рассмотрим класс рекуррентных алгоритмов адаптации вида (3.41)с параметрами

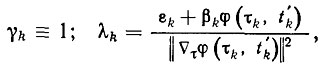(3.44)

выбираемыми из условия (3.42). Если 0≤ε_k≤2δ, 0≤β_k≤2, то алгоритм (3.41), (3.44) удовлетворяет критерию конечности времени адаптации (3.42). При специальном выборе параметров и β_k этот алгоритм приводит к некоторым алгоритмам адаптации, ранее полученным в работах [132, 142].