3.7. Оптимизация и акселеризация алгоритмов адаптации

Одной из важнейших проблем при синтезе алгоритмов адаптации является их оптимизация. Применительно к дискретным алгоритмам адаптации это означает, что оператор адаптации А в (3.15) на каждом шаге алгоритма должен выбираться исходя из условия минимизации заданного функционала качества адаптации.

Значительный практический интерес представляют локальные функционалы вида (3.24) и интегральные функционалы вида (3.22) или (3.25). Функционал (3.24) характеризует расстояние от оценки τ_k до неизвестного вектора параметров ξ, поэтому будем называть его идентификационным.

Весьма заманчиво синтезировать оператор адаптации из условия минимизации функционала качества (3.24). Однако до последнего времени считалось, что такой критерий оптимальности нельзя использовать для синтеза алгоритма адаптации, так как вектор ξ, входящий в (3.24), неизвестен и, следовательно, искомый оператор адаптации будет зависеть от неизвестных величин. В связи с этим казалось очевидным, что соответствующие оптимальные алгоритмы адаптации не реализуемы и поэтому не могут найти применения в адаптивных системах управления. Однако более глубокий анализ показывает, что высказанные соображения справедливы лишь отчасти и в ряде случаев не являются препятствием для синтеза и непосредственного использования оптимальных алгоритмов адаптации. Этот факт был установлен в работах [107, 109]. Там же предложен описываемый ниже метод синтеза локально оптимальных дискретных алгоритмов адаптации и установлены условия их реализуемости. Приведем здесь некоторые оптимальные алгоритмы, представляющие наибольший интерес для адаптивного программного управления РТК.

Синтезируем оптимальный рекуррентный алгоритм адаптации вида (3.41) из условия минимизации идентификационного функционала (3.24). Рассмотрим важный частный случай, когда γ_k=1. В этом случае оптимальные параметры λ_k определяются по формуле

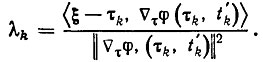(3.45)

Отметим, что здесь (как, впрочем, и в других рассматриваемых ниже оптимальных алгоритмах адаптации) оптимальные параметры зависят от неизвестного вектора ξ. Однако в рассматриваемой схеме адаптивного программного управления эта зависимость такова, что известно скалярное произведение τ φ( τ,t). Так, например, для эстиматорных неравенств вида (3.28) оно равно величине (u, u-U (х, ẋ, τ)) >|| u-U (х, ẋ1, τ)||^-1. Отсюда следует, что оптимальные параметры (3.45) на самом деле выражаются через известные на каждом шаге величины.

Таким образом, синтезированный локально оптимальный алгоритм адаптации реализуем. Нетрудно показать, что число коррекций этого алгоритма удовлетворяет верхней оценке (3.43) и, следовательно, время адаптации конечно.

Рассмотренный градиентный алгоритм адаптации имеет простую геометрическую интерпретацию. Эстиматорные неравенства (3.13) определяют в пространстве настраиваемых параметров выпуклые области, которые имеют общую точку ξ (и даже общий шар, радиус которого тем больше, чем больше величина δ). Оценка τ_k не изменяется, если неравенства (3.13) выполнены при τ= τ_k т. е. τ_k находится внутри соответствующей выпуклой области. При нарушении неравенств в момент t"_k к вектору τ_k прибавляется вектор Δτ φ( τ_k, t'_k), направленный внутрь области, причем величина шага определяется формулой (3.45) и такова, что φ( τ_k+1, t'_k)=δ.

Совершенно аналогично определяются оптимальные параметры γ_k и λ_k в общем случае рекуррентных градиентных алгоритмов вида (3.41). Явные формулы этих алгоритмов и их свойства рассмотрены в работах [107, 109].

Значительный интерес представляет также оптимизация рекуррентных алгоритмов адаптации по отношению к эстиматорному функционалу качества. Примером такого функционала может служить функционал

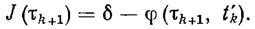(3.46)

Рассмотрим рекуррентный алгоритм адаптации (3.41), где γ_k=1, а параметр λ_k выбирается на каждом шаге из условия минимизации функционала (3.46), т. е.

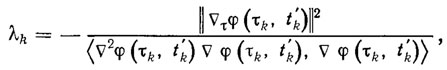(3.47)

где Δ² φ (τ, t) - матрица вторых производных функции φ по τ.

Отметим, что описанный метод синтеза алгоритма адаптации аналогичен методу наискорейшего спуска в задачах оптимизации.

На практике быстрота сходимости описанных рекуррентных алгоритмов адаптации может оказаться недостаточной, поэтому возникает необходимость в акселеризации алгоритмов, направленной на сокращение общего времени адаптации.

Простейший способ акселеризации рекуррентных алгоритмов (3.41) с γ_k=1 заключается в замене скалярного параметра λ_k матричным параметром Λ_k и в определении последнего из условия оптимизации, например эстиматорного функционала (3.46). Если матрицы Δ²_τ(τ_k,t'_k) не вырождены, то получаем

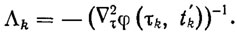(3.48)

Для эстиматорных неравенств вида (3.26) или (3.28) τ_k+1=ξ. Это означает, что синтезированный оптимальный алгоритм обеспечивает точную идентификацию ξ за один шаг, и, следовательно, время адаптации μ<0. Отметим, что этот алгоритм с оптимальным параметром (3.48) аналогичен методу Ньютона.

Преимущество акселерантного оптимального алгоритма адаптации (3.41), (3.48) перед другими рекуррентными алгоритмами заключается в высокой быстроте сходимости и точности адаптации. Однако трудность вычислений на одном шаге этого алгоритма определяется необходимостью обращения матрицы вторых производных ⏊ τ φ(τ0, t'_k) (при условии, что она не вырождена) и может оказаться чрезмерно высокой. В то же время локально оптимальные алгоритмы адаптации вида (3.41), (3.45) или (3.47), не требующие вычисления и обращения матрицы Δ2τφ( τ,t), существенно проще для вычисления. При этом они обеспечивают решение эстиматорных неравенств (4.1) через конечное число шагов.

Таким образом, вопрос о целесообразности применения акселерантных или обычных рекуррентных алгоритмов адаптации тесно связан с проблемой эффективности всего процесса в целом, т. е. с общим объемом вычислений, затрачиваемых на адаптацию. В связи с этим возникает задача конструирования акселерантных алгоритмов адаптации, менее трудоемких, чем оптимальный алгоритм (3.41), (3.48), но обладающих существенно большей быстротой сходимости по сравнению с обычными рекуррентными алгоритмами вида (3.41), (3.44) или (3.45).

Рассмотрим решение задачи акселеризации в классе много шаговых алгоритмов адаптации, параметры которых также выбираются из соображений локальной оптимизации. Особый интерес представляет много шаговый градиентный алгоритм с полной памятью вида

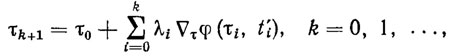(3.49)

где τ₀ - произвольная начальная оценка; λ_i - шаг адаптации в направлении Δτφ(τi, t'_i).

Существенное влияние на свойства алгоритма адаптации (3.49) оказывает выбор параметров λ_i = 0, 1, ...,k. Будем искать эти параметры из условия минимизации идентификационного функционала качества (3.24). Обозначим через Λ_k вектор, компонентами которого являются искомые параметры λ0,λ1, ..., λ_k. Тогда оптимальные параметры определяются формулой [107, 109]

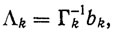(3.50)

где 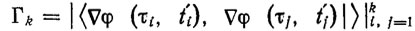- матрица Грама, a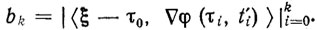

Как показано в работе [1091, число коррекций оптимального алгоритма (3.49), (3.50) не превышает размерности пространства настраиваемых параметров, т. е. k≤ р. Следовательно, для времени адаптации справедлива оценка μ≤pθ.. Акселерантный оптимальный алгоритм (3.49), (3.50) обеспечивает на последнем шаге точную идентификацию вектора неизвестных параметров ξ.