3.8. Методы и режимы адаптивного программного управления

Основываясь на изложенной выше концепции алгоритмического конструирования адаптивных систем программного управления, перейдем теперь к описанию конкретных методов адаптивного управления в характерных для РТК режимах стабилизации ПД, терминального управления и самонаведения. Эти методы отличаются в основном типом эстиматорных неравенств, что предопределяет явный вид алгоритмов адаптации и свойства переходных процессов.

Общим для всех методов и режимов является использование законов управления (регуляторов) вида (3.27), где Г - устойчивая n*n-матрица коэффициентов усиления, выбираемая из условия обеспечения желаемого характера переходных процессов, а τ - текущая оценка неизвестного вектора ξ, вычисляемая в силу некоторого алгоритма адаптации. В качестве алгоритма адаптации можно взять любой реализуемый алгоритм вида (3.14) или (3.15), дающий решение эстиматорных неравенств (3.13). Заметим, что в процессе самонастройки распределение моментов времени нарушения эстиматорных неравенств заранее неизвестно; заранее неизвестны и величины коррекции оценок τ: они определятся в ходе управления РТК на основе сигналов обратной связи. Целью управления РТК в режиме стабилизации РД является отслеживание ПД с заданной точностью в соответствии с условием (3.16) при соблюдении конструктивных ограничений на состояния и управления. Ради простоты изложения будем считать, что неизвестный параметр ξ фиксирован, а внешние возмущения π отсутствуют. Распространение предлагаемых методов на более широкие классы неопределенности типа (3.4) и (3.5) обычно затруднений не вызывает.

Первый метод адаптивной стабилизации ПД основывается на конструировании и решении эстиматорных неравенств вида (3.28). Он особенно удобен в тех случаях, когда оператор управления U линеен по третьему аргументу, т. е. имеет место представление (3.29). Синтезируем искомый закон адаптивной стабилизации в виде (3.27) и изучим его свойства. Прежде всего заметим, что ввиду разрешимости (с запасом δ) и выпуклости неравенств (3.28) для их решения можно использовать описанные выше алгоритмы с конечным временем адаптации. Рассмотрим для определенности дискретные алгоритмы адаптации вида (3.15). В этом случае время адаптации μ не превышает величины r₀.

Характер переходных процессов в РТК при адаптивном программном управлении (3.27) и (3.15) определяется уравнением (3.18). В рассматриваемом случае справедлива оценка [107, 111]

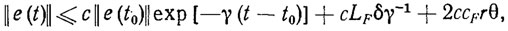
где L_F и C_F - параметры, зависящие от вида функции F в уравнении динамики РТК (3.1). Из данной оценки следует, что достижимая точность стабилизации (отслеживания) ПД определяется соотношением

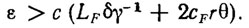(3.51)

Очевидно, что путем специального выбора матрицы коэффициентов усиления Г регулятора (с достаточно большим запасом устойчивости γ), увеличения точности эстиматора и быстродействия адаптатора (что соответствует выбору достаточно малых параметров δ и θ) можно обеспечить любую наперед заданную точность отслеживания ПД. При этом время переходного процесса оценивается соотношением

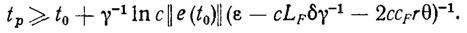(3.52)

Из этого соотношения следует, что если ПД х_p (t) рассчитано исходя из состояния РТК в начальный момент времени, т. е. e(t₀)=0, то время переходного процесса обращается в нуль. Это означает, что целевое условие (3.16), требующее е-близости реального и программного движений РТК, будет выполнено с самого начала. Такой результат при наличии производственных возмущений и не определенностей достигается за счет адаптивной настройки (самонастройки) параметров закона управления (3.27) с помощью конечных алгоритмов адаптации вида (3.15).

Второй метод адаптивного управления в режиме отслеживания заданного ПД основывается на конструировании и решении эстиматорных неравенств вида (3.26). Этот метод рекомендуется применять в тех случаях, когда динамическая модель РТК обладает свойством (3.21). В этих случаях эстиматорные неравенства (3.26) выпуклы и для их решения вновь применимы конечные алгоритмы адаптации вида (3.14), (3.15), в частности оптимальный акселерантный алгоритм (3.49), у которого время адаптации μ≤pθ. Использование этого алгоритма в законе программного управления (3.27) обеспечивает (при отсутствии внешних возмущений π) точную идентификацию вектора неизвестных параметров ξ и, как следствие, желаемый характер переходных процессов. Время переходного процесса оценивается соотношением (3.52).

Рассмотренные методы адаптивного отслеживания ПД требуют организации обратных связей не только по вектору состояний но и по его производной х. Однако прецизионное измерение (или точное оценивание) ẋ на практике зачастую наталкивается на значительные трудности. Этим определяется необходимость разработки такого метода адаптивного программного управления РТК, при реализации которого нужна обратная связь только по вектору состояний х.

Основу третьего метода составляют эстиматорные неравенства интегрального типа, построенные в п. 3.4. Для решения этих неравенств непосредственно применимы алгоритмы адаптации, синтезированные в п. 3.5-3.7. Использование этих алгоритмов в сочетании с законом управления (3.27) позволяет отследить ПД с точностью ε, определяемой из условия [107]

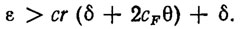(3.53)

При реализации данного метода нужны датчики сигналов обратной связи только по вектору состояний РТК.

Как видно из расчетных соотношений (3.51) и (3.53), точность осуществления ПД для трех рассмотренных методов лимитируется точностью δ решения эстиматорных неравенств. При этом адаптационные возможности регулятора (3.27) тем выше, чем больше быстродействие адаптатора, т. е. чем меньше время адаптивной коррекции 0 и общее время адаптации μ. Важно отметить, что при отсутствии начальных возмущений, т. е. при е (t₀)=0, все три метода обеспечивают осуществление ПД с заданной точностью с самого начала, т. е. время переходного процесса равно нулю.

Резюмируя вышеизложенное, можно утверждать: если регулятор имеет достаточно большой запас устойчивости (т. е. параметр ν достаточно велик), точность эстиматора и быстродействие адаптатора достаточно велики (т. е. достаточно малы параметры δ и θ), то синтезированные законы адаптивной стабилизации ПД обеспечивают достижение цели управления (3.16) с любой наперед заданной точностью е при соблюдении конструктивных ограничений (3.2) и (3.3) в заданном классе неопределенности (3.4), (3.5).

Рассмотрим теперь особенности адаптивного управления РТК в режимах терминального управления и самонаведения. Цели адаптивного терминального управления и самонаведения заключаются в выполнении целевого неравенства (3.17) при соблюдении конструктивных ограничений на состояния и управления (3.2) и (3.3) в заданном классе неопределенности {Q_ξ,Q_π} Основная идея решения задачи терминального управления состоит в том, чтобы исходя из заданных граничных условий на начальное и конечное состояния РТК и конструктивных ограничений (3.2),(3.3) предварительно рассчитать ПД, а затем стабилизировать это ПД с помощью одного из синтезированных выше законов адаптивного программного управления.

Адаптивная система управления РТК в режиме терминального управления работает следующим образом. Сначала программатор рассчитывает ПД х_p(t), t∈[t₀,t_τ]. При этом вычислительный процесс построения и оптимизации ПД может быть организован с помощью методов и алгоритмов, предложенных в гл. 3. После этого регулятор (автомат стабилизации), используя сигналы обратной связи, формируемые информационной системой, синтезирует закон управления ПД вида (3.27).

Самонастройка параметров регулятора осуществляется адаптатором, реализующим некоторый алгоритм адаптации вида (3.14) или (3.15). Структура и режим работы адаптатора определяются эстиматором, реализующим эстиматорные неравенства вида (3.26) или (3.28). Алгоритм адаптации синтезируется как алгоритм решения этих неравенств, причем время адаптации μ не должно превышать времени движения Т=t,sub>T-t₀.

Специфика адаптивного терминального управления заключается в отсутствии начальных возмущений. Это связано с тем, что в режиме терминального управления ПД рассчитывается исходя из того начального состояния, в котором фактически находится РТК, т. е. х_p (t₀)=x(t₀). Сформулируем условия, гарантирующие решение задачи адаптивного терминального управления в заданном классе неопределенности Q_ξ. Закон управления определим формулой (3.27). Если оператор управления U представим в виде (3.29), то естественно воспользоваться первым методом адаптивной стабилизации ПД, основанным на решении эстиматорных неравенств вида (3.28). В этом случае справедлива следующая оценка качества переходных процессов:

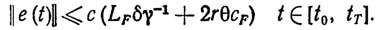(3.54)

Эта оценка непосредственно вытекает из (3.50). Как видно из (3.54), предельная точность адаптивного терминального управления определяется соотношением (3.51). В тех случаях, когда функция F в уравнении динамики РТК (3.1) представима в виде (3.21), целесообразно воспользоваться либо вторым методом адаптивного управления (если измеряются как вектор состояний РТК х, так и его производная ẋ), либо третьим методом (если измеряется только вектор состоянийх). При этом ПД х_p и его производная ẋ_p должны строиться внутри заданных множеств Q_x и Qẋ с некоторыми "запасами". Тогда автоматически будут выполняться конструктивные ограничения на состояния и управления, определяемые соотношениями (3.2) и (3.3). Следовательно, цель терминального управления (3.17) РТК будет достигнута с учетом имеющихся ограничений на состояния и управления (3.2) и (3.3).

Таким образом, точность терминального управления, т. е. точность перевода РТК в заданное динамическое состояние х₁ лимитируется прежде всего такими параметрами, как точность δ эстиматора и быстродействие θ адаптатора. Расчет управления в рассматриваемом режиме как раз и сводится к выбору приемлемых значений этих параметров, а также параметров с и γ, зависящих от выбора матрицы коэффициентов усиления Г регулятора, и параметра r, характеризующего предельное число коррекций дискретного алгоритма адаптации.

Для увеличения точности достижения цели можно воспользоваться следующим приемом: в ходе управления нужно осуществлять не только коррекцию параметров закона управления (3.27), но и коррекцию самого ПД. При коррекции ПД следует всякий раз исходить из того реального состояния, в котором РТК оказался в момент коррекции. В качестве моментов коррекции ПД целесообразно выбирать моменты коррекции параметров закона управления (3.27). Тогда процессы пересчета ПД и адаптации будут протекать параллельно, обеспечивая высокую точность и надежность работы РТК.

Совершенно аналогично синтезируется адаптивное управление РТК в режиме самонаведения. Главное его отличие от режима терминального управления заключается в том, что при самонаведении указывается только требуемое динамическое состояние РТК х₁ а ПД вообще не строится. При этом время самонаведения заранее не фиксируется.

Для синтеза структуры и расчета параметров системы адаптивного управления в режиме самонаведения можно использовать описанные выше три метода адаптивной стабилизации ПД. Однако они должны быть модифицированы. Эта модификация заключается в том, что в закон управления (3.27) вместо ПД х_p следует подставить заданное целевое состояние РТК х₁ тогда закон адаптивного самонаведения примет вид

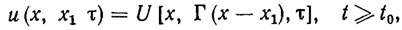(3.55)

где Г - устойчивая п*n-матрица коэффициентов усиления в каналах обратной связи; τ - вектор настраиваемых параметров, формируемый тем или иным алгоритмом адаптации.

Таким образом, описанная методология конструирования и расчета адаптивных систем управления РТК в режимах терминального управления и самонаведения гарантирует выполнение целевых условий и конструктивных ограничений на состояния и управления в заданном классе неопределенности условий эксплуатации РТК. При этом качество адаптивного терминального управления и самонаведения тем выше, чем больше запас устойчивости регулятора, точность эстиматора и быстродействие адаптатора.