Глава 5. Манипуляционные роботы с адаптивным управлением

5.1. Сравнительный анализ систем программного и адаптивного управления

Современные методы проектирования систем программного управления роботов основываются на более или менее точной информации о конструктивных особенностях манипуляционного механизма и условиях эксплуатации робота. При этом система управления обычно рассчитывается исходя из упрощенной модели динамики для некоторых фиксированных (номинальных) производственных условий. Однако на практике эти условия могут непредсказуемо меняться и сильно отклоняться от номинальных, а упрощение модели динамики робота снижает качество синтезируемого управления. Вследствие этого системы программного управления зачастую не обеспечивают выполнение заданных технологических операций с требуемой точностью и быстродействием во всем диапазоне неконтролируемых изменений производственной обстановки.

Одной из главных причин резкого ухудшения качества традиционных систем числового программного управления (вплоть до полной потери работоспособности) являются разного рода внешние возмущения и непредсказуемый дрейф параметров, существенно влияющие на динамику робота и, в частности, на точность выполнения технологических операций. Поэтому представляется целесообразным прежде всего оценить влияние указанных возмущений на качество программного управления. С этой целью рассмотрим динамическую модель манипулятора, описываемую векторным дифференциальным уравнением Лагранжа вида:

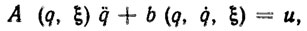(5.1)

где q - m-мерный вектор обобщенных координат манипулятора; 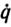, 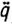- первая и вторая производные q по времени t; ξ - p - мерный вектор параметров манипулятора и груза; u - m-мерный вектор управляющих моментов, вырабатываемых системой исполнительных приводов; А (q, ξ), b (q, 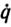, ξ) - заданные m*m- матрица-функция и m-вектор-функция, определяемые особенностями конструкции манипулятора.

Наиболее чувствительным к действию внешних и параметрических возмущений являются системы контурного управления. Поэтому проанализируем влияние этих факторов на качество переходных процессов при отслеживании роботом заданной программной траектории q_p(t). Задача контурного управления заключается в синтезе стабилизирующего закона управления, обеспечивающего осуществление программной траектории с заданной точностью. Решение этой задачи существенно осложняется наличием начальных и неизвестных параметрических возмущений. Мерой начальных возмущений является величина

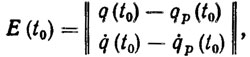
а мерой параметрических возмущений - величина

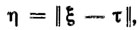
где τ - оценка параметров ξ уравнения движения (5-1), используемая в стабилизирующем законе управления.

Если бы начальных и параметрических возмущений не было, т. е. Е (t₀)=0 и ξ = τ, то программное управление вида

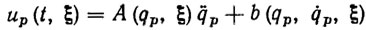(5.2)

обеспечило бы точное отслеживание заданной программной траектории. Однако на практике почти всегда имеются начальные и параметрические возмущения. Поэтому, строго говоря, воспользоваться управлением (5.2) нельзя. Если все же им воспользоваться, подставив вместо неизвестного вектора ξ некоторую его оценку τ, то неизбежно возникнут автоколебания или даже потеря устойчивости. Вследствие этого программная траектория q_p(t) не будет отслежена, а робот может оказаться в аварийном состоянии. Таким образом, приходится констатировать, что программное управление (5.2) неэффективно, а в ряде случаев практически не-приемлемо. Возникает необходимость в синтезе законов управления по принципу обратной связи. Простейший закон такого типа легко синтезируется на основании формулы (5.2) и имеет вид [107, 112]

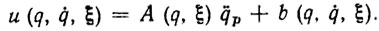(5.3)

Этот закон обеспечивает устойчивость программной траектории q_p(t) по отношению к начальным возмущениям. Для его реализации нужно точно знать параметры ξ и организовать обратные связи по всем компонентам векторов q и 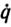. Однако для надежного отслеживания программной траектории с заданной точностью этого недостаточно. Важно, чтобы закон управления роботом обладал достаточно сильным стабилизирующим эффектом, т. е. обеспечивал асимптотическую устойчивость q_p(t). В этом случае при любом уровне начальных возмущений динамическая ошибка e=q- q_p(t) будет стремиться к нулю.

Искомый стабилизирующий закон программного управления имеет вид [107, 112]

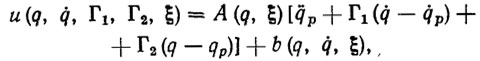(5.4)

где Γ₁, Γ₂ - такие матричные коэффициенты усиления в каналах обратной связи, что корни уравнения det||Iλ²+Γ₁λ+ Γ₂||=0 (где I - единичная матрица) имеют отрицательные действительные части. В этом случае динамическая ошибка удовлетворяет линейному дифференциальному уравнению вида

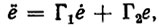(5.5)

откуда непосредственно следует, что ошибка асимптотически затухает. Этот факт как раз и означает, что программная траектория асимптотически устойчива. Более того, выбором Γ₁ и Γ₂ конструктор системы управления может обеспечить желаемый (например, экспоненциальный) характер затухания динамической ошибки и полностью исключить взаимное влияние каналов управления, т. е нейтрализовать перекрестные связи. Для этого достаточно взять в качестве Γ₁ и Γ₂ диагональные матрицы вида [112]

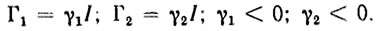(5.6)

Другой (классический) способ синтеза стабилизирующего управления заключается в использовании программного управления в сочетании с линейной обратной связью по ошибке e и скорости ее изменения ė . Соответствующий стабилизирующий закон управления с линейной обратной связью имеет вид

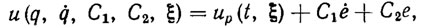(5.7)

где C₁ и С₂ -матричные коэффициенты усиления в каналах обратной связи" выбираемые из условия асимптотической устойчивости программной траектории в замкнутой системе (5.1), (5.7).

Недостатком контурного управления (5.7) по сравнению с (5.3) является сложность априорного выбора коэффициентов усиления С₁ и С₂, вследствие чего эти коэффициенты обычно подбираются экспериментально в процессе ручной настройки системы управления робота. Только в отдельных случаях [например, если уравнение динамики робота (5.1) линейно] существует регулярная процедура обоснованного выбора коэффициентов усиления С₁ и С2 в зависимости от параметров ξ робота.

В манипуляционных роботах промышленного назначения широко используются различные схемы локального сервоуправления, в основе которых лежит идея линейного пропорционально-дифференциально-интегрального (ПИД) регулирования. В обобщенном виде эти схемы описываются формулой вида

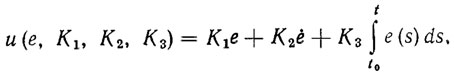(5.8)

где K₁, К₂, К₃ - экспериментально подбираемые матричные коэффициенты усиления. При K₂=K₃=0 получаем пропорциональный регулятор, а при К₁=К₃=0 и К₁=K₂=0 - соответственно дифференциальный и интегральный регуляторы.

Достоинством ПИД-регуляторов является чрезвычайная простота их реализации, не требующая никакой информации о параметрах ξ робота. Однако им присущ и целый ряд недостатков. Во-первых, они требуют ручной настройки параметров К₁, К₂, К₃ и зачастую теряют работоспособность при резком изменении параметров ξ (например, при изменении массы груза). Во-вторых, они не обладают требуемым стабилизирующим эффектом, вследствие чего динамическая ошибка имеет незатухающий колебательный характер и заданная точность контурного управления зачастую не достигается. В-третьих, при управлении по формуле (5.8) полностью игнорируются перекрестные связи в каналах управления, порожденные взаимным влиянием звеньев манипулятора и груза. Это существенно ухудшает качество контурного управления.

Проанализируем качество переходных процессов при отслеживании заданной программной траектории с помощью наиболее совершенного стабилизирующего закона управления вида (5.4), (5.6). При реализации этого закона приходится вместо неизвестных параметров ξ робота и груза (которые к тому же могут не предсказуемо дрейфовать в широких пределах) использовать их оценки τ. Это приводит к неконтролируемым параметрическим возмущениям, которые в сочетании с начальными возмущениями неблагоприятно влияют на точность контурного управления.

Аналитическое исследование степени этого влияния для различных законов контурного управления [включая и законы управления (5.2), (5.3), (5.7), (5.8)] приведено в монографии [42]. Результатом этих исследований являются следующие основные выводы:

1. благодаря стабилизирующему эффекту влияние начальных возмущений на качество контурного управления, описываемого соотношениями (5.4), (5.6), становится с течением времени исчезающе малым;
2. неконтролируемые параметрические возмущения могут приводить к автоколебаниям и неустойчивости программной траектории [особенно этот вывод касается законов управления (5.2)и (5.8)];
3. предельно достижимая точность контурного управления зависит от уровня параметрических возмущений: чем выше этот уровень, тем ниже точность отслеживания данной программной траектории.

Эффективным средством обеспечения заданного качества управления и парирования неконтролируемых параметрических возмущений является адаптивный подход. Согласно этому подходу стабилизирующий закон управления типа (5.4), (5.6) должен быть дополнен алгоритмом адаптивной настройки (самонастройки) параметров.

Адаптация системы управления робота реализуется в много шаговом процессе принятия решений путем самонастройки параметров стабилизирующего закона программного управления с учетом управляющих и возмущающих воздействий. Тем самым управляющие воздействия используются не только для осуществления желаемой траектории движения, но и для более точного определения характеристик робота и конкретных условий его функционирования.

Адаптивные системы управления роботов, конечно, сложнее, чем традиционные системы программного управления. Однако при наличии достаточно мощных управляющих ЭВМ и микропроцессоров такое усложнение в разумных пределах вполне допустимо. В то же время открывается возможность построения принципиально новых адаптивных роботов, обладающих высокоразвитой способностью самонастраиваться и автоматически приспосабливаться к заранее неизвестным и изменяющимся условиям эксплуатации.

Эта способность точно и надежно выполнять требуемые технологические операции в не детерминированной рабочей обстановке обеспечивается использованием дополнительных датчиков (или, как принято говорить, очувствлением робота) и введением в систему программного управления элементов (алгоритмов) адаптации. Такое расширение информационных и адаптационных возможностей при переходе от программных роботов к адаптивным, как правило, не влечет за собой коренных изменений в конструкции робота и структуре его системы управления. Дело сводится просто к организации дополнительных обратных связей через соответствующие датчики внутренней и внешней информации и к программной реализации новых программных модулей (эстиматор, адаптатор и т. п.), реализующих процесс адаптации. В этом проявляется преемственность при проектировании более совершенных систем адаптивного управления на базе обычных систем программного управления.

В простейшем случае параметрической адаптации стабилизирующие законы управления приводами манипулятора дополняются алгоритмами самонастройки, обеспечивающими автоматическое приспособление системы управления к изменению параметров (например, к изменению массо-инерционных характеристик груза). Для придания роботу способности к параметрической адаптации достаточно заменить его сервоприводы на самонастраивающиеся приводы. Отличительной чертой последних является нечувствительность (инвариантность) по отношению к параметрическим возмущениям.

Таким образом, при параметрической адаптации подлежат изменению в основном только регуляторы системы приводов (например, вместо обычных ПИД-регуляторов используются адаптивные ПИД-регуляторы). При этом зачастую не возникает необходимости в дополнительном "очувствлении" робота.

Непараметрическая адаптация систем управления роботов более сложна и многообразна. К ней относятся изменения структуры регуляторов в зависимости от сложившейся ситуации, коррекция программных траекторий (например, при манипулировании неориентированными деталями или при появлении препятствий) и т. п.

Программа поведения робота в не детерминированной среде принципиально не может быть задана заранее. Она формируется в процессе функционирования робота с учетом фактической обстановки. При этом возникает потребность в распознавании ситуаций, анализе рабочей обстановки, планировании действий и т. д. В подобных случаях адаптивная система управления роботом снабжается соответствующими элементами искусственного интеллекта.