5.2. Алгоритмический синтез адаптивных систем контурного и позиционного управления

Рассмотрим особенности синтеза адаптивных систем контурного управления манипуляционными роботами, обеспечивающими отслеживание манипулятором заданной программной траектории

q_p(t) с требуемой точностью. Будем считать, что конкретные значения параметров ξ робота и груза неизвестны, а известно лишь множество Q_ξ. их возможных значений. На практике параметры ξ могут непредсказуемо изменяться в процессе функционирования робота. Например, могут изменяться масса и моменты инерции груза, коэффициенты трения в исполнительных приводах и т. п.

Благодаря адаптации к неопределенности и дрейфу параметров искомый алгоритм управления с обратной связью должен обеспечить требуемую близость реальной и программной траекторий для любых возможных значений параметров ξ из множества Q_ξ т. е. должно выполняться целевое условие

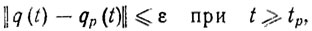(5.9)

где ε - положительное число, определяющее требуемую точность отслеживания программной траектории q_p (t); t_p≥t₀ - наименьший момент времени, начиная с которого выполняется целевое неравенство (5,9); t_p-t₀ - время переходного процесса адаптации.

При расчете и проектировании адаптивных систем контурного управления важно иметь возможность выбирать параметры системы управления таким образом, чтобы время переходного процесса было, по возможности, равным нулю. Тогда цель контурного управления - отслеживание заданной программной траектории с точностью ε - будет выполнена с самого начала.

Для решения сформулированной задачи воспользуемся методом адаптивного программного управления, изложенным в гл. 3. Согласно этому методу задача решается в три этапа. Сначала строится стабилизирующий закон управления, обеспечивающий асимптотическую устойчивость программной траектории в предположении, что параметры ξ робота и груза известны. Затем на основе этого не адаптивного закона управления конструируются вспомогательные эстиматорные неравенства относительно параметров закона управления, из выполнения которых непосредственно следует выполнение целевых неравенств (5.9). На третьем этапе синтезируются алгоритмы решения этих вспомогательных неравенств, трактуемые как алгоритмы адаптивной настройки (самонастройки) параметров системы управления. При этом важно, чтобы алгоритмы самонастройки обладали свойством конечной сходимости. Кроме того, желательно, чтобы они были оптимальными в смысле некоторого разумно выбранного и строго сформулированного критерия качества адаптации. Поэтому в дальнейшем изложении особое внимание будет уделено синтезу оптимальных алгоритмов адаптации, обладающих достаточно высокой скоростью сходимости.

Переходя к рассмотрению первого этапа построения адаптивного управления, предположим временно, что параметры ξ уравнения динамики (5.1) известны. В этом случае можно воспользоваться стабилизирующим законом управления (5.4), (5.6), синтезированным исходя из требования обеспечения желаемого (например, экспоненциального) характера переходного процесса. Заметим, что левая часть уравнения динамики робота (5.1) представлена в виде

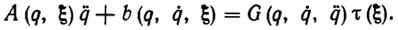(5.10)

Используя свойство (5.10), представим стабилизирующее программное управление в виде

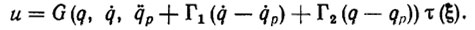(5.11)

Однако непосредственно реализовать это управление нельзя, так как параметры ξ неизвестны.

Идея адаптивного контурного управления заключается в замене неизвестных параметров ξ их оценками τ, алгоритм определения которых строится таким образом, чтобы было выполнено целевое условие (5.9). Итак, определим адаптивное контурное управление в виде:

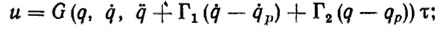(5.12)

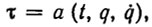(5.13)

где a - оператор адаптации, который нужно построить исходя из формулируемых ниже требований.

Рассмотрим вспомогательные эстиматорные неравенства вида

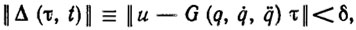(5.14)

где δ>0 - параметр, определяющий точность эстиматора. Очевидно, что неравенства (5.14) разрешимы при τ=ξ с "запасом" δ. Заметим еще, что эти неравенства выпуклы по τ. Эти свойства эстиматорных неравенств (5.14) позволяют применить для их решения рекуррентные или много шаговые оптимальные алгоритмы адаптации, описанные в гл. 3.

Все такие алгоритмы имеют следующий вид:

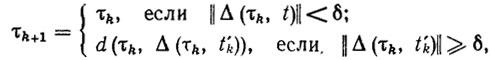(5.15)

где t'_k - первый момент времени из интервала (t_k, t_k+1], при котором нарушаются неравенства (5.14); τ₀t₀) - произвольный p-мерный вектор начального приближения из множества Q_ξ. Важно отметить, что из выполнения эстиматорных неравенств (5.14) следует выполнение целевых неравенств (5.9) с некоторым ε= ε(δ).

Используя методику оценки динамической ошибки, описанную в третьей главе, легко получить следующее соотношение:

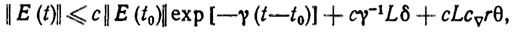(5.16)

где с и γ - положительные числа, зависящие от выбора только матриц коэффициентов усиления Γ₁ и Γ₂ в (5.12); L и c_Δl - константы, определяемые особенностями двигательной системы ро-бота.

Предположим, что начальных возмущений нет, т. е. Е(t₀)=0. Этого можно достичь, если задавать программную траекторию q_p(t) исходя из того начального состояния, в котором робот находится в момент времени t₀. Тогда достижимая точность контурного управления определяется соотношением

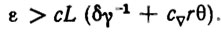(5.17)

Неравенство (5.17) представляет собой расчетное соотношение для обоснованного выбора параметров адаптивной системы контурного управления. Варьируя параметры регулятора (числа с и γ), эстиматора (число δ) и адаптатора (числа r и θ), конструктор может обеспечить любую наперед заданную точность е отслеживания программной траектории. Из соотношения (5.17) видно, что эта точность тем выше, чем больше (при прочих равных условиях) быстродействие адаптатора и точность эстиматора.

Таким образом, синтезированы алгоритмы и получены расчетные соотношения, позволяющие конструктору адаптивной системы контурного управления обоснованно выбирать параметры регулятора, эстиматора и адаптатора исходя из требования отслеживания манипулятором программной траектории с любой наперед заданной точностью.

Широкий класс технологических операций, возлагаемых на роботов, сводится к переводу манипулятора из некоторой фиксированной конфигурации q₀, рассматриваемой как начальная, в желаемую конечную, при которой рабочий орган оказывается в требуемой позиции. Основным требованием к качеству управления в этой задаче является точное позиционирование рабочего органа. Иногда дополнительно задается время выполнения операции, диктуемое темпом технологического процесса. Подобные ситуации возникают, например, при обслуживании роботом станков с ЧПУ, конвейеров и т. п.

Перейдем к более точной формализованной постановке задачи адаптивного позиционного управления. Пусть заданы начальная и конечная конфигурация манипулятора q(t₀)=q₀ и q(t_x)=q₁ и время перевода T=t_T-t₀. Параметры ξ робота и груза неизвестны могут изменяться в пределах заданного множества Q_ξ, характеризующего априорную неопределенность условий функционирования робота.

Требуется синтезировать адаптивный закон управления и (q, 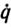, τ), переводящий манипулятор из состояния q₀ в состояние q₁ за время Т с заданной точностью ε, т. е.

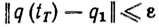(5.18)

для любых неизвестных значений параметров ξ из заданного множества Q_ξ. Решение этой задачи (по аналогии с решением задачи контурного управления) будем искать поэтапно. На первом этапе синтезируем искомый закон позиционного управления в предположении, что параметры ξ уравнения динамики (5.1) известны.

Программная траектория, переводящая манипулятор из заданного начального состояния q₀, 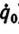в желаемое конечное состояние q₁ 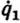определяется формулой

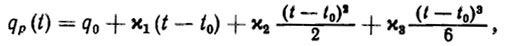(5.19)

где

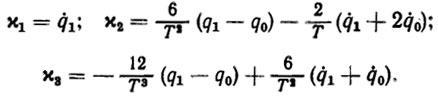
Идеальный (не адаптивный) закон позиционного управления, нацеливающий на достижение конечного состояния в момент времени t_T имеет вид

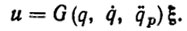(5.20)

Однако воспользоваться этим законом позиционирования нельзя, так как параметры ξ не только неизвестны, но и могут непредсказуемым образом меняться. Поэтому на втором этапе дополним закон управления (5.20) алгоритмом самонастройки параметров вида

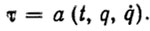(5.21)

В качестве такого алгоритма можно взять любой (в том числе и оптимальный) конечно сходящийся алгоритм решения системы вспомогательных эстиматорных неравенств (5,14). Эти алгоритмы гарантируют после конечного числа коррекций r параметров управления (5.20) выполнение эстиматорных неравенств (5.14) откуда уже непосредственно следует выполнение целевого неравенства (5.18) с некоторым ε.

Процесс адаптации разбивает заданный период движения (t'_k, t_k+1] на интервалы позиционного управления (t_k, t;_k] и интервалы адаптации (t'_k, t_k+1], причем мера последних не превышает величины rθ, где r - оценка сверху на число коррекций алгоритма адаптации (5.21), а θ - время одной коррекции. Отметим, что в интервалах управления параметры закона управления не изменяются, а в интервалах адаптации они корректируются согласно алгоритму самонастройки (5.21).

Оценивая ошибку позиционирования при адаптивном управлении вида (5.20), (5.21), получим

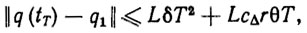(5.22)

где L и c_Δ - параметры. Из оценки (5.22) следует, что достижимая точность позиционирования определяется соотношением

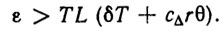(5.23)

Следовательно, за счет выбора параметров адаптивной системы позиционного управления точность приведения рабочего органа в требуемую позицию может быть сколь угодно высокой. Этого можно добиться как с помощью алгоритма адаптации с наименьшим возможным числом коррекций r, так и выбором параметров θ ;и δ из условия минимизации правой части расчетного соотношения (5.23). Заметим, что если точность δ решения эстиматорных неравенств фиксирована, то точность позиционирования тем выше, чем больше скорость сходимости алгоритма адаптации и быстродействие адаптатора, реализующего этот алгоритм.

Другой метод адаптивного позиционирования манипулятора заключается в использовании стабилизирующего закона управления (5.12), где q_p(t)=q₁ в сочетании с алгоритмом адаптации (5.13) вида (5.15). Преимущество этого метода проявляется в том, что в качестве программной траектории q_p(t) здесь берется конечное состояние манипулятора q₁ и, следовательно, отпадает необходимость в ее предварительном расчете [например, по формуле (5.19)]. Достижимая точность позиционирования определяется при этом соотношением (5.17). Исходя из этих расчетных соотношений, легко выбрать приемлемые параметры адаптивной системы позиционного управления.