5.3. Программное обеспечение и цифровое моделирование адаптивного управления манипулятором

Алгоритмы адаптивного программного управления исполнительными приводами и механизмами робота обычно реализуются на ЭВМ. В простейших случаях это может быть микро- или мини- ЭВМ, в сложных - мультимикропроцессорная локальная вычислительная сеть.

Программное обеспечение адаптивных систем управления роботов напоминает по своей структуре и составу операционные системы реального времени для мини- и микроЭВМ. Принцип мультизадачности, используемый в этих системах, позволяет распараллелить вычислительные процессы, связанные с формированием адаптивного программного управления. Эти процессы (алгоритмы) могут выполняться либо на одном процессоре (в этом случае используются специальные средства распределения вычислительных ресурсов), либо на разных процессорах.

Структура адаптивных систем программного управления допускает естественное распараллеливание вычислительных процессов и их мультимикропроцессорную реализацию. Последнее означает, что каждый выделенный процесс (алгоритм) реализуется на своем микропроцессоре. При таком распараллеливании облегчается проектирование программного обеспечения и повышается надежность системы управления.

Остановимся на некоторых особенностях программирования движений роботов с адаптивным управлением. Для этих роботов характерно уменьшение роли и значения ручного обучения, широко используемого в роботах с программным управлением. Более перспективными являются способы аналитического и языкового программирования. Они позволяют автоматически программировать сложные технологические (например, сборочные) операции.

Гибкие алгоритмы программирования, описанные в гл. 2, не только строят и оптимизируют программные движения, но и оперативно корректируют их на основании сигналов датчиков в зависимости от изменения условий эксплуатации робота. Сложнее дело обстоит при программировании роботов с помощью текстового описания требуемых операций на специализированном языке. В качестве такого языка используются либо универсальные языки высокого уровня с соответствующей их модификацией, либо новые языки, специально предназначенные для программирования ро-ботов. Примерами таких языков могут служить языки AML, RPL и VAL [100]. Основные характеристики языков программирования роботов приведены в табл. 5.1.

Важным средством анализа работоспособности и выявления преимуществ адаптивного управления по сравнению с программным является моделирование на ЭВМ. Для упрощения экспериментальных исследований рассмотрим трехзвенный манипулятор, имеющий сравнительно простое математическое описание.

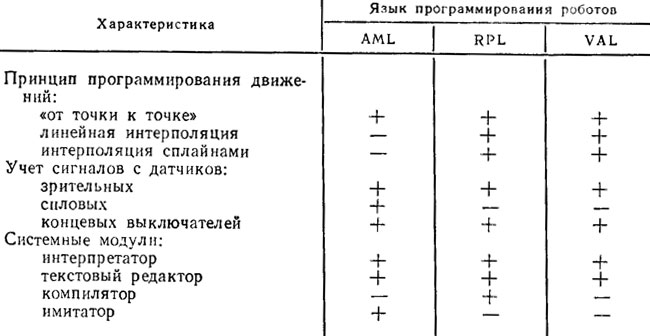
Таблица 5.1

Кинематическая схема манипулятора включает три вращательные пары. Конфигурация манипулятора определяется набором обобщенных координат q=|q_i|³_i=1. а его динамика описывается уравнением вида (5.1), где u=|u_i|³_i=1 - 3-мерный вектор управлений, А(q, ξ)- заданная 3*3-матрица-функция, b(q, 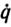, ξ) - заданная 3-мерная вектор-функция зависят от вектора параметров ξ манипулятора и груза. Компонентами вектора параметров ξ являются масса звеньев и груза, длина звеньев, ускорение свободного падения, коэффициенты сухого и вязкого трения в шарнирах и т. п.

Управляемые движения манипулятора определялись путем численного интегрирования уравнений динамики (5.1) при заданных управляющих моментах. В качестве схемы интегрирования был принят метод Рунге-Кутта. Было проведено три серии экспериментов, относящихся к исследованию не адаптивных законов программного управления, описанных в п. 5.1, и адаптивных законов контурного и позиционного управления, предложенных в и. 5.2. В качестве алгоритмов адаптации использовались и моделировались дискретные локально оптимальные конечно-сходящиеся алгоритмы, рассмотренные в п. 3.6 и 3.7.

Пакет программ, реализующий адаптивные законы управления, имеет модульную структуру. Модель "программатор" рассчитывает программную траекторию q_p и ее производные , в соответствии с алгоритмами, описанными в гл. 2, и подает их в модуль "регулятор". 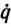Модуль, имитирующий работу информационно-измерительной системы, осуществляет интегрирование уравнений динамики манипулятора и формирование сигналов обратной связи q, , которые подаются в модуль "регулятор", а также сигнала ускорения q, используемого в модуле "эстиматор" для оценки качества управления. При нарушении эстиматорных неравенств производится коррекция параметров закона управления с помощью того или иного алгоритма адаптации, который реализуется в модуле "адаптатор".

Рассмотрим сначала экспериментальные результаты моделирования законов позиционного управления при наличии начальных и неизвестных параметрических возмущений. В этой серии экспериментов исследовались стабилизирующие законы управления вида (5.11). Обобщенные координаты манипулятора измерялись в радианах, время - в секундах, шаг интегрирования уравнений динамики равнялся 10^-3 с. В качестве основных параметров манипулятора были взяты следующие длины и массы звеньев: l₁=0,4 м, l₂=0,3 м, l₃=0,26 м, m₁=10 кг, m₂ = 7 кг, m₃= 3 кг, а масса груза m₀ варьировалась в пределах 0-15 кг. Точность отслеживания программной траектории равнялась 0,05 рад.

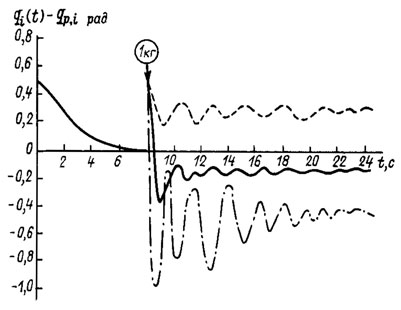
Рис. 5.1. Влияние параметрических возмущений на точность позиционирования при Γ₁ = -2I, Γ₂= -I:

В первой серии экспериментов требовалось перевести манипулятор из заданного начального состояния q(t₀)=(0.76, 0.93, 1.11)^T, (t₀)=(0.5, 0.5, 0.5) в желаемое конечное состояние q(t_T)=(0,26, 0.43, 0.61), 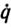(t_T)=(0, 0, 0). В качестве программной траектории было взято q_p(t)=(0.26, 0.43, 0.61)^T.

Сначала предполагалось, что параметрические возмущения отсутствуют, т. е. τ= ξ. Управление формировалось согласно формуле (5.12), где Γ₁=-2I, Γ₂=- I, I - единичная 3*3- матрица. Характер затухания динамической ошибки в процессе позиционирования представлен на рис. 5.1. Как видно из рисунка, динамические ошибки по каждой координате меняются одинаково, что соответствует диагональному виду матриц коэффициентов усиления Γ₁ и Γ₂. В этом случае уравнение динамики манипулятора (5.1), (5.12) распадается на три независимых одинаковых линейных дифференциальных уравнения второго порядка по каждой обобщенной координате. Благодаря этому обеспечивается полная нейтрализация перекрестных связей в каналах управления.

Для уменьшения времени позиционирования (при сохранении апериодического характера затухания динамической ошибки) в тех же условиях моделировался стабилизирующий закон управления (5.12) с диагональными матрицами коэффициентов усиления вида Γ₁=-10I, Γ₂=25I. Характер затухания динамической ошибки в этом случае показан на рис. 5.2. Из сравнения полученных переходных процессов видно, что период позиционирования манипулятора с заданной точностью тем меньше, чем глубже отрицательная обратная связь в законе управления (точнее говоря, чем левее от мнимой оси лежат корни характеристического уравнения, полученного на основе матричных коэффициентов усиления Γ₁, Γ₂). Для матриц Γ₁, Γ₂ из первого эксперимента все корни характеристического уравнения совпадают и равны -1, а для матриц Γ₁ Γ₂ из второго эксперимента они равны -5.

В последующих экспериментах исследовалось влияние параметрических возмущений на точность позиционирования манипулятора при использовании стабилизирующего закона управления без адаптации. Сначала моделировался закон управления с параметрами Γ₁=-2I и Γ₂=-I в условиях, когда уровень параметрических возмущений характеризовался величиной ||τ- ξ||²=20,14, что соответствует захвату манипулятором груза массой в 1 кг.

Графики затухания динамической ошибки по каждой обобщенной координате в данном эксперименте представлены на рис.5.1.

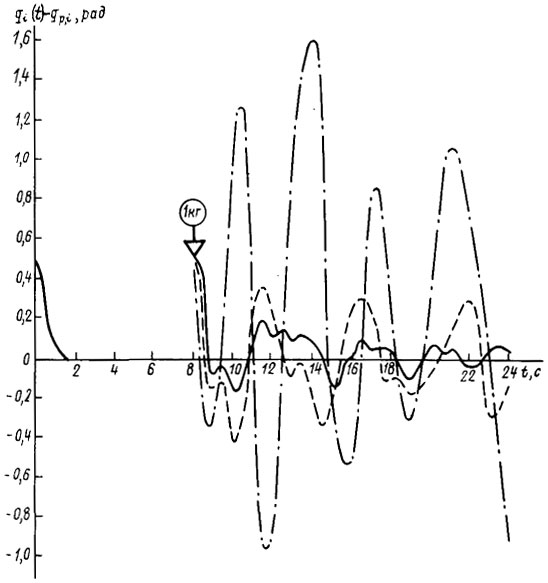
Рис. 5.2. Влияние параметрических возмущений на точность позиционирования при Γ₁=-10I, Γ₂=-25I

Из этих графиков видно, что при наличии параметрических возмущений стабилизирующий закон управления обеспечивает очень грубое (с точностью ε порядка 0,5 рад) позиционирование. При этом точность позиционирования тем больше, чем меньше величина параметрических возмущений.

В следующем эксперименте при том же уровне параметрических возмущений моделировался закон управления (5.12) с параметрами Γ₁=-10I, Γ₂=-25I. Несмотря на увеличение глубины обратной связи по сравнению с предыдущим экспериментом, этот закон управления вообще не обеспечивает позиционирования манипулятора вблизи целевой конфигурации. Вместо этого наблюдаются автоколебания и нарушение конструктивных ограничений, что хорошо видно на рис. 5.2. Дальнейшее увеличение уровня параметрических возмущений в ряде случаев приводило к неустойчивости заданного целевого состояния манипулятора.

В целом проведенные эксперименты свидетельствуют о том, что при достаточно большом уровне параметрических возмущений невозможно подбором параметров Γ₁, Γ₂ закона управления вида (5.12) обеспечить позиционирование манипулятора с заданной точностью. Тем не менее при достаточно малых параметрических возмущениях точное позиционирование возможно.

Целью следующей серии экспериментов было изучение процесса адаптивного позиционирования при большом уровне начальных и параметрических возмущений. В этой серии экспериментов манипулятор внезапно нагружался (или разгружался) различными объектами и, кроме того, время от времени изменялась программная траектория (точнее, изменялись целевые состояния манипулятора).

Моделировался закон управления вида (5.11), неизвестные параметры ξ которого заменялись их оценками τ_k, определяемыми по результатам наблюдений за реальным движением с помощью некоторого алгоритма адаптации вида (5.15). В качестве алгоритма адаптации использовался рекуррентный локально оптимальный конечно-сходящийся алгоритм градиентного (по отношению к эстиматорным неравенствам) типа

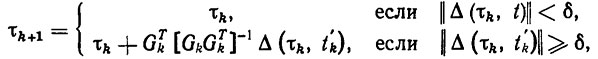(5.24)

где τ₀ - произвольное начальное приближение из множества Q_τ допустимых значений параметров; G_k=G[q(t'_k), 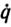(t'_k), 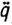(t'_k)], t'_k - первый момент нарушения неравенств || Δ(τ_k,t) ||<δ на k-м интервале управления (t_k,t_k+1], t_k+1=t'_k+θ; θ - параметр, характеризующий быстродействие алгоритма адаптации.

В первом эксперименте рассматриваемой серии требовалось перевести манипулятор из заданного начального состояния q(t₀)=(0.36, 0.53, 0.71)^T, 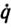(t₀)=(0, 0, 0)^T в желаемое конечное состояние q (t_T) = (0.26, 0.43, 0.61)^T, 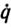(t_T) = (0, 0, 0)^T, которое и было выбрано в качестве программной траектории. В этом и последующих экспериментах в законе управления были взяты матрицы коэффициентов усиления Γ₁=-10I, Γ₂= -25I. Начальные состояния манипулятора в последующих экспериментах совпадали с текущими состояниями в предыдущих экспериментах в момент их окончания, а конечные состояния варьировались. Зависимость обобщенных координат манипулятора от времени в процессе адаптивного позиционирования в рассматриваемой серии экспериментов представлена на рис. 5.3.

Эксперимент начинался с того, что в схват манипулятора помещался груз массой 1 кг. Так как параметры груза неизвестны системе управления, то это эквивалентно действию параметрических возмущений. Однако эти возмущения парировались алгоритмом адаптации и, как видно из рис. 5.3, манипулятор позиционировался в заданной конфигурации с точностью ε= 0,05 рад спустя 10 с. Заметим, что в этом и в последующих экспериментах точность эстиматора δ= 0,01.

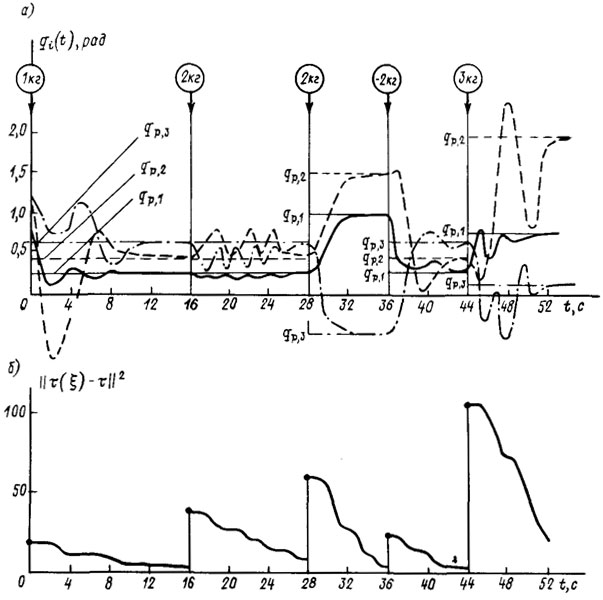
Рис. 5.3. Переходные процессы при адаптивном позиционном управлении: а - процессы позиционирования; б - процессы адаптации

В следующем эксперименте, который начался через 16 с, программная траектория не изменилась, но в схват манипулятора был помещен груз массой 2 кг. Как видно из рис. 5.3, через 12 с процесс позиционирования с заданной точностью завершился.

На 27 с скачком изменилась программная траектория (точнее, изменилось целевое состояние манипулятора). В тот же момент в схват был помещен дополнительный груз массой 2 кг, что привело к скачкообразному возрастанию уровня параметрических возмущений. Процесс позиционирования в новом состоянии завершился через 5 с. На 36 с в новом эксперименте масса груза уменьшилась на 2 кг, и вновь изменилось целевое состояние манипулятора, т. е. изменилась программная траектория. Как видно из рис. 5.3, нужно разгрузить и перевести манипулятор в новое состояние q_p=(0.25, 0.4, 0.6)^T, q_p=(0, 0, 0)^T . Процесс перехода манипулятора в новое состояние завершился через 8 с.

В последнем эксперименте данной серии на 44 с в схват манипулятора был помещен груз массой 3 кг, что привело к увеличению уровня параметрических возмущений. При этом ставилась задача перевода манипулятора в новое состояние q_p= (0.8,2.0,0.1)^T, q_p=(0, 0, 0)^Т. Из рис. 5.3 видно, что время адаптивного позиционирования составило 10 с.

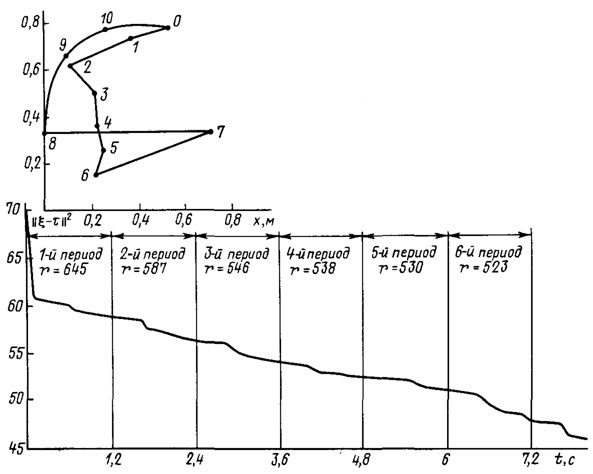
Рис. 5.4. Адаптивное позиционное периодическое управление

Степень неопределенности (и соответственно класс адаптивности) в описанных экспериментах определяется величиной параметрических возмущений 11 - Tfc||2. Важно отметить, что в каждом из рассмотренных экспериментов по адаптивному позиционированию степень неопределенности монотонно убывала. Динамика адаптации (т. е. характер изменения величины ||τ(ξ)-τ_k||²) от эксперимента к эксперименту представлена на нижнем рис. 5.3, а также в табл. 5.2.

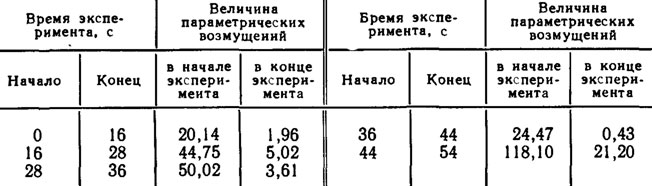
Таблица 5.2

В первом эксперименте требовалось обучить манипулятор осуществлять периодическое движение схвата через последовательность точек, изображенную на рис. 5.4, при наличии больших параметрических возмущений. В этом эксперименте ||ξ - τ₀||²=70, что соответствует грузу в схвате массой 15 кг. После шести периодических движений с последовательным позиционированием схвата в заданных точках процесс адаптации [в силу локального оптимального рекуррентного алгоритма вида (5.24)] завершился по прошествии 7,2 с, в течение которых произошло 3369 коррекций параметров позиционного закона управления. После этого алгоритм адаптации автоматически отключался, а точность позиционирования схвата составляла 2 мм.

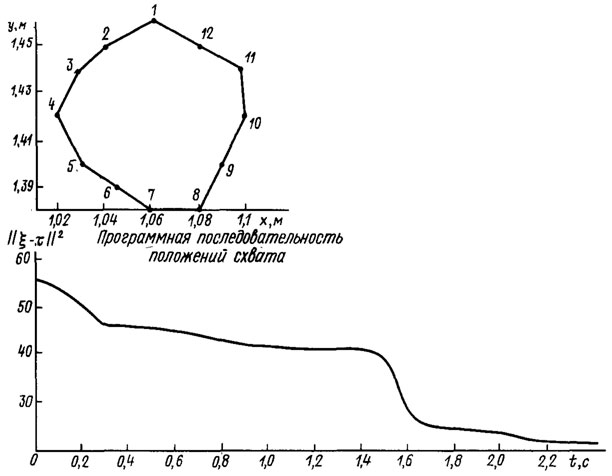
Рис. 5.5. адаптивный обход по контуру

В следующем эксперименте манипулятор частично разгружался (масса груза 8 кг) и требовалось осуществить движение схвата через последовательность точек, изображенных на рис. 5.5. После 1050 коррекций позиционного закона управления алгоритм адаптации отключался, что соответствует 2,4 с реального времени движения манипулятора. Точность позиционирования схвата в заданной последовательности точек составляла 3 мм.

Затем скачком изменялись параметры манипулятора (в частности, масса груза увеличивалась до 16 кг). При этом начальный уровень параметрических возмущений составлял ||ξ - τ₀||²=2110. Как видно из рис. 5.5, процесс адаптации в этом эксперименте завершился через 16 с после 1196 коррекций позиционного закона управления. Точность позиционирования уменьшилась и составила 6 мм.

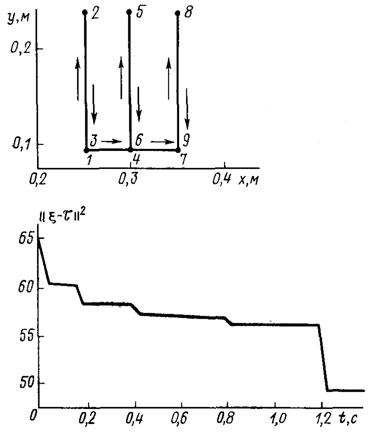
Рис. 5.6. Адаптивный обход заданной последовательности точек

Аналогичные эксперименты по адаптивному позиционированию схвата проводились для различных последовательностей целевых точек

и для разных уровней параметрических возмущений, порождаемых непредсказуемым изменением не только груза, но и других факторов. В заключение опишем эксперимент, целью которого являлся обход схватом нагруженного манипулятора (масса груза 15 кг) заданной последовательности целевых точек в области достижимости, изображенной на рис. 5.6. Уровень начальных параметрических возмущений составил || ξ- τ₀||² = 65, а число коррекций позиционного закона управления (5.20) r= 710. Через 1,3 с точность адаптивного позиционирования при периодическом обходе схватом заданной последовательности точек составила 1 мм.

По результатам проведенных экспериментальных исследований на ЭВМ могут быть сделаны следующие общие выводы.

1. Стабилизирующие законы управления обеспечивают осуществление программной траектории манипулятора лишь при достаточно малом уровне параметрических возмущений. Увеличение уровня параметрических возмущений приводит к потере точности, резкому увеличению колебательности переходных процессов вплоть до потери устойчивости.
2. Адаптивные законы управления обеспечивают надежное позиционирование схвата манипулятора с заданной точностью при любом уровне неизвестных параметрических возмущений. Это достигается благодаря адаптивной коррекции параметров закона управления, причем число коррекций и время адаптации всегда ограничены.