5.4. Адаптивное управление роботом с шаговыми двигателями

Электрические шаговые двигатели являются одним из наиболее перспективных типов исполнительных двигателей для роботов и РТК. Их достоинствами являются возможность непосредственного цифрового управления от ЭВМ, высокое быстродействие и большой вращающий момент.

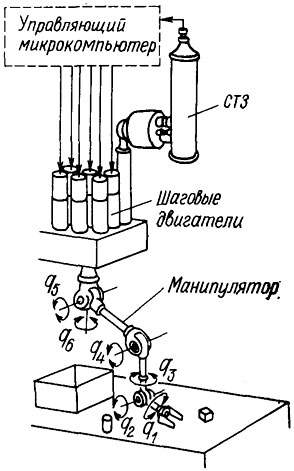
Рис. 5.7. Макет робота-манипулятора с шаговыми приводами

Рассмотрим методику алгоритмического синтеза и опыт программной реализации на ЭВМ адаптивной системы управления манипулятором с шаговыми приводами. Эффективность этой системы по сравнению с традиционными системами программного управления иллюстрируется экспериментальными данными, полученными при ее испытаниях в составе манипуляционного робота, изображенного на рис. 5.7. Этот робот оснащен телевизионной системой зрения на базе промышленной телевизионной установки ПТУ-102, позволяющей воспринимать и анализировать обстановку в рабочей зоне. Благодаря этому обеспечивается принципиальная возможность адаптации к изменяющейся производственной обстановке, в частности, оказывается возможным манипулирование деталями без их предварительного ориентирования и позиционирования.

Основное препятствие на пути широкого применения систем программного управления разомкнутого типа связано с известным эффектом "потери шагов" шагового двигателя. Этот эффект часто возникает в режимах разгона и торможения, когда момент нагрузки может превышать движущий момент двигателя. Он особенно характерен для шаговых приводов манипуляционных роботов, поскольку моменты нагрузки на каждом из двигателей манипулятора существенно зависят от его текущей конфигурации, а основными режимами работы являются разгон и торможение.

Для улучшения качества управления шаговыми приводами роботов целесообразно использовать позиционную обратную связь. Достоинством такой замкнутой импульсной системы программного управления по сравнению с разомкнутой является более высокая помехоустойчивость и стабильность работы в широком диапазоне изменяющихся нагрузок.

Точность работы замкнутых систем программного управления шаговыми двигателями существенно зависит от точности датчиков обратной связи, от упругих деформаций в кинематических передачах, от неконтролируемых параметрических и внешних возмущений. Как показали эксперименты на лабораторном образце робота с шаговыми приводами, точность позиционирования манипулятора существенно снижается при больших моментах нагрузки на выходных валах двигателей, а в некоторых режимах наблюдаются автоколебания. Эти факты находятся в полном согласии с результатами сравнительного анализа влияния параметрических возмущений на динамику манипуляционных роботов для различных систем программного управления, приведенного в п. 5.1. Они свидетельствуют о том, что улучшение качества управления при одновременном расширении диапазона допустимых нагрузок может быть достигнуто путем перехода к адаптивному управлению шаговыми приводами.

Переходя к описанию адаптивной системы программного управления роботом, заметим, что описанные выше алгоритмы контурного и позиционного управления непрерывного типа непосредственно не применимы для управления шаговыми приводами. Поэтому прежде всего опишем дискретную модификацию алгоритмов адаптивного управления, учитывающую импульсный характер работы шаговых приводов.

В качестве конкретного объекта управления служил манипулятор с шаговыми двигателями, изображенный на рис. 5.7. Лабораторный образец этого робота был создан в ЦНИИРТК при Ленинградском политехническом институте им. М. И. Калинина на базе манипулятора типа МЭМ-10М с шестью степенями свободы, в котором силовые сельсины заменены шаговыми двигателями типа ШД-5 [42, 63]. Последние работают от схемы четырехтактной коммутации с импульсной форсировкой.

Управление шаговыми двигателями манипулятора осуществлялось от ЭВМ М-6000. Для организации обратной связи использовались потенциометрические датчики положения, вмонтированные в шарниры манипулятора, и датчики моментов на выходных валах приводов. Кроме того, для "очувствления" схвата манипулятора использовались тактильные и локационные датчики. Связь шаговых двигателей с манипулятором осуществляется через дифференциальную систему передач. Конфигурация манипулятора в каждый дискретный момент времени k определяется вектором обобщенных координат q=|q_i,k|_i=1, k = 0, 1, 2, ..., на компоненты которого наложены конструктивные ограничения вида

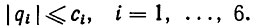(5.25)

Углы поворота v_k выходных валов шаговых приводов определяются величиной управляющего воздействия vk на входе двигателя и величиной N_k силовой обратной связи с манипулятором через дифференциальную систему передач. Последняя определяет некоторую жесткую функциональную зависимость между величинами v_k и q_kt определяемую некоторой невырожденной матрицей передаточных отношений Р. Через дифференциальную систему передач на исполнительные приводы подается нагрузка.

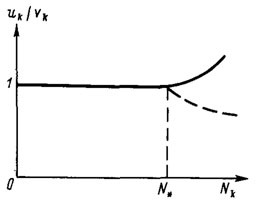
Рис. 5.8. Динамическая характеристика шаговых двигателей

Моменты нагрузки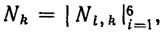
зависящие от конфигурации манипулятора, масс и длин его звеньев, определяются по известным формулам [42, 63].

Работа каждого двигателя под действием управления u_k,i и нагрузки N_k,ii приближенно описывается соотношениями [63]:

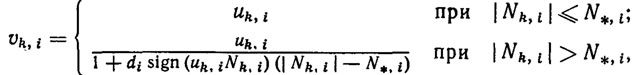(5.26)

где N_*,i - моменты приемистости двигателей; d_i - параметры двигателей.

Характер зависимости u_k/v_k (отношение командного управления u_k к фактически отработанному управлению v_k) от нагрузки N_k по каждой обобщенной координате представлен на рис. 5.8. Согласно графику, при | N_k,i|≤N_*,i имеет место равенство

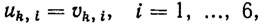(5.27)

что соответствует идеальной работе двигателей независимо от нагрузки N_k,i на их выходных валах. При |N_k,i|>N_*,i величина v_k,i либо больше u_k,i (в случае, если направление момента нагрузки N_k,i совпадает с направлением вращения i-го двигателя под действием управления u_k,i), либо меньше u_k,i (в случае, если направление момента нагрузки N_k,i и вращения i-го двигателя противоположны). Поэтому при моментах нагрузки N_k,i, превышающих по абсолютной величине моменты приемистости двигателей N_*,i, возникает необходимость в коррекции управления таким образом, чтобы парировать "потерю шагов" двигателей и обеспечить требуемую точность позиционирования или отработки программной траектории.

Однако заранее рассчитать приемлемый закон коррекции управления в изменяющихся условиях не представляется возможным. Это связано с тем, что моменты нагрузки на выходных валах двигателей существенно зависят от моментов инерции груза, параметров двигателей и манипулятора, которые могут непредсказуемо изменяться в широком рабочем диапазоне. Поэтому не адаптивный подход к синтезу управления при больших нагрузках на выходных валах шаговых двигателей оказывается неэффективным. Это диктует необходимость введения специальных элементов (алгоритмов) адаптации в систему программного управления, обеспечивающих ее автоматическое приспособление к заранее неизвестным и изменяющимся условиям эксплуатации робота.

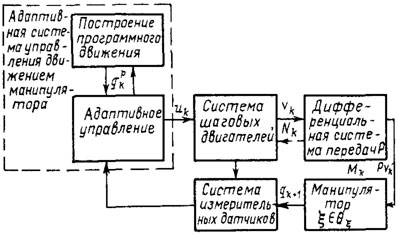
Рис. 5.9. Схема адаптивного управления шаговыми приводами манипулятора

На рис. 5.9 представлена общая схема адаптивной системы программного управления манипулятором с шаговыми приводами рассматриваемого типа. Эта система функционирует следующим образом. Вначале рассчитывается программная траектория q^p_k, k= 0, 1, ..., в соответствии с одним из методов, описанных в гл. 2. Как показали эксперименты на макете, при небольших (до 2 кг) нагрузках в схвате программная траектория отрабатывается достаточно точно. Увеличение нагрузки приводит к существенному снижению точности отработки, к автоколебаниям или даже к выходу манипулятора (по отдельным координатам) на ограничения. Поэтому нарушение условия |N_k,i|≤N_*,i хотя бы по одной из обобщенных координат является сигналом для перехода в режим адаптации.

Переходя к рассмотрению этого режима, запишем уравнения управляемого движения манипулятора с шаговыми приводами в виде:

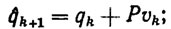
(5.28)

где c_i - параметры, характеризующие конструктивные ограничения по i-й обобщенной координате.

Разрешим это уравнение относительно управления u_k и подставим в полученные соотношения вместо q_k+1 величины q^p_k+1 задающие программную траекторию. Тогда получим идеальный закон управления, который в принципе гарантирует точную от-работку программной траектории. Однако воспользоваться этим законом нельзя, так как он зависит от неизвестных характеристик шаговых двигателей (величины d_i, N_*,i), от параметров манипулятора и груза (величины m_i, r_i, l_i). Тем не менее явный вид идеального управления полезен - он подсказывает общий вид (структуру) законов управления, в классе которых следует синтезировать адаптивное программное управление.

В рассмотренном случае идеальный закон управления имеет вид

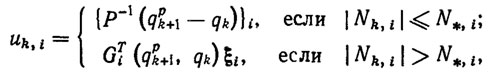(5.29)

где G_i1u, ξ - некоторые заданные вектор-функции, явный вид которых приведен в работах [42, 631. На основании закона (5.29) управление шаговыми приводами манипулятора в адаптивном режиме определим формулой [631

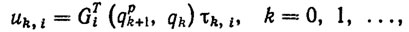(5.30)

где τ_k,i - настраиваемые параметры, трактуемые как оценки неизвестного вектора параметров ξ идеального закона управления (5.29).

В качестве алгоритма настройки параметров, представляющего собой алгоритм адаптации, можно взять рекуррентный или много шаговый оптимальный алгоритм решения системы эстиматорных неравенств вида

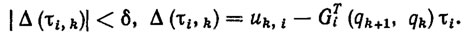(5.31)

Нетрудно убедиться, что неравенства (5.31) разрешимы с "запасом" δ (при τ_i=ξ_i) и что из выполнения этих неравенств, заданных в пространстве управлений, следует выполнение целевых неравенств, заданных в терминах обобщенных координат, а именно:

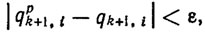(5.32)

где ε=ε(δ) - положительные параметры, характеризующие точность осуществления программной траектории.

Приведем явную формулу локально-оптимального рекуррентного алгоритма адаптации 1421:

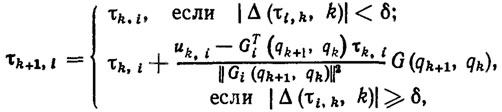(5.33)

где τ_0,i - произвольные начальные оценки неизвестных параметров. Эти алгоритмы гарантируют решение эстиматорных неравенств (5.31), а следовательно, и целевых неравенств (5.33) после конечного числа коррекций параметров адаптивного закона управления (5.30).

Таким образом, синтезированный адаптивный закон управления (5.30), (5.33), использующий обратную связь по текущим положениям q_k манипулятора и информацию о заданной программной траектории q^p_k+1 обеспечивает после некоторого периода адаптации требуемую близость реальной и программной траекторий.

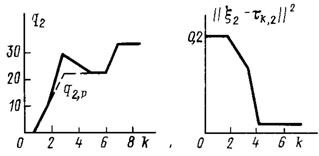
Рис. 5.10. Переходные процессы по координате q₂

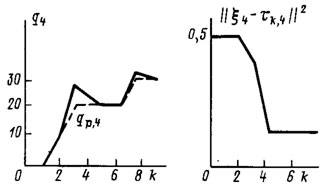
Рис. 5.11. Переходные процессы по координате q₄

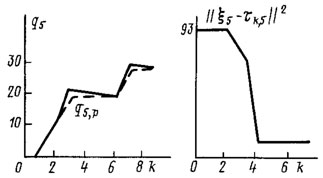
Рис. 5.12. Переходные процессы по координате q₅

Эффективность предложенного алгоритмического обеспечения для адаптивной системы управления шаговыми приводами манипулятора проверялась путем моделирования на ЭВМ. При этом расчет числа управляющих импульсов n_k,i на входе каждого двигателя осуществляется по формуле

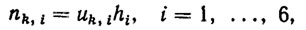(5.34)

где h_i-шаг i-го двигателя. Распределение управляющих импульсов во времени программно осуществлялось так, чтобы отработка всех управляющих воздействий u_k,i (или n_k,i), i= 1, ..., 6 заканчивалась одновременно.

Моделировались управляемые движения манипулятора, соответствующие последовательному перемещению схвата из одной точки рабочего пространства в другую, а также движение по заданной траектории ("поиск, взятие и перенос деталей", "точечная сварка по контуру" и т. п.). Рассмотрим некоторые типичные эксперименты.

В первом эксперименте требовалось перевести манипулятор вместе с помещенным в схват грузом (масса груза 5 кг) в три последовательных положения q⁽¹⁾=(10, 10, 10, 10, 10, 10)^T, q⁽²⁾=(20, 20, 20, 20, 20, 20)^T, q⁽³⁾=(30, 30, 30, 30, 30, 30)^T с точностью ε= 0,1 (величины обобщенных координат задавались в градусах). Параметры m₀, m_i, l_i, d_i, r_i, N_*,i i = 1, ..., 6, груза, манипулятора и шаговых приводов считались либо приближенно известными, либо неизвестными.

На рис. 5.10-5.12 представлены графики (жирная линия) траекторий манипулятора по второй, четвертой и пятой обобщенной координатам (в рассматриваемом эксперименте именно по этим координатам осуществлялась адаптивная коррекция параметров управления). На тех же рисунках графики справа характеризуют собственно процесс адаптации по этим обобщенным координатам в терминах изменения расстояния от вектора текущей оценки параметров τ_k,i адаптивного управления до неизвестного вектора параметров ξ_i идеального закона управления. Как видно из этих графиков, в процессе отработки программной траектории по каждой обобщенной координате было сделано не более четырех коррекций управления.

В другой серии экспериментов моделировался процесс точечной сварки по контуру. Так, в одном из экспериментов требовалось перевести схват последовательно в шесть точек, расположенных на окружности. При использовании сварочной головки массой 2 кг реализовывался не адаптивный режим управления, характеризующийся тем, что |N_k,i|≤N_*,i по всем обобщенным координатам. В этом случае система управления осуществила периодическое перемещение схвата манипулятора во все шесть заданных позиций с точностью ε=1 мм. По мере увеличения нагрузки в схвате до 5 кг реализовывался адаптивный режим управления, для которого |N_k,i|>N_*,i хотя бы по одной обобщенной координате. При точности позиционирования ε= 1 см произошло не более двух коррекций управления по различным обобщенным координатам, а при точности ε= 1 мм - не более четырех коррекций. Дальнейшее увеличение нагрузки в схвате манипулятора приводило либо к увеличению числа коррекций адаптивного управления (до нескольких десятков коррекций), либо к нарушению конструктивных ограничений на управление.

В целом результаты моделирования адаптивной системы программного управления шаговыми двигателями манипуляционного робота свидетельствуют о ее эффективности и возможности простой программно-аппаратной реализации на базе управляющих микроЭВМ или микропроцессоров. Введение элементов (алгоритмов) адаптации в систему программного управления расширяет функциональные возможности и повышает надежность роботов с шаговыми приводами.