5.5. Адаптивное управление роботами с двигателями постоянного тока

Широкий класс роботов приводится в движение с помощью двигателей постоянного тока. Примерами таких роботов могут служить промышленные манипуляционные роботы типа ТУР-2,5, ТУР-10, РПМ-25, "Пума" (Рита), "Прагма" (Pragma) и т. п., исследовательские роботы типа ЛПИ-2, УЭМ-5МВТУ, а также ряд транспортных роботов.

Достоинствами приводов на базе двигателей постоянного тока являются хорошие динамические характеристики (высокие точность и быстродействие), сравнительно большой КПД (порядка 0,6), компактность и простота эксплуатации. Использование электрических приводов в промышленных приводах и РТК стимулируется также широким распространением и дешевизной электрических источников питания.

Управление двигателями постоянного тока обычно осуществляется с помощью электрического напряжения приложенного к обмотке якоря. Динамика таких двигателей описывается системой уравнений вида:

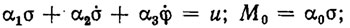(5.35)

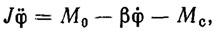(5.36)

где σ - сила тока в обмотке якоря; φ - скорость вращения вала двигателя; М₀ - вращающий момент; J - момент инерции вращающихся масс, приведенный к ротору двигателя; β - коэффициент вязкого трения; М_c - момент сопротивления; α₀, α₁, α₂, α₃ - параметры двигателя.

Исключая из уравнений (5.35) и (5.36) промежуточную переменную σ, получим уравнение динамики двигателя постоянного тока в следующем виде:

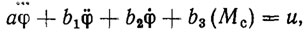(5.37)

где

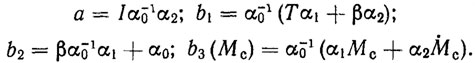
Для увеличения мощности двигателей и получения больших вращающих моментов применяются разного рода преобразователи и электромашинные усилители. Вращение вала двигателя с помощью механизма передачи движения (редуктора) преобразуется во вращение выходного вала, на котором закрепляется соответствующее звено исполнительного механизма (манипулятора).

Двигатель совместно с редуктором образует силовой электромеханический модуль. Схема такого модуля представлена на рис. 5.13, где приняты следующие обозначения: Р - передаточное число редуктора; c - жесткость упругого вала; М - вращающий момент на выходном валу; q - угол поворота выходного вала (обобщенная координата). Для силовых модулей роботов характерны нелинейные эффекты, порождаемые насыщением магнитного потока, силами сухого и вязкого трения, упругостью и люфтами в редукторах.

Важным преимуществом двигателей постоянного тока является то обстоятельство, что на их основе (путем соответствующей конструктивной модификации) могут создаваться моментные двигатели. Такие двигатели особенно перспективны в робототехнике, поскольку они непосредственно (без редуктора) передают развиваемый вращающий момент на исполнительный механизм. Благодаря этому увеличивается механическая жесткость и упрощается система управления роботом.

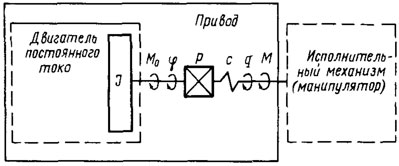
Рис. 5.13. Схема силового электромеханического модуля робота

Объединяя уравнения динамики электрических приводов (5.37) с уравнениями движения манипулятора (5.1), получим полное описание динамики электромеханического робота в следующем виде:

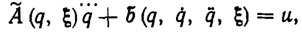(5.38)

где Ã и 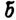- заданные матрица-функция размерности т*т и вектор-функция размерности m, непосредственно выражаемые через матрицу-функцию А, вектор-функцию b в уравнении (5.1) и параметры уравнений динамики приводов (5.37). Заметим, что матрица Ã (q, ξ) не вырождена при всех возможных значениях q и ξ. Из этого факта следует разрешимость уравнения динамики (5.38) относительно старшей производной 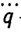, а значит, и возможность цифрового моделирования управляемых движений робота путем численного интегрирования уравнения (5.38).

Цель программного управления роботом заключается в обеспечении требуемой точности воспроизведения заданной программы движения (ПД) манипулятора. Для ее достижения необходимо прежде всего синтезировать соответствующий закон управления электрическими приводами.

Простейшим способом управления по заданной программе является программное управление, используемое в некоторых промышленных роботах первого поколения. Аналитическая запись программного управления с учетом динамики робота имеет вид, аналогичный закону управления (5.2). При реализации такого управления в роли датчика выступает таймер, который последовательно шаг за шагом формирует управляющие воздействия на двигатели.

В ходе программного управления не используются сигналы обратной связи о текущем состоянии двигательной системы робота и внешней среды. Поэтому в таких системах программного управления отсутствует подтверждение фактической отработки ПД. Другим недостатком этих систем является жесткий характер управления. В связи с этим для обеспечения работоспособности роботов с программным управлением нужны специальная технологическая оснастка и организация неизменных условий их эксплуатации. Создание и поддержание таких условий требует значительных дополнительных затрат, сравнимых со стоимостью робота.

Более эффективным способом управления манипуляционными роботами является сервоуправление по программе. В его основе лежит идея отработки ПД с помощью сервоприводов, использующих обратную связь по фактическому состоянию манипулятора. При этом коэффициенты усиления в каналах обратной связи за-ранее рассчитываются так, чтобы обеспечить воспроизведение ПД с заданной точностью при наличии небольших начальных и параметрических возмущений.

В современных промышленных роботах сервоуправление по программе обычно реализуется с помощью серийно выпускаемых сервоприводов с локальными обратными связями по положению и скорости. Двигательная система таких роботов представляет собой манипулятор с т обобщенными координатами q₁, ..., q_m по каждой из которых действует свой сервопривод. Задача i-го сервопривода заключается в том, чтобы, используя обратную связь по q_i(t), 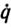_i(t) обеспечить отработку программной "уставки" q_p,i(t) с заданной точностью.

Поскольку исполнительный механизм (манипулятор) вместе с грузом является общей нагрузкой по отношению ко всем сервоприводам, двигательную систему робота следует рассматривать как многосвязную систему с перекрестными связями. Такая система включает m взаимосвязанных подсистем. На вход i-й подсистемы подается i-я компонента ПД q_p,i(t), а выходом служит реальное значение обобщенной координаты q_i(t). Взаимодействие подсистем происходит по каналам перекрестных связей.

В практике проектирования сервоприводов для промышленных роботов широко применяется упрощенный метод расчета, основанный на выделении отдельных подсистем без учета явлений динамического взаимодействия [7, 16, 70]. Такой подход позволяет расчленить многосвязную систему, движения которой в общем случае описываются нелинейными дифференциальными уравнениями высокого порядка вида (5.38), на m сравнительно простых локальных систем.

Для упрощения расчетов уравнения движения каждой подсистемы линеаризуют в окрестности соответствующей компоненты ПД, а коэффициенты полученного нестационарного линейного дифференциального уравнения "замораживают" [70]. При этом предполагается, что переходные процессы в замкнутой двигательной системе протекают настолько быстро, что ПД, а следовательно, и коэффициенты линеаризованного уравнения не претерпевают значительных изменений.

Описанный приближенный метод расчета сервоприводов для промышленных роботов, несмотря на отсутствие строгого обоснования, на практике зачастую обеспечивает требуемую точность отработки ПД и приемлемое качество управления. Поэтому он используется при проектировании многих промышленных роботов с позиционными и контурными системами управления.

На рис. 5.14 представлена структурная схема сервоуправления по программе с помощью сервоприводов, приводящих в движение исполнительный механизм робота. Здесь приняты следующие сокращения:

ЦАП - цифроаналоговый преобразователь;

УС - усилитель сигнала;

ШИП - широтно-импульсный преобразователь;

УМ - усилитель мощности;

ДПТ - двигатель постоянного тока;

РД - редуктор;

ТГ - тахогенератор;

ДП - датчик положения и обозначения: k_i, i = 0, 1, ..., 6, - коэффициенты передачи соответствующих элементов схемы; 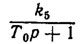- передаточная функция ТГ; Т₀ - постоянная времени ТГ;р=d/dt оператор дифференцирования.

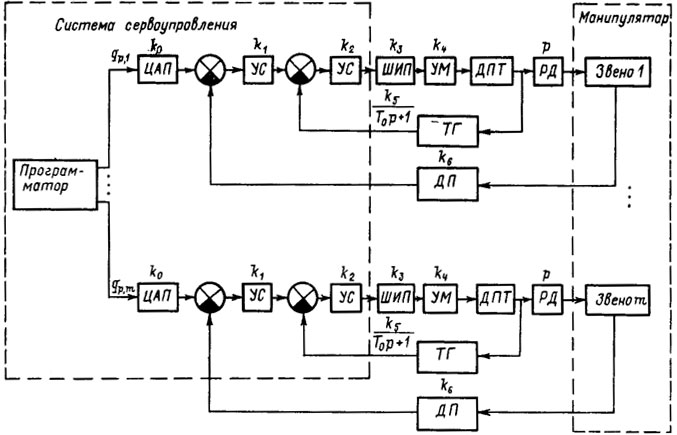
Рис. 5.14. Схема локального сервоуправления по программе

ПД q_p(t) формируется специальным программно-временным устройством - программатором, который обычно реализуется на микроЭВМ или на микропроцессоре.

При синтезе локального сервоуправления обычно используются линейные пропорциональные, интегральные, дифференциальные регуляторы или их комбинация - так называемые ПИД-регуляторы. Структура ПИД-регулятора определяется формулой (5.8). Рассмотрим частные случаи такого ПИД-регулятора.

Пропорциональный регулятор формирует управляющее воздействие (в данном случае управляющее напряжение в цепи якоря ДПТ) u_i, пропорциональное ошибке регулирования Δq_i(t)=q_i(t)-q_p,i(t), т. e. отклонению выходной координаты q_i(t) от ее программной "уставки" q_p,i(t):

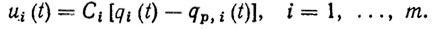(5.39)

Коэффициенты усиления c_i определяют чувствительность регулятора. Увеличение коэффициентов усиления обычно благоприятно влияет на качество управления и, в частности, на точность и быстродействие. Однако при очень больших значениях коэффициента усиления возможны автоколебания или даже потеря устойчивости ПД.

Для улучшения качества переходных процессов в закон управления наряду с ошибкой регулирования Δq_i(t) часто вводят производные Δ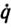_i(t), Δ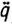_i(t) и т. д. Так, в схеме, изображенной на рис. 5.14, используется пропорционально-дифференциальный (ПД) регулятор вида

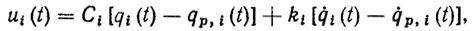(5.40)

где c_i, k_i - коэффициенты усиления в каналах обратной связи. Реализация таких регуляторов требует только датчиков положения и скорости.

Учет динамических особенностей двигателей (и, в частности, учет их инерционности) приводит к необходимости создания интегральных регуляторов, у которых управляющее воздействие пропорционально интегралу по времени от ошибки регулирования. В простейшем случае интегральный регулятор имеет вид

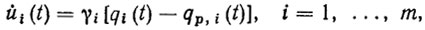(5.41)

где γ_i - коэффициенты усиления. Если же регулирование осуществляется на основе обратной связи по второму, третьему и т. д. интегралу от ошибки Δq_i(t), то соответствующие регуляторы называются регуляторами со вторым, третьим и т. д. порядком астатизма. Обычно увеличение порядка астатизма позволяет повысить точность воспроизведения ПД. Однако при этом может уменьшиться запас устойчивости в замкнутой системе управления.

Регулятор, реализованный в схеме локального сервоуправления манипулятором, изображенный на рис. 5.14, описывается дифференциальным уравнением вида

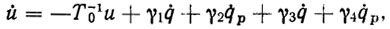(5.42)

где γ₁, γ₂, γ₃, γ₄ - параметры, выражающиеся через коэффициенты передачи k₀, k₁, k₂, k₃, k₄, k5, k₆ и постоянную времени T₀. Ввиду единообразия уравнений серворегуляторов для всех приводов индексы каналов управления в (5.42) опущены.?

Для получения уравнения замкнутой системы управления нужно продифференцировать уравнение динамики (5.38) и подставить в полученное выражение (5.42). В результате получим нелинейное дифференциальное уравнение четвертого порядка относительно вектора обобщенных координат q=(q₁, ..., q_m)^T. Анализ этого уравнения показывает, что подбором постоянной времени ТГ, передаточного числа редуктора и коэффициентов передачи основных элементов системы управления, изображенной на рис. 5.14, можно обеспечить лишь устойчивость ПД q_p(t) в малом, т. е. при достаточно малых начальных возмущениях. Такая система программного управления весьма чувствительна к сколько-нибудь значительным параметрическим возмущениям, что отрицательно сказывается на характере переходных процессов (ухудшаются точность и быстродействие). Другим существенным недостатком этой системы является взаимное влияние каналов локального сервоуправления ввиду того, что все приводы работают на общую нагрузку.

Наилучшими техническими характеристиками в классе рассматриваемых линейных регуляторов обладают комбинированные ПИД-регуляторы вида (5.8). Однако и им присущи недостатки, рассмотренные в п. 5.1. Отсюда ясна необходимость разработки более совершенных систем программного управления, свободных от недостатков локальных серворегуляторов. Эти системы должны учитывать в явном виде (т. е. в структуре регулятора) динамику исполнительных приводов и механизмов робота. Такие системы могут обеспечить любой желаемый характер переходных процессов при отработке заданного ПД.

Рассмотрим новый класс регуляторов, синтезируемых исходя из требования: обеспечить наперед заданный характер ПП в замкнутой динамической системе робота. Отличительной чертой этого класса является то, что при выборе структуры регулятора используются полные (а нелинеаризованные) уравнения динамики. В результате структура регулятора оказывается вполне адекватной структуре динамической модели робота.

Законы управления, реализуемые такими регуляторами, будем называть динамическими. Они решают не только задачу стабилизации ПД с заданным качеством, но и задачу управления конечным состоянием, т. е. задачу перевода манипулятора из любого начального состояния в желаемое конечное за заданное время.

Перейдем к синтезу динамического регулятора в терминах управления напряжением в якорных обмотках двигателей. Введем блочную матрицу коэффициентов усиления в каналах обратной связи вида

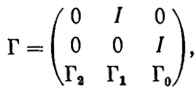(5.43)

где I, 0 - единичная и нулевая матрицы размерности т*т, а Γ₀, Γ₁, Γ₂ - матрицы размерности т*т такие, что матрица (5.43) устойчива (гурвицева). Тогда, очевидно, регулятор вида

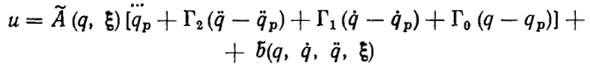(5.44)

обеспечивает асимптотическую устойчивость в целом ПД, т. е.

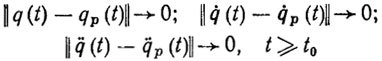(5.45)

при любом уровне начальных возмущений.

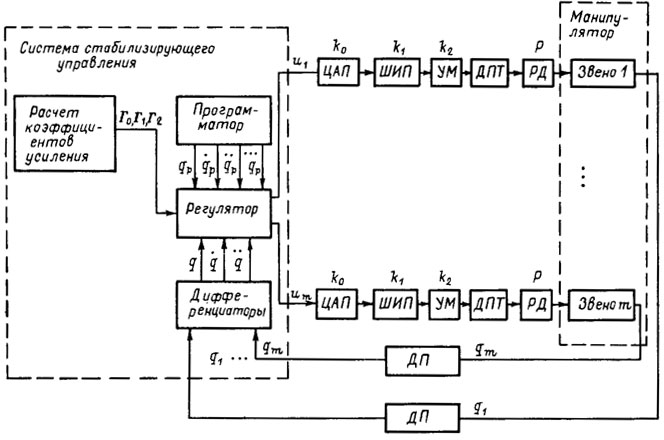
Рис. 5.15. Схема стабилизирующего управления программным движением

Характер переходных процессов в замкнутой системе (5.38), при этом целиком определяется выбором матричных коэффициентов усиления Γ₀, Γ₁, Γ₂. Поэтому желаемое качество управления задается конструктором на стадии параметрического синтеза регулятора вида (5.44).

Структурная схема одного из возможных вариантов технической реализации динамического регулятора (5.44) представлена на рис. 5.15. В отличие от схемы сервоуправления, изображенной на рис. 5.14, здесь используются только обратные связи по обобщенным координатам q₁, ..., q_m подаваемые в микроЭВМ, на базе которой строится регулятор (5.44). При этом на микроЭВМ возлагаются функции программатора (вычисление q_p , q_p, q_p, q_p), дифференциатора (вычисление 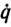, 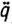) и расчета коэффициентов усиления Γ₀, Γ₁, Γ₂.

Приведем простые расчетные соотношения для выбора параметров (матричных коэффициентов усиления) Γ₀, Γ₁, Γ₂. Для нейтрализации перекрестных связей в каналах, управления выберем эти матрицы диагональными, а именно:

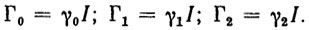(5.46)

Тогда условие устойчивости блочной матрицы (5.43) определяется следующей системой неравенств:

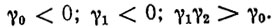(5.47)

Выбирая параметры γ₀, γ₁, γ₂ из этих условий, можно обеспечить не только асимптотическую устойчивость ПД в целом, но и любой желаемый запас устойчивости. Последнее особенно важно с точки зрения придания динамическому регулятору (5.45) свойства нечувствительности (инвариантности) по отношению к действию параметрических возмущений. Ясно, что чем больше уровень параметрических возмущений, тем больший запас устойчивости у регулятора (5.44) нужно предусмотреть.

Следует, однако, иметь ввиду, что без самонастройки параметров регулятора обеспечить наперед заданный характер переходных процессов в этих условиях, вообще говоря, не удается. В то же время параметрические возмущения практически неизбежны. Они обусловлены тем, что точные значения параметров робота и груза ξ могут отличаться от паспортных данных и обычно неизвестны. Более того, они могут дрейфовать в процессе эксплуатации робота непредсказуемым образом. Поэтому возникает необходимость дополнить синтезированный регулятор средствами адаптации (самонастройки).

Для расчета и проектирования адаптивной системы программного управления можно воспользоваться методом, описанным в гл. 3. Согласно этому методу на первом этапе конструируется динамический регулятор вида (5.47), который является идеальным, если предположить, что параметры ξ полностью известны. Заметим, что этот регулятор использует обратные связи по обобщенным координатам q, скорости 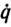и ускорению 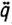их изменения, которые легко реализовать с помощью соответствующих датчиков или функциональных преобразователей (дифференциаторов или интеграторов).

На втором этапе нужно, исходя из единых требований к процессам управления и адаптации, синтезировать эстиматор и адаптатор. Точнее, нужно сконструировать соответствующие эстиматорные неравенства и алгоритмы адаптации, т. е. конечно-сходящиеся алгоритмы решения этих неравенств относительно настраиваемых параметров регулятора. Полученный таким образом адаптивный регулятор обеспечивает приемлемый (желаемый) характер переходных процессов практически при любом уровне неконтролируемых параметрических возмущений.

Приведем формулы, определяющие структуру и явный вид адаптивной системы программного управления электрическими приводами робота. С этой целью прежде всего представим левую часть уравнения динамики робота (5.40) в следующем виде:

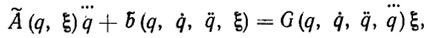
где G - матрица-функция размерности m*p; ξ - р-мерный вектор (в общем случае, вектор-функция), определяемые данным представлением.

Адаптивный регулятор определяется формулой

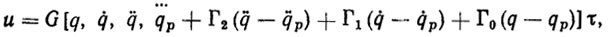(5.48)

где τ - оценка неизвестного вектора параметров ξ, определяемая с помощью некоторого алгоритма адаптации.

Для анализа качества переходных процессов при адаптивном управлении (5.48) сконструируем эстиматорные неравенства вида

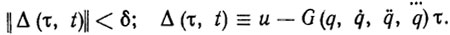(5.49)

Эти неравенства аналогичны неравенствам (5.14): они разрешимы с "запасом" γ при τ= ξ и выпуклы по τ. Поэтому для их решения непосредственно применимы дискретные и непрерывные алгоритмы адаптации, рассмотренные в гл. 3.

Простейший локально-оптимальный рекуррентный алгоритм адаптации имеет вид

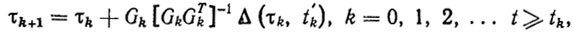(5.50)

где t'_k - первый момент нарушения неравенств (5.49) при τ=τ_k, причем τ_k+1=t'_k +θ; Gk =G [q(t'_k), 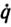(t'_k), 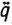(t'_k), 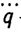(t'_k)], где θ - время, необходимое для вычисления новой оценки τ_k+1 по старой τ_k. Алгоритм (5.50) является конечно-сходящимся, т. е. число коррекций параметров регулятора (5.48) в силу алгоритма самонастройки (5.50) не превышает некоторое натуральное число r . Это означает, что время адаптации конечно и удовлетворяет следующей оценке: μ≤rθ. Используя эту оценку, легко получить (в соответствии с методикой, изложенной в гл. 3) оценку качества переходных процессов.

Синтезированная система адаптивного управления электрическими приводами манипуляционных роботов допускает простую программно-аппаратную реализацию на базе микроЭВМ и микропроцессоров. Один из вариантов такой реализации иллюстрируется на рис. 5.16.

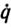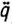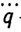Приведенная схема имеет ряд принципиальных отличий от традиционной системы локального сервоуправления по программе, изображенной на рис. 5.14. Во-первых, вместо программных уставок q_1,p ,…, q_m,p подаваемых на вход каждого сервопривода в системе адаптивного управления используется программная траектория q_p и ее производные _p, _p,_p, которые формирует программатор и подает в регулятор. Во-вторых, вместо локальных обратных связей по положению и скорости, охватывающих каждый сервопривод, здесь используется только обратная связь по положению, сигналы q₁,…, q_m которой подаются через аналого-цифровые преобразователи в микроЭВМ или на микропроцессор, осуществляющие их трехкратное дифференцирование. Сигналы обратной связи используются не только в регуляторе, но и в эстиматоре, и адаптаторе. Последние обеспечивают автоматическую коррекцию (самонастройку) параметров регулятора при внезапном изменении нагрузки или при непредсказуемом дрейфе параметров двигательной системы робота.

Рис. 5.15. Схема стабилизирующего управления программным движением

Указанные структурно-функциональные изменения в системе программного управления придают ей качественно новое свойство - высокоразвитую способность адаптации к любым изменениям параметров робота или условий его функционирования. Благодаря этому удается существенно улучшить основные показатели качества управления (точность, быстродействие и т. п.) и расширить функциональные и адаптационные возможности манипуляционного робота.

В некоторых случаях может оказаться целесообразной иная реализация адаптивной системы управления, основанная на использовании обратных связей в терминах физических переменных, непосредственно измеряемых датчиками. Обычно в роли таких переменных выступают обобщенные координаты q=| q,…, q_m|^T скорости их изменения и ток в якорных обмотках двигателей . Обозначим через z 3m-мерный вектор физических переменных, Этот вектор связан с каноническим вектором состояний 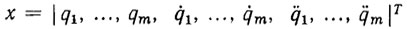линейным невырожденным преобразователем вида

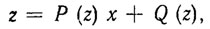(5.51)

где P - некоторая матрица-функция размерности 3m*3m; Q - 3m-мерная вектор функция.

Соотношение (5.51) можно использовать для синтеза идентификатора состояний. Последний, очевидно, описывается формулой

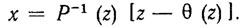(5.52)

На практике размерность вектора физических переменных z в ряде случаев меньше размерности вектора состояний x. При этом идентификатор (5.52) непригоден и приходится конструировать идентификатор более сложной структуры. Такие идентификаторы называются наблюдателями [19, 58].

Алгоритмическое и программное обеспечение адаптивной системы управления представляет собой одну из самых сложных и дорогостоящих компонент робота. Поэтому проектирование программного обеспечения для адаптивного робота требует не только больших интеллектуальных затрат проектировщика, но и адекватных вычислительных средств. Мощность этих инструментальных средств автоматизированного расчета и проектирования должна превышать мощность вычислительной системы, реализующей адаптивное управление конкретным роботом.

На инструментальные средства автоматизированного проектирования возлагаются разнообразные функции: исследование гибких алгоритмов программирования движений манипулятора и адаптивных законов управления приводами; имитационное моделирование переходных процессов; анализ качества управления и т. п. Программное обеспечение многоцелевых инструментальных комплексов состоит из двух компонент: универсальной и специализированной. Универсальная компонента, включающая операционную систему реального времени, предоставляет разработчику различные средства автоматизированного проектирования. К ним относятся интерпретаторы, редакторы, загрузчики и т. п. Специализированная компонента строится на базе универсальной и является проблемно-ориентированной. Она содержит программные средства для имитационного моделирования систем управления.

Пакет программ, служащий для оценки эффективности и сравнения различных систем программного и адаптивного управления манипуляционных роботов с электрическими приводами, описан в п. 3.9. Этот пакет имеет модульную структуру и позволяет моделировать управляемые движения роботов при различных типах программаторов, регуляторов, эстиматоров и адаптаторов. Структура пакета программных модулей представлена на рис. 3.3. На основе разработанного программного обеспечения были проведены эксперименты по имитационному моделированию и сравнительному анализу различных систем управления одним и тем же роботом. Одна из серии экспериментов касалась манипуляционного робота типа ЛПИ-2.

Рассмотрим типичный эксперимент. Моделирование осуществлялось на ЭВМ ЕС-1045 с шагом численного интегрирования (с помощью метода Рунге-Кутта) h= 0,1 с и δ=10^-5. В ходе экспериментов варьировались в широком диапазоне массо-инерционные характеристики груза, силы вязкого трения, упругие деформации в редукторах, электрические параметры двигателей и т. п. Цель управления заключалась в переводе манипулятора из неподвижной начальной конфигурации q₀ в желаемую конечную q₁. В качестве ПД было взято x_p(t)=| q₁, 0, 0|^T, а в качестве регулятора - закон управления (5.44) с параметрами

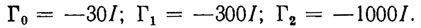(5.53)

При этом блочная матрица коэффициентов усиления (5.43) устойчива и имеет одинаковые собственные числа, равные -10. Последнее число характеризует запас устойчивости такой системы.

Если все параметры ξ известны, то регулятор (5.44) обеспечивает желаемый вид переходного процесса, изображенный на рис. 5.17, а штрих-пунктирной линией. Если же масса груза и другие компоненты вектора параметров ξ неизвестны, то переходный процесс под действием регулятора (5.44), рассчитанного на "номинальную" нагрузку (соответствующую грузу массой 0,5 кг), ухудшается. На рис. 5.17, а он изображен штриховой линией и наглядно демонстрирует снижение точности и быстроты позиционирования. Причиной этого являются параметрические возмущения. Для их компенсации использовался адаптивный закон управления вида (5.48), (5.53), причем в качестве алгоритма адаптации использовался рекуррентный локально-оптимальный алгоритм (5.50). Как видно из рис. 5.17, а, где переходный процесс изображен сплошной линией, требуемая точность позиционирования балы достигнута через 5,5 с. Процесс адаптации характеризуется графиком, показанным на рис. 5.17, б, откуда видно, что уровень параметрических возмущений по мере адаптации монотонно уменьшается.

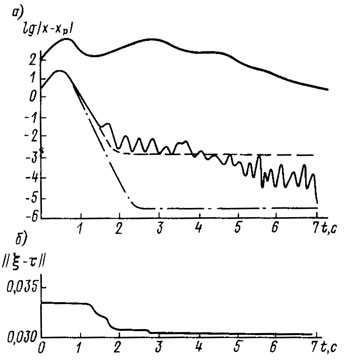
Рис. 5.17. Сравнительный анализ качества систем программного управления: а - переходные процессы; б - процесс адаптации

В целом эксперименты по моделированию различных систем управления показали преимущества адаптивных систем по сравнению с системами, использующими динамические регуляторы или серворегуляторы без самонастройки. Эти преимущества проявились в увеличении точности, надежности и быстроты отработки программной траектории при наличии неконтролируемых помех, а также в снижении чувствительности системы управления к параметрическим возмущениям.