8.5. Адаптивное управление координатными измерениями

Характерная особенность функционирования КИР заключается в том, что целый ряд параметров и условий, определяющих динамику процесса измерений, заранее неизвестен и может непредсказуемо изменяться в ходе управления. К неопределенным параметрам и нестационарным условиям можно отнести упругие деформации и силы трения в исполнительных механизмах, естественный разброс и дрейф характеристик приводов, параметры измеряемой детали, разного рода помехи и неконтролируемые возмущения.

Одним из наиболее эффективных средств компенсации имеющейся неопределенности и постоянно действующих возмущений является адаптивное программирование и управление КИР. Важным преимуществом КИР с адаптивным управлением является, в частности, возможность компенсации неблагоприятного влияния на точность измерений массы аттестуемой детали, а также масса вертикальной каретки вместе с устанавливаемой на ней совокупностью измерительных головок со сменными механическими, оптическими и электронными наконечниками. Это достигается за счет некоторого усовершенствования структуры системы управления и самонастройки ее параметров. Благодаря такой адаптивной нейтрализации действия указанных динамических факторов отпадает необходимость в сложных электромеханических и пневматических противовесах, используемых во многих КИМ и КИР.

Переход от традиционного программного управления к более совершенному адаптивному (а в перспективе и к интеллектуальному) управлению КИР требует автоматизации как процесса программирования измерений с учетом метрологических требований и технологических условий, так и процесса управления программой с заданным качеством ее отработки в изменяющейся производственной обстановке. Рассмотрим особенности синтеза адаптивного управления процессом координатных измерений на примере КИР УИМ-28, разработанного Ленинградским оптико-механическим объединением им. В. И. Ленина [62], В состав КИР УИМ-28 входит управляющий вычислительный комплекс и собственно измерительная машина, включающая измерительную головку, исполнительные механизмы и систему электрических приводов со встроенными датчиками сигналов обратной связи. Управляющий вычислительный комплекс представляет собой стойку управления на базе микроЭВМ с необходимым программным обеспечением, средства цифровой индикации и алфавитно-цифровое печатающее устройство.

Управление КИР УИМ-28 может производиться как в ручном, так и в автоматическом режимах. Ручное управление применяется в процессе наладки и обучения КИР требуемым измерительным операциям. В процессе измерения управление координатными перемещениями измерительной головки осуществляется по заданной программе в автоматическом режиме,

Процесс управления заключается в наведении измерительной головки в контрольные точки, в перемещении по заданной программе или в отслеживании детали по контуру. Считывание координат точек касания измерительного наконечника с аттестуемой поверхностью детали осуществляется автоматически в процессе движении, т. е. без остановок измерительной головки. По результатам координатных измерений рассчитываются действительные размеры аттестуемой детали и их отклонения от номинальных (эталонных) значений. Протокол автоматических измерений выдается с помощью алфавитно-цифрового печатающего устройства "Консул".

По своим техническим характеристикам УИМ-28 является универсальным прецизионным КИР с широкими функциональными и адаптационными возможностями. Точность измерений лимитируется разрешающей способностью датчиков (около 0,2 мкм),в качестве которых используются лазерные интерферометры. Скорость координатных перемещений составляет 0,025-25 мм/с, область достижимости (пределы координатных перемещений) - 315*160*160 мм³. Масса измеряемых деталей не должна превышать 75 кг.

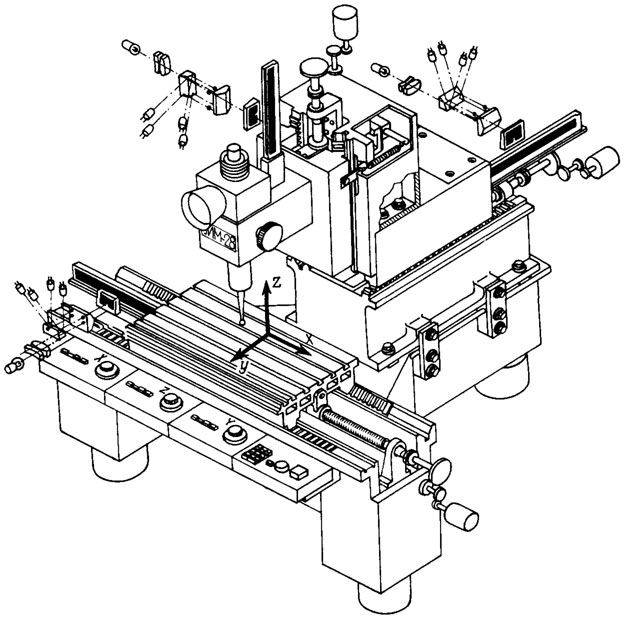
Рис. 8.12. Конструкция КИР

Конструкция КИР УИМ-28 видна из рис. 8.12. В ее состав входит жесткая Т-образная станина, имеющая направляющие с роликами. По этим направляющим перемещается вдоль оси Ох каретка-стол, несущая измеряемую деталь. Перпендикулярно к оси Ох в горизонтальной плоскости на станине закреплена жесткая стойка. Она имеет направляющие с роликами по которым перемещается вдоль оси Оy каретка, несущая на себе жесткую стойку с вертикальными направляющими того же типа. По вертикальным направляющим перемещается вдоль оси Оz каретка с устройством для установки измерительной головки. Все каретки приводятся в движение с помощью однотипных двигателей постоянного тока с печатным якорем через редуктор и шарико-винтовую пару.

Предметный стол, жестко связанный с ходовой гайкой, перемещается по роликовым направляющим станины вдоль оси Ох. Он приводится в движение двигателем постоянного тока. Вращение вала двигателя через муфту передается валу промежуточного редуктора, выходной вал которого через другую муфту вращает ходовой винт. Последний вместе с ходовой гайкой образуют шарико-винтовую пару, которая преобразует вращательное движение ходового винта в поступательное движение каретки-стола.

Механизмы передачи движения вдоль осей Оy и Оz аналогичны механизму перемещения предметного стола, Отличие заключается лишь в том, что выходной вал промежуточного редуктора образует одно целое с ходовым винтом, причем механизм вертикального перемещения имеет еще и разгрузочное устройство, которое компенсирует массу каретки с измерительной головкой,

Динамика и управление по каждой из координат не зависят от двух других. Это обстоятельство существенно упрощает синтез и анализ как программного, так и адаптивного управления КИР. Достаточно разработать метод и средства управления по одной координате, а использовать их можно и для управления по двум другим координатам. Исходя из этого, рассмотрим динамические свойства и возможности систем программного и адаптивного управления КИР УИМ-28 на примере управления столом-кареткой. С этой целью составим уравнение, описывающее динамику механизма перемещения стола-каретки вместе с измеряемой деталью. Обозначим через x линейное перемещение стола-каретки, а через φ, φ₁ и φ₂- углы поворота вала двигателя, ходового винта и вала редуктора соответственно. Эти переменные связаны между собой следующими уравнениями кинематики:

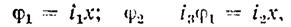(8.1)

где i₁, i₂, i₃ - передаточные отношения шарико-винтовой передачи, редуктора привода и промежуточного редуктора, причем i₁=2πh^-1, i₂=i₁i₂, h - шаг ходового винта.

С учетом трения и упругих деформаций в редукторе имеем

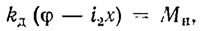(8.2)

где M_H - моменты нагрузки на валу двигателя; k_Д - коэффициенты упругих деформаций в приводе.

Динамика механизма перемещения стола-каретки описывается дифференциальным уравнением второго порядка

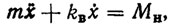(8.3)

где m - приведенная масса стола-каретки вместе с измеряемой деталью; k_B - коэффициент вязкого трения в исполнительном механизме.

Уравнение моментов на валу двигателя имеет вид

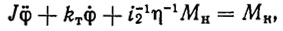(8.4)

где J - приведенный момент инерции двигателя; k_T - коэффициент трения; η - КПД редуктора; М_K - вращающий момент, определяемый формулой

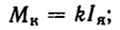(8.5)

k - параметр; I - сила тока в цепи якоря.

Уравнение электрических процессов в цепи якоря имеет вид

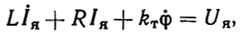(8.6)

где L и R - индуктивность и сопротивление в цепи якоря; U_я - напряжение в обмотке якоря. Управляющий сигнал (управление) и u пропорционально U_я. Точнее говоря, имеет место соотношение

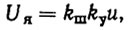(8.7)

где k_ш, k_у - коэффициенты усиления широтно-импульсного преобразователя (ШИП) и усилителя постоянного тока. Поскольку частота коммутации ШИП достаточно велика (около 15 кгц) и значительно больше частоты среза, то можно считать (по теореме Котельникова), что ШИП практически не влияет на динамические свойства системы перемещения стола-каретки.

Из анализа системы уравнений (8.1)-(8.7) следует, что текущее состояние КИР по координате x полностью определяется вектором

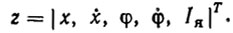(8.8)

Динамика КИР в терминах вектора состояний описывается следующей обобщенной математической моделью:

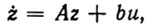(8.9)

где

(8.10)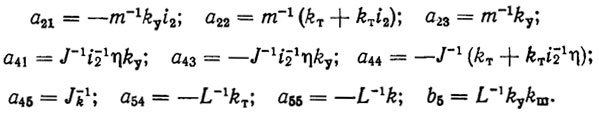

Остановимся на динамических свойствах модели (8.9). Эта модель линейна и вполне управляема, т. е. матрица управляемости S=||b,Ab,А²b, A³b, A⁴b|| не вырождена. Вследствие этого существует невырожденное линейное преобразование 1107]

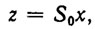(8.10)

приводящее уравнение (8.9) к каноническому виду

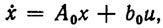(8.11)

где

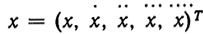
- вектор канонических переменных, а параметры a⁰₁, ...,a⁰₅. выражаются через параметры матрицы А и векторов b.

Разрешая уравнение (8.11) относительно управления, получим

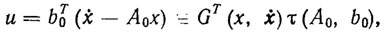(8.12)

где G и τ - некоторые вектор-функции 12. Структура этого уравнения подсказывает структуру регулятора, обеспечивающего асимптотическую устойчивость заданного ПД х_p(t). Тогда искомый закон управления (ЗУ) имеет вид [107]

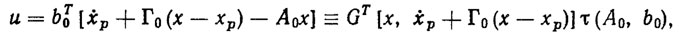(8.13)

где матрица коэффициентов усиления Γ₀ устойчива (гурвицева) и имеет каноническую структуру. Последнее означает, что

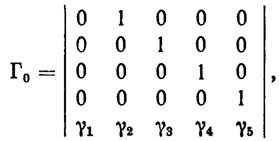(8.14)

причем вещественная часть собственных чисел λ _i(Γ₀), i= 1, ... ..., 5, матрицы Γ₀ отрицательная, т. е. корни уравнения det (λI - Γ₀)=0 лежат на комплексной плоскости слева от мнимой оси.

Выбором параметров γ₁...,γ₅ матрицы Γ₀ можно обеспечить не только асимптотическую устойчивость ПД х_p(t), но и экспоненциальный характер затухания переходных процессов. Это позволяет осуществлять автоматические измерения по программе без колебаний, избегая больших усилий на измерительный наконечник.

Для обоснования сформулированных свойств синтезированного регулятора подставим ЗУ (8.13) в уравнение динамики (8.9). Тогда получим следующее уравнение переходных процессов при перемещениях каретки-стола КИР:

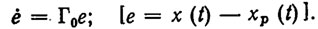(8.15)

Отсюда непосредственно следует, что переходные процессы в замкнутой системе (8.9), (8.13) затухают со следующей экспоненциальной оценкой:

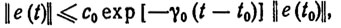(8.16)

где c₀,γ₀ - положительные параметры, зависящие только от выбора матрицы Γ₀, причем γ₀= -max Re λ_i

Регулятор в канонических переменных (8.13) замечателен тем, что для его реализации достаточно использовать только один прецизионный датчик - лазерный интерферометр (разрешающая способность 0,2 мкм), остальные компоненты вектора состояния легко вычислить с помощью формул численного дифференцирования. Однако, если измеряются все компоненты вектора z, то целесообразно синтезировать регулятор в физических переменных. Для этого нужно в формуле (8.13) сделать замену переменных и использовать сигналы обратной связи от соответствующих датчиков и преобразователей информации.

На практике зачастую не удается измерить все компоненты вектора состояний. Так, например, в КИР УИМ-28 непосредственно измеряются только переменные x, φ и I_я. Поэтому и регулятор здесь синтезируется как линейная комбинация указанных переменных, а также программной уставки x_p с коэффициентами усиления, настраиваемыми вручную.

Такой регулятор не обеспечивает асимптотической устойчивости программного движения каретки-стола, причем переходные процессы имеют колебательный характер. Неизбежные в процессе эксплуатации КИР возмущения и неопределенности (изменения массо-инерционных характеристик измеряемых деталей, дрейф коэффициентов трения и упругих деформаций) приводят к существенной потере точности наведения измерительной головки, уменьшению быстродействия, а в ряде случаев и к аварийным ситуациям (поломка наконечника измерительной головки и т. п.). В результате снижается точность измерений, производительность и надежность КИР.

Эти обстоятельства диктуют необходимость перехода к более, совершенным стабилизирующим регуляторам типа (8.13) и на их основе к адаптивным регуляторам [47, 107]. Последние одновременно осуществляют как сигнальную, так и параметрическую самонастройку стабилизирующего закона управления с целью обеспечения желаемого характера переходных процессов при всех возмущениях и не определенностях, возникающих в процессе эксплуатации КИР.

Рассмотрим методику расчета и проектирования адаптивных регуляторов применительно к задаче управления кареткой столом КИР У ИМ-28. Динамика объекта управления описывается дифференциальным уравнением (8.9), связывающим, с одной стороны, перемещение каретки х с вращающим моментом М_K на валу двигателя, а, с другой, - этот момент с управляющим напряжением u. Это уравнение зависит от ряда параметров (коэффициенты трения и упругих деформаций, электромеханические параметры привода и т. д.), многие из которых не только неизвестны, но и могут дрейфовать непредсказуемым образом в широком диапазоне. В этих условиях непосредственно воспользоваться формулой (8.13), описывающей идеальный стабилизирующий регулятор, нельзя, поскольку она зависит от неопределенных параметров. Представим формулу регулятора в виде

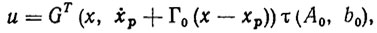(8.17)

где G, τ - некоторые заданные р-вектор-функции, определяемые соотношениями (8.16) и (8.17).

Идея адаптивного управления заключается в замене неизвестного вектора τ_*= τ (A₀, b₀) в аналитическом представлении идеального регулятора (8.17) его оценкой τ, которая формируется в процессе самонастройки согласно некоторому алгоритму, называемому алгоритмом адаптации. Для синтеза этого алгоритма можно воспользоваться методом адаптивного управления программным движением, описанным в гл. 3. Согласно этому методу алгоритм адаптации строится как алгоритм решения эстиматорных неравенств вида

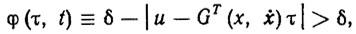(8.18)

где δ - Параметр, определяющий точности эстиматора (т. е. точность контроля за качеством отработки программного движения каретки). В качестве искомого алгоритма в принципе можно использовать любые рекуррентные и много шаговые алгоритмы решения неравенств вида (8.18), синтезированные в гл. 3.

В качестве примера приведем рекуррентный локально-оптимальный алгоритм адаптации градиентного (по отношению к эстиматорной функции φ) типа. Этот алгоритм определяется формулами:

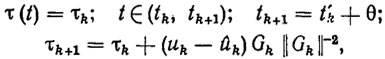(8.19)

где G_k=G[x(t'_k) ẋ_p(t'_k)]; û_k=G^T_kτ_k; u_k=G^T[x(t'_k), ẋ_p(t_k)+ Γ(x(t'_k)= x_p(t'_k))] параметр θ определяет время вычисления новой оценки τ_k+1 по старой τ_k т. е. характеризует быстро действие адаптатора.

Правильный выбор точности эстиматора δ быстродействия адаптатора θ и коэффициентов усиления регулятора Γ₀ позволяет реализовать заданное программное движение каретки КИР с любой наперед заданной точностью при любом уровне ограниченных параметрических возмущений. В этом заключается практическая ценность адаптивного программного управления КИР.

Важную роль при автоматизации измерений играют алгоритмы построения программных движений исполнительных механизмов КИР. Эффективным методом синтеза таких алгоритмов может служить метод параметрического синтеза и оптимизации, описанных в гл. 2. Проиллюстрируем преимущества этого метода на примере задачи автоматического перемещения каретки-стола из заданного начального состояния x₀ в желаемое конечное состояние x₁. Будем искать программное движение в виде

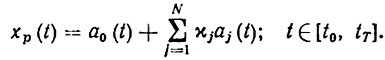(8.20)

В качестве -базисных функций можно взять функции:

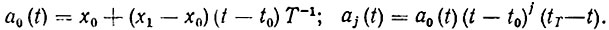(8.21)

Зная множества Q_x и Q _ẋ , определяющие конструктивные ограничения на x_p и ẋ _p задавшись функционалом качества J[x_p(·)], искомые параметры x₁, ...,x_N программного движения можно найти с помощью алгоритмов, описанных в гл. 2.

Рассмотрим простейший вариант задачи приведения каретки в заданное состояние x₁ за минимальное время. Пусть ограничения на x(t), ẋ(t) имеют вид

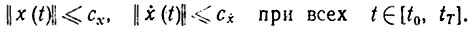(8.22)

Программное движение будем искать в виде

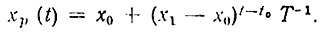(8.23)

Дифференцируя (8.23) и учитывая (8.22), получим

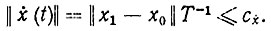(8.24)

Отсюда следует, что T≥c^-1_x||x₁-x₀||. Значит, оптимальное по быстродействию программное движение имеет вид

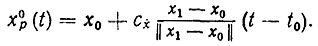(8.25)

Процесс автоматического программирования движения КИР в соответствии с описанными гибкими алгоритмами производится следующим образом. На первом (предварительном) этапе по чертежу детали определяется минимальное число точек, подлежащих измерению, и уточняются место и способ крепления детали, тип измерительного наконечника, форма протокола измерений и т. п. Измеряемые точки нумеруются на чертеже (в порядке наведения на них измерительного наконечника) и кодируются своими координатами (в системе координат детали). На втором этапе по этим данным строится в аналитическом виде программное движение исполнительных механизмов КИР. При этом центр измерительного наконечника наводится на выбранную точку детали, заданную своими координатами. В момент соприкосновения наконечника с деталью происходит автоматическое считывание измеряемых координат.

Цифровое моделирование и реализация синтезированного адаптивного управления ПД в канонических координатах требуют формирования производных до пятого порядка от программного и реального перемещения каретки х_p(t),x (t). Учитывая высокую точность датчиков положения (0,2 мкм), эти производные можно формировать численно. При этом отпадает необходимость в сложных и ненадежных каналах обратной связи через сигналы тахогенератора и ток якоря, используемых в системе сервоуправления КИР УИМ-28. В общем случае для восстановления канонического вектора состояний x(t) по сигналам от датчиков можно воспользоваться теорией и известными схемами наблюдателей [19, 31, 58], обеспечивающими асимптотическую идентификацию вектор а состояний.