8.6. Мультимикропроцессорная реализация и моделирование адаптивного управления измерительным роботом

Рассмотрим проектирование мультимикропроцессорной системы для реализации адаптивного управления КИР типа УИМ-28. В качестве базовой структурно-функциональной схемы такой системы можно взять схему, описанную в п. 3.10 и представленную на рис. 3.4. Для организации параллельно-последовательных вычислений в соответствии с этой схемой на i-м такте цифрового адаптивного управления производятся следующие операции:

1. формирование ПД х_p(t_i) и его производной ẋ_p(t_i);
2. синтез управляющего воздействия u(t_i);
3. оценка качества управления с помощью эстиматорной функции φ(τ_k, t_k);
4. вычисление новой оценки параметров τ_k+1.

Все указанные операции должны осуществляться в реальном масштабе времени. Это обстоятельство определяет требования к реализующим их программатору, регулятору, эстиматору и адаитатору. При этом вычисление программы измерений программатором (расчет и оптимизация коэффициентов x_j в параметрическом представлении ПД) и автоматическая регулировка качества переходных процессов (расчет коэффициентов усиления Γ₀ в каналах обратной связи и точности δ решения эстиматорных неравенств) могут, осуществляться на микроЭВМ типа "Электроника-60" до начала управления. Функции регулятора, эстиматора и адаптатора естественно возложить на запрограммированные соответствующим образом микропроцессоры.

Благодаря такому алгоритмическому распараллеливанию оказывается возможным не только произвести заранее необходимые трудоемкие расчеты, но и распараллелить процессы адаптации и собственно управления. Следует отметить, что возможно дальнейшее распараллеливание вычислений при реализации отдельных алгоритмов, основанное на использовании параллельных сумматоров, параллельных умножителей и т. д.

Для реализации описанной мультимикропроцессорной системы можно использовать серийно выпускаемые микропроцессоры. С учетом высоких требований к быстродействию системы адаптивного управления (и, особенно, к адаптивному), а также необходимость изменения разрядности при автоматической регулировке точности были выбраны микропроцессоры серии К-580 с использованием буферного запоминающего устройства (БЗУ) на микросхемах К589ИР12 и К155ТМ7 для организации обмена между модулями и арифметического расширителя (БАР) на серийно выпускаемых микросхемах К155ИПЗ.

Микропроцессорная система адаптивного управления включает следующие блоки: блок идентификации состояний ЭМР (БИС), блок формирования управляющего воздействия (БФУВ), блок проверки качества управления (БПКУ), блок адаптации (БА). Каждый из этих блоков представляет собой микропроцессор и оперативное запоминающее устройство типа К565РУ2А, полупостоянное запоминающее устройство типа К558РР1, БЗУ и БАР указанных типов, а также цифроаналоговые и аналого-цифровые преобразователи. Число этих блоков зависит от числа степеней свободы m исполнительного механизма КИР и сложности алгоритмов адаптивного управления.

Другой вариант мультимикропроцессорной реализации адаптивного управления УИМ-28 основывается на использовании микропроцессорного набора серии К-589. В состав этого набора входят блок управления памятью, один-два модуля ПЗУ, 2-разрядные наращиваемые модули арифметико-логического устройства (АЛУ), четыре-пять регистров. Быстродействие АЛУ в конвейерном режиме составляет 0,1 мкс на микрокоманду, сложение модулей 32-разрядных чисел в ПЗУ выполняется за 0,1 мкс, умножение - за 2 мкс. Как показывают расчеты [47], для вычисления одного такта цифрового адаптивного управления КИР за время, не превышающее 256 мкс. требуется восемь микропроцессоров типа К-589. Такое быстродействие мультимикропроцессорной системы адаптивного управления позволяет не только полностью автоматизировать процесс наведения ИГ, по и гарантировать высокое качество переходных процессоров в условиях значительной неопределенности и непредсказуемого дрейфа параметров КИР и измеряемой детали.

В заключение опишем экспериментальные результаты моделирования на ЭВМ не адаптивного и адаптивного управления КИР типа УИМ-28. Ввиду того что коэффициент при старшей производной весьма мал, порядок уравнения динамики (8.11) понижается до четвертого. Соответственно упрощаются и законы не адаптивного и адаптивного управления.

Рассмотрим сначала режим стабилизации ПД. Были проведены две серии экспериментов, в которых программный закон перемещения каретки формировался по формуле

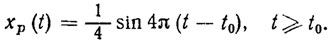
В первой серии исследовалось влияние начальных и параметрических возмущений на качество не адаптивного стабилизирующего управления КИР. Управление формировалось по формуле (8.13), где вместо неизвестных параметров использовались некоторые их оценки, а в качестве матрицы коэффициентов усиления Γ₀ была взята устойчивая (4*4) матрица канонического вида с собственными числами: λ₁= -11, λ₂= -12, λ₃= -13, λ₄=-14. Длина такта управления и шаг интегрирования уравнений динамики равнялись 0,005 с.

В идеальных условиях, когда все параметры, входящие в закон управления (8.13), известны, переходные процессы имеют экспоненциальный характер. Этим обеспечивается точное и быстрое отслеживание ПД. В действительности ряд параметров КИР неизвестен, причем некоторые из них изменяются в широком диапазоне. Прежде всего это относится к массо-инерционным характеристикам измеряемой детали, силам трения, коэффициентам упругих деформаций в редукторе, электрическим параметрам двигателей. В результате возникают параметрические возмущения, величина || τ_* - τ₀|| которых варьировалась в различных экспериментах в пределах от 5,25*10^-2 до 5,25.

Характер переходных процессов в замкнутом КИР в типичном эксперименте изображен в канонических и физических координатах на рис. 8.13, а, б штриховой линией. Как видно из этого рисунка, даже небольшие параметрические возмущения (рис. 8ЛЗ, в) могут приводить при не адаптивном управлении к существенной потере точности при отработке ПД (около 10^-2 м) и к колебаниям измерительного наконечника вблизи траектории, определяемой ПД.

В этих же условиях во второй серии экспериментов моделировалось адаптивное управление (8.17)-(8.19). Оно фактически обеспечивает осуществление ПД с наперед заданной точностью (около 10^-7 м). Это видно из того же рис. 8.13, а, б, где переходные процессы в КИР с адаптивным управлением выделены сплошной линией.

В качестве алгоритма адаптации (АА) в этом эксперименте использовался рекуррентный локально-оптимальный алгоритм вида (8.19). Отвечающий ему процесс адаптации иллюстрируется рис. 8.13, в, откуда видно, что время адаптации составляет примерно 0,8 с, причем оценка τ (t) лишь приближается к неизвестному τ_*, но фактически его не идентифицирует. Использование в качестве АА много шагового оптимального алгоритма, описанного в п. 3.7, обеспечило практически точную идентификацию вектора параметров τ_*, причем время адаптации уменьшилось и составило 0,07 с.

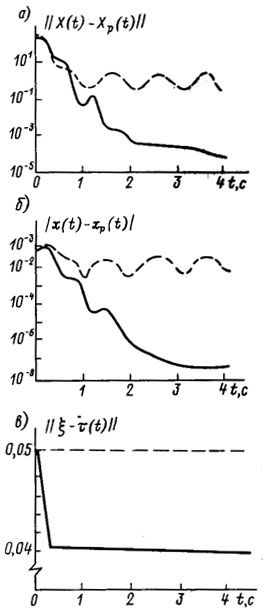
Рис. 8.13. Адаптивная стабилизация программных движений КИР

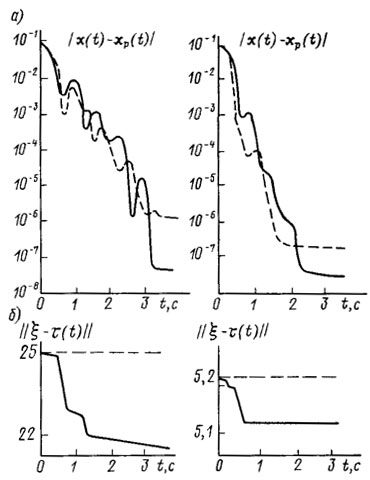
Рис. 8.14. Адаптивное Самонаведение измерительной головки КИР

Рассмотрим теперь экспериментальные результаты по адаптивному самонаведению наконечника ИГ. В описываемых экспериментах закон управления также формировался по формуле (8.13) или (8.17). Однако ПД строилось иначе: в качестве x_p(t) бралось требуемое состояние измерительного наконечника. Обычно это состояние таково: x_p(t)=(x_{1, 0, 0,0)^T}, т. е. наконечник должен занять положение с нулевыми скоростью и ускорением. Программное положение x₁ измерительного наконечника определялось исходя из чертежа аттестуемой детали.

В первой серии экспериментов исследовалось влияние параметрических возмущений на процесс самонаведения щупа по формуле (8.13), где в качестве неизвестного вектора параметров τ_* использовалась некоторая его оценка τ₀. Переходные процессы для различных уровней параметрических возмущений (около 24,8 и 5,19), характеризующих априорную неопределенность, изображены на рис. 8.14 штриховой линией. Сравнительно низкая точность наведения измерительного наконечника в этих экспериментах является следствием априорной неопределенности параметров КИР, которая в процессе самонаведения не уменьшается, так как в данном законе самонаведения не предусмотрена адаптация.

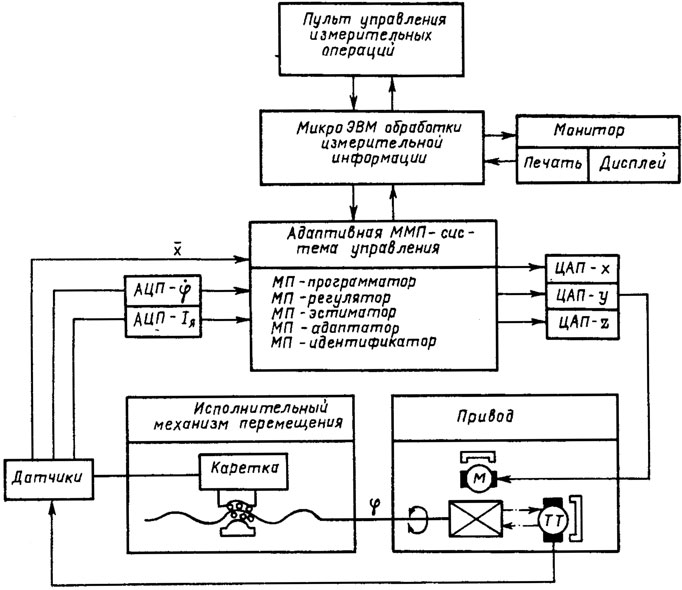
Рис. 8.15. Структурно-функциональная схема мультимикропроцессориой системы адаптивного управления трех координатным измерительным роботом

Во второй серии экспериментов моделировалось адаптивное самонаведение ИГ в соответствии с формулами (8.17)-(8.19) при различном уровне параметрических возмущений. В этом случае благодаря адаптивной подстройке параметров закона самонаведения (8.17) в силу АА (8.19) точность приведения измерительного наконечника в требуемое состояние достигала заданной величины (около 10^-7 м). Это видно из рис. 8.14, а, где переходные процессы самонаведения при различном уровне возмущений (около 25 и 5,2) изображены сплошными линиями. На графиках рис. 8.14, б представлены процессы адаптации в силу рекуррентного АА вида (8.19). Этот АА не приводит к точной идентификации неизвестного вектора τ_*. Тем не менее именно АА (8.19) в сочетании с законом самонаведения (8.17) обеспечивает требуемую точность наведения наконечника ИГ в контрольные точки. Отметим, что использование в качестве АА оптимального много шагового алгоритма, описанного в п. 3.7, приводит к практически мгновенной идентификации (время адаптации составляет 0,05 с) и к точному приведению измерительного наконечника в заданную контрольную точку.

Структурно-функциональная схема КИР с адаптивным управлением представлена на рис. 8.15. Неотъемлемой частью мультимикропроцессорной системы управления этого КИР является описанное выше алгоритмическое и программное обеспечение.

На основании полученных теоретических и экспериментальных результатов можно сделать общий вывод о том, что переход к адаптивному управлению КИР и использование микропроцессоров и микроЭВМ для его реализации позволяют полностью автоматизировать как процесс формирования программы измерений, так и процесс ее отработки в нестационарных и неопределенных условиях. При этом достигается высокое качество управления (точность и производительность КИР приближаются к предельно возможным величинам), увеличивается гибкость и надежность КИР, что особенно важно в условиях ГАП.