8. Системы управления роботов

8.1. Задачи, решаемые системой управления робота

Пусть изображенный на рис. 8.1 подвижный манипуляционный робот с бортовой системой управления (СУ) должен переместиться из некоторого начального положения в рабочую зону и взять в ней предмет Ц. Для простоты вначале положим, что робот должен двигаться вдоль координаты из некоторого начального положения, характеризуемого значениями координат х_н, y_н центра тяжести тележки и значениями углов α_н, β_н манипулятора, в некоторое конечное положение x_к, y_к, α_к, β_к.

Если ввести обобщенные координаты q_i так, чтобы выполнялись соответствия: х → q₁; y → q₂; α → q₃; β → q₄, то начальное положение робота можно охарактеризовать вектором Q_H = [q_1н, q_2н, q_3н, q_4н], конечному положению будет соответствовать вектор Q_K = [q_1к, q_2к, q_3к, q_4к], а для любого j-го промежуточного положения будем иметь

Подобно этому для манипулятора с n степенями подвижности получим

Причем переход из Q_H в Q_K можно представить в виде некоторой последовательности переходных положений

которые в непрерывном времени t образуют траекторию перемещения манипулятора Q(t).

Очевидно, что для перевода робота из Q_H в Q_K к его звеньям необходимо приложить соответствующую последовательность управляющих воздействий {U_j}. Причем для перевода робота из состояния Q_j в состояние Q_j+1 нужен управляющий вектор

компоненты которого представляют собой сигналы, подаваемые на приводы соответствующих звеньев манипулятора или устройств перемещения. Иными словами, зная Q(t) необходимо определить соответствующий закон изменения U(t), который и позволит реализовать переход схвата из точки x_cн, y_сн в точку х_ск, y_ск (см. рис. 8.1), поскольку в общем случае справедливо соотношение

где S = [х_с, y_с, z_c] - вектор, определяющий положение центра схвата в трехмерной рабочей зоне (0, х, y, z).

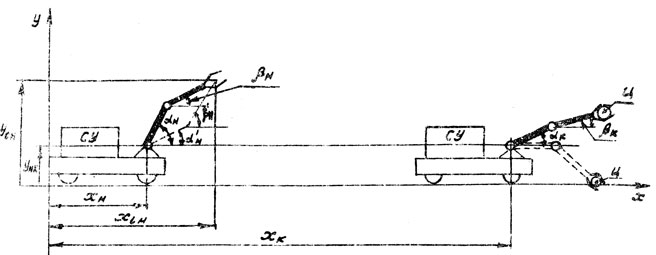
Рис. 8.1

Это так называемая прямая кинематическая задача, позволяющая по значениям обобщенных координат находить координаты схвата в рабочем пространстве робота.

Однако в тех случаях, когда удобно задавать не Q, а желаемые значения вектора S, необходимо решать обратную кинематическую задачу

Неудобным при этом является то, что функции F и F^-1 неоднозначны. Например, из рис. 8.1 видно, что вектору S_H = [x_сн, y_сн] соответствуют два (если манипулятор - плоский двухзвенник) вектора, а именно тот, который определяется значениями углов α_н, β_н и тот, который определяется значениями α'_н и β'_н. При большем числе степеней подвижности неоднозначность увеличивается, что и позволяет многостепенному манипулятору обходить препятствия.

Итак, когда задается траектория схвата S(t), система управления должна вначале рассчитать траекторию Q(t) из соотношения

и после этого определить закон изменения управляющего вектора U(t). Определение и отработка U(t) должны вестись с учетом динамических свойств робота.

Все это весьма непростые задачи. Их решение существенно усложняется, если в процессе реализации траектории Q(t) в рабочей зоне возникают препятствия. Ясно, что препятствия нужно обходить и оптимизировать при этом траекторию движения манипулятора.

В простейших случаях траекторию Q(t) задает либо предварительно формирует сам оператор. В более сложных случаях, например в случае роботов с элементами искусственного интеллекта, эта траектория формируется автоматически в процессе работы робота.