3.4. Формальные грамматики

Уже было сказано, что для описания языка-объекта должен быть известен метаязык. В качестве самого первого метаязыка мы вынуждены применить естественный (в данном случае - русский) язык. В предыдущем примере мы так и сделали. Сейчас мы воспользуемся русским языком для того, чтобы описать несложный и удобный метаязык, пригодный для описания синтаксисов многих формальных (но, конечно, не всех) языков.

Условимся, что в формальных языках, для описания которых будет использован создаваемый нами метаязык, никогда не будут применяться символы "<", ">", ":: =" и "|". Первые два назовем угловыми скобками (соответственно открывающей и закрывающей). Текст на естественном языке, заключенный в угловых скобках, будем считать метасимволом (т. е. одной буквой, применяемой для описания языка-объекта). Это означает, что в данном применении такой текст нельзя разлагать на части или вносить в него какие-либо изменения. Символ ":: =" будем считать условной записью фразы "по определению есть", а символ "|" - обозначением слова "или".

Формальную грамматику запишем в виде последовательности так называемых метаформул. Каждая метаформула начинается с метасимвола (содержащего угловые скобки), после которого стоит знак ":: =", а затем записана правая часть формулы, состоящая из одного фрагмента или нескольких фрагментов, разделенных знаками "|". Фрагмент может быть пустым (в этом случае ничего не пишут), состоять из одного слова (в частности, однобуквенного) или представлять собой последовательность слов, записанных без знаков раздела. В последнем случае фрагмент обозначает результат последовательно (считая слева направо) выполненных операций сцепления слов. Каждая метаформула определяет стоящий в ее начале метасимвол, как групповое обозначение любых конструкций, указанных в ее правой части. Если метасимвол присутствует несколько раз в одном или нескольких фрагментах правой части, его экземпляры считаются между собой независимыми, так что правая часть формулы обозначает множество конструкций со всеми возможными значениями этого метасимвола.

Так как в метаформулах никак не указаны их границы, а применение обычных знаков препинания приводит к смешению описываемого языка с русским, который при этом является мета-метаязыком, то условимся каждую метаформулу начинать с абзаца, после ее конца не ставить никаких знаков препинания и следующий за ней текст начинать только с абзаца. В случае необходимости перехода из строки в строку никаких знаков переноса ставить не будем.

Рассмотренный метаязык известен под названием нотации Бекуса или Бекуса-Наура. Опишем с его помощью уже знакомую нам грамматику арифметического языка.

Покажем, как с помощью этой грамматики получается уже знакомая нам формула ¬(((а)') = (0)). В силу первого фрагмента первой метаформулы а есть <переменная>; в силу второго фрагмента второй метаформулы а есть <терм >; в силу третьего фрагмента той же второй метаформулы (а) - тоже <терм>. В силу первого фрагмента второй метаформулы 0 тоже <терм >. С помощью первого фрагмента третьей метаформулы получаем, что ((а)') = (0) есть <формула>, а с помощью последнего фрагмента третьей метаформулы узнаем, что ¬(((а)') = (0)) - тоже <формула>.

Остается подвести итог наших рассуждений. Говоря о формальном языке, мы всегда будем иметь в виду, что существует некоторое множество L символьных конструкций определенного класса (А, В, ∑), называемых предложениями и построенных с помощью конечной системы однозначных правил, называемых синтаксическими. Если это так, то кроме того существует некоторое множество S (об элементах которого не делается никаких предположений) и задана конечная система правил, называемых семантическими, с помощью которых каждому предложению, принадлежащему L, ставится в соответствие один единственный (или не ставится ни один) элемент из S.

Множество L называется формальным языком. Совокупность множеств L, S и отображения, порождаемого семантическими правилами, называется формальным языком, наделенным (формальной) семантикой.

Совокупность описания (А, В, ∑) класса символьных конструкций и системы синтаксических правил называется формальной грамматикой.

Мы не требуем, чтобы предложения языка были обязательно словами или последовательностями слов. Они могут быть конструкциями любого вида. Мы не требуем также, чтобы синтаксические правила обязательно каким-либо способом "складывали" конструкции из исходящих морфем, как в естественных языках. Синтаксическое правило может предписывать выполнение любого преобразования.

С помощью семантических правил можно понимать предложения формального языка. А вот "говорить" на нем они нам не помогут. Для этого необходимы другие правила, которые определяют преобразование элементов множества S в символьные конструкции, принадлежащие L, причем определяемое ими преобразование должно быть обратным преобразованию, определяемому семантическими правилами. При разговоре двух людей на естественном языке множество S представляет собой совокупность образов и понятий, каким-то способом зафиксированных как в мозгу одного, так и в мозгу другого собеседника. Один из них как-то отображает один из образов или "мысль" на соотвествующее предложение естественного языка. Он говорит. Другой, слыша предложение, каким-то способом производит его отображение на зафиксированный или на составленный в мозгу экземпляр того же образа или той же "мысли". Он понимает. Вот грубая модель применения естественного языка. Как осуществляются прямое (когда говорят) и обратное (когда понимают) отображение, мы можем только предполагать. Этими вопросами занимаются физиология, психология и, вероятно, еще другие науки. Обычно, поняв предложение, человек как-то перерабатывает содержащуюся в нем информацию. При пользовании формальным языком переработка поступившего предложения может быть произведена и без этапа "понимания".

По отношению к формальному языку "говорение" мы будем называть генерацией предложения, а восприятие предложения, независимо от того, происходит ли его "понимание" или оно поступает в переработку - его рецепцией.

В роботах мы найдем и генерацию и рецепцию предложений формального языка (а иногда и нескольких).

Теорию формальных языков, приспособленную к потребностям робототехники, мы будем называть кибернетической лингвистикой. Некоторые ее проблемы играют большую роль в области применения ЭВМ и программирования, что вполне естественно.

Нотация Бекуса позволяет описывать формальные грамматики языков, предложения которых являются словами, да и то не любые. Действительно, рассмотрим весьма простой язык, для которого

а вот предложение языка пусть получается путем сцепления двух одинаковых фраз. С помощью нотации Бекуса задать такой способ построения предложений нельзя потому, что метаформула

кроме допустимых предложений, определяет как предложения и недопустимые слова.

Тем не менее, нотация Бекуса играет и в практике и в теории значительную роль. Заметим, что если бы мы расширили набор операций, которые применяются для конструирования предложений, т. е. обобщили нотацию Бекуса, то смогли бы построить грамматику и такого языка, о котором было сказано выше. Например, введем операцию удвоения, которую будем обозначать двойкой, поставленной справа и выше закрывающей угловой скобки. При этом необходимо, чтоб такая "подпрыгнувшая" двойка не была буквой языка-объекта. В этом случае стала бы возможной метаформула

Обобщить рассмотренный способ формального описания грамматик формальных языков можно следующим образом. Пусть х₁, х₂, ..., х_k метасимволы, являющиеся именами исходных символьных конструкций, называемых морфемами. Пусть, кроме того, х_k+1, х_k+2, ..., x_n, x* - метасимволы, являющиеся именами результатов операций над символьными конструкциями. Из этих метасимволов х* выделен, как обозначающий предложение языка-объекта. Далее, пусть метасимволы φ₁, φ₂, ..., φ_m означают операции над конструкциями. Формальная грамматика принимает вид совокупности описания класса конструкций (A, В, ∑), которому принадлежат предложения языка-объекта, конечного множества морфем, снабженных именами х₁, х₂, ..., х_k и конечного набора метаформул вида

где r - ранг операции φ_V. Среди метаформул одна или несколько должны в левой части иметь х*.

Синтаксис принимает вид набора метаформул.

Построение предложений языка-объекта с помощью формальной грамматики называется порождением предложения. Оно заключается в последовательном выполнении метаформул (в любом возможном порядке и с любым числом применений каждой из них), причем последняя из выполненных должна в левой части содержать х*. В качестве операнда может быть взято любое значение метасимвола, являющегося аргументом правой части мета-формулы.

Интересный частный случай. Всякое конечное множество символьных конструкций является формальным языком.

В этом легко убедиться, приняв заданные символьные конструкции за морфемы и считая, что в левых частях всех метаформул стоит JC* И все операции, указанные в них, являются одноместными тождественными. Синтаксис при этом примет вид: х*:: = x_i, i = 1, 2, ..., k.

Формальная грамматика с математической точки зрения является конечным (или, как говорят, финитным) описанием множества символьных конструкций, которое, в принципе, может быть и бесконечным.

В практике приходится иметь дело с символьными конструкциями, фиксированными в запоминающих устройствах, объемы которых конечны, а значит, и количества допустимых символьных конструкций оказываются конечными, так что практически применяются либо конечные формальные языки, либо их конечные подъязыки. Тем не менее, применяемые формальные грамматики редко бывают столь простыми, как в указанном случае.

Теория формальных языков для нас настолько важна, что целесообразно привести еще две иллюстрации.

Пример 3.1. Общеизвестная десятичная система счисления представляет собой формальный язык. Покажем это, построив ее формальную грамматику. Ограничимся случаем целых неотрицательных чисел (только ради экономии места и времени). Морфемами десятичной системы счисления являются однобуквенные слова, составленные из букв в алфавите 0123456789. Запишем это в виде метаформулы

Предложениями языка являются так называемые "записи чисел", определяемые следующей метаформулой:

Первый фрагмент этой метаформулы определяет, что запись числа может состоять из одной цифры. Второй фрагмент говорит, что если к записи числа приписать какую-нибудь цифру, то опять получится запись числа. Так, 5, 59, 592 - это все записи чисел.

Пример 3.2. Предположим, что формальная грамматика из примера 3.1 является только частью интересующей нас более сложной грамматики, содержащей еще метаформулу

Пусть при этом st (x, y) означает операцию подписывания y под x (при этом неявно используется связь вертикального следования y за x). В силу первого фрагмента последней формулы "02015" можно считать столбцом. В силу ее второго фрагмента столбцами будут также ' 02015 02015

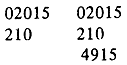
и т. д.

Зарегистрируйтесь на сайте https://velikielukism.com и насладитесь времяпровождением с красивой и интеллигентной девушкой.