2. Уравнения механических цепей

Рассмотрим схему манипулятора, изображенную на рис. 7. Его приводы осуществляют качание плечевого и кистевого суставов в плоскости; α₁, α₂, α₃ - углы поворота звеньев, l_i - длина i-го звена, m_i - сосредоточенная масса звена, r_i - расстояние центра тяжести звена (точки, в которой сосредоточена масса) от его оси вращения. В величине массы m_i третьего звена учитывается масса переносимого груза.

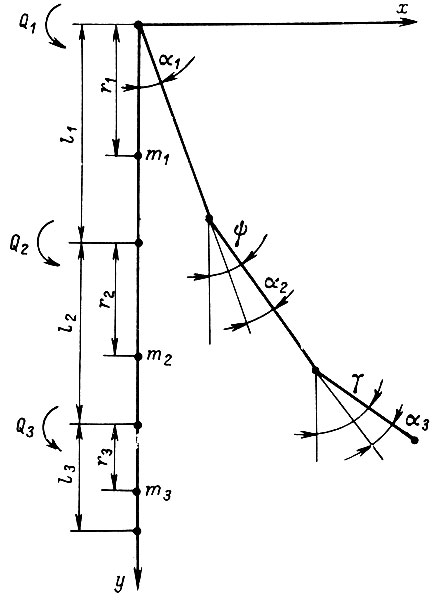
Рис. 7

В дальнейшем будем разделять движения на основные, т. е. не учитывающие волновые колебания звеньев из-за нежесткости конструкции, и дополнительные - упругие волновые колебания изгиба. Раздельное исследование этих движений практически допустимо при низкочастотных переходных процессах в манипуляторе. Воспользуемся уравнением Лагранжа для основных движений

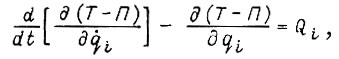
где Т и П - кинетическая и потенциальная энергия механической системы; 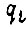- обобщенная координата о учетом статических изгибов звеньев; для схемы на рис. 7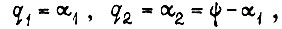 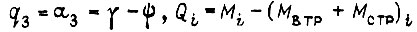- обобщенный момент неконсервативной силы; M_i - момент, развиваемый приводом на левом конце своего звена, M_втр и M_стр - моменты сил вязкого и сухого трений; t - время.

Кинетическая энергия системы

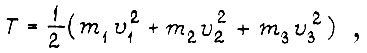
где v_i - скорость перемещения центра тяжести i-го звена. Для схемы на рис.7

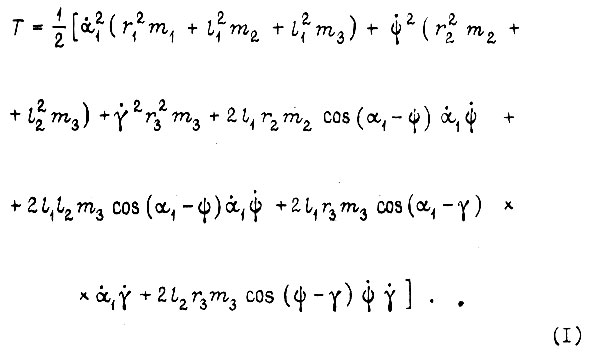
Потенциальная энергия системы

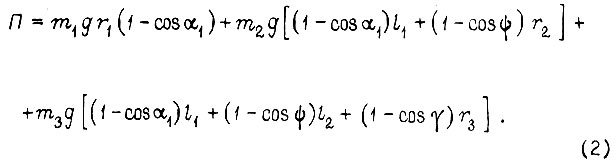
Формулы моментов сил Q₁, Q₂, Q₃ из уравнения Лагранжа:

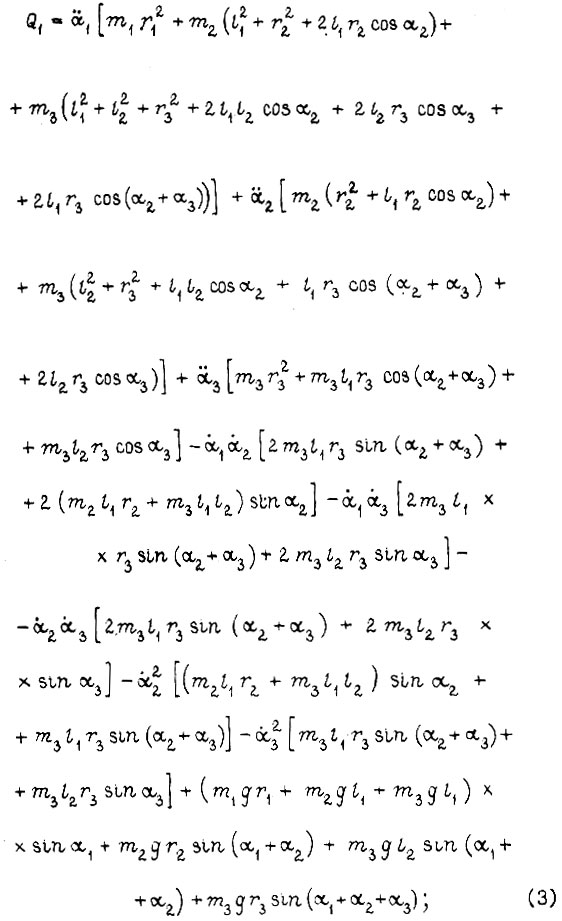
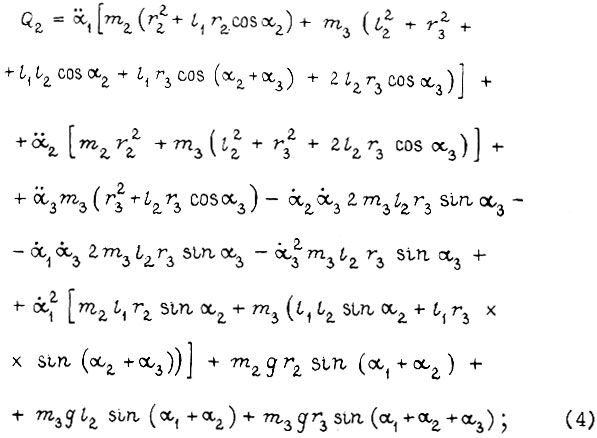
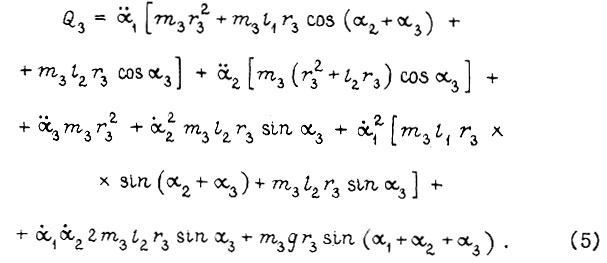
Учитывая, что вращающий момент M_i для i-й степени свободы (см. рис. 7) есть

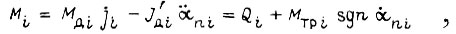
где M_дi - момент, развиваемый двигателем; J'_дi - момент инерции двигателя, приведенный к шарниру; j_i - передаточное число от двигателя к шарниру; M_трi sgn α_ni - момент сухого трения (М_стр)_i; α_ni - угол поворота вала привода, представим (3), (4), (5) в виде

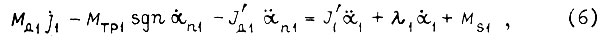
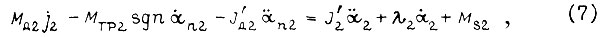
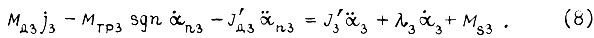
Здесь

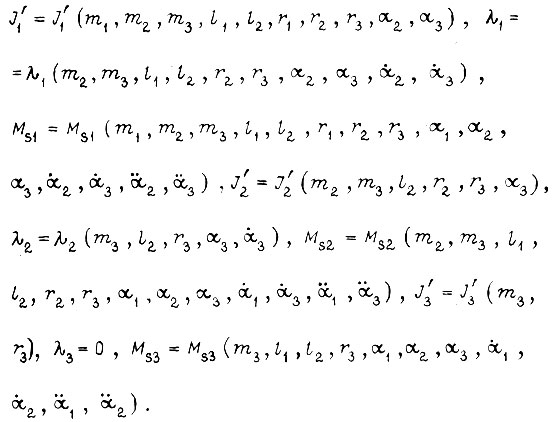
В формулах (6), (7), (8) вязкое трение не учитывается.

Допустим, что механическая характеристика 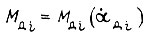системы силовой электронный преобразователь - двигатель является линейной. Тогда

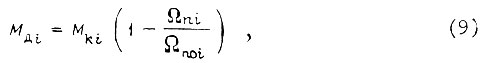
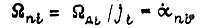где - момент короткого замыкания двигателя - угловая скорость вращения вала в шарнире; 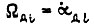- угловая скорость вала двигателя; 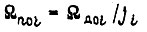- скорость идеального холостого хода; 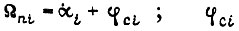- угол поворота свободного конца i-го звена робота по отношению к концу, соединенному с приводом, в результате изгиба звена. После подстановки (9) в (6), (7), (8) получаем систему дифференциальных уравнений, описывающих движение приводов манипулятора, изображенного на рис. 7:

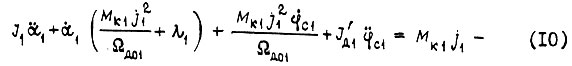
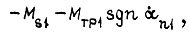
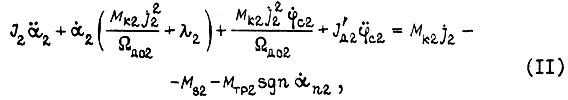
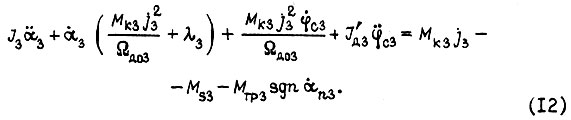
Здесь Скорость Ω_д0i и момент зависят от величины сигнала управления, поступившего к силовому преобразователю, и от вида обратной связи, охватывающей преобразователь и двигатель и формирующей механическую характеристику привода. В уравнениях (10), (11), (12) не учтена инерционность электрических силовых цепей.

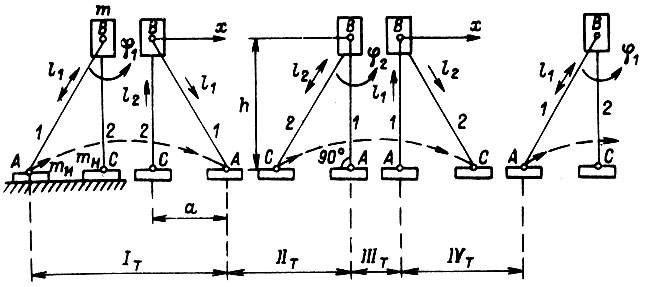
Рис. 8

На рис. 8 изображен двуногий шагающий механизм: m - масса, перемещаемая горизонтально в вертикальной плоскости; инерцией ног 1, 2 пренебрегаем; m_н - массы, на которые опираются ноги в шарнирах А, C .С помощью приводов можно изменять длину каждой ноги и производить поворот ног в плоскости рисунка вокруг оси В. Периодическое движение механизма в направлении x складывается из четырех тактов. В первом такте происходит поворот ноги 1 вокруг оси В с одновременным укорочением, а затем удлинением. Во втором такте происходят приращения длин ног 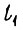, , 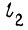в третьем - поворот ноги 2 и приращение 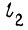, в четвертом в результате изменения длин ног механизм приходит к исходному состоянию. По аналогии с (10), (II), (12) запишем уравнения динамики приводов:

в первом такте

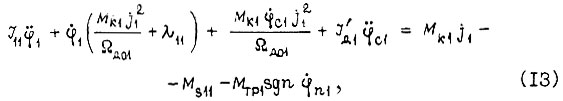
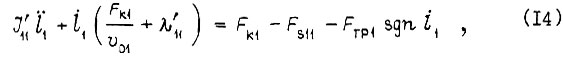
во втором такте

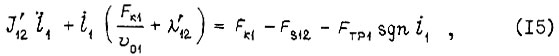
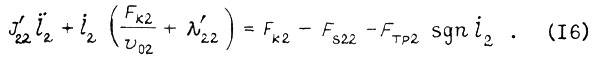
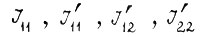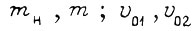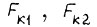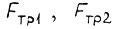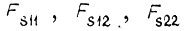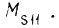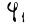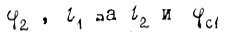Здесь в коэффициентах учитываются массы - скорости идеального холостого хода линейных двигателей; - силы короткого замыкания этих двигателей; - силы трения; силы аналогичны моменту В третьем такте справедливы уравнения (13), (14), если заменить на на 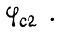Для четвертого такта в уравнениях (15), (16) меняем местам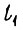и и 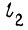. Суммарное изменение 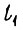в первом такте либо 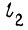в третьем равно нулю, при этом суммарный угол поворота ноги равен 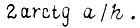Для второго такта из уравнения связи 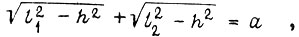, где 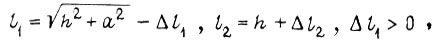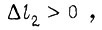получаем 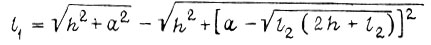Текущее перемещение x массы m равно 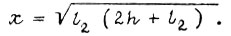Суммарные абсолютные приращения 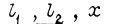за второй либо четвертый такт 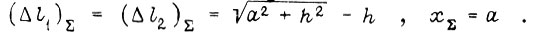Полное перемещение массы m в направлении x за период движения механизма равно 2a.

Исследуем дополнительные изменения положений звеньев рабочего органа, представляющие собой волновые упругие колебания изгиба. Запишем уравнение колебаний звена манипулятора как однородной балки

где μ - масса балки, приходящаяся на единицу ее длины; ε = const при постоянном поперечном сечении звена; x - координата, отсчитываемая вдоль неизогнутой балки от левого конца вправо; y - отклонение перпендикулярно к оси x.

В этом уравнении не учитывается деформация статического изгиба. Предположим, что оно описывает установившиеся колебания с частотой ω, т. е.

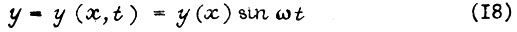
Тогда (17) принимает вид

Приходим к общему решению

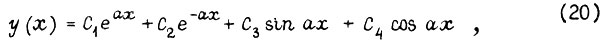
где

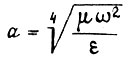
Для левого конца балки, связанного с выходным валом привода, принимаем как для опертого конца 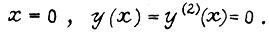Это дает два условия для определения постоянных 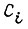в решении (20): 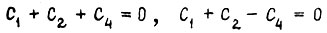, откуда 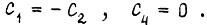Получаем из решения (20) формулу y(x):

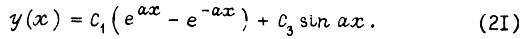
Для правого конца 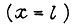, являющегося свободным, принимаем 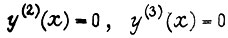(равны нулю изгибающий момент и перерезывающая сила). Имеем еще два условия для определения коэффициентов в формуле y (x):

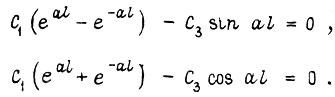
Отсюда получаем, что либо 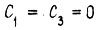, и в этом случае отсутствует любой прогиб, либо справедливо соотношение

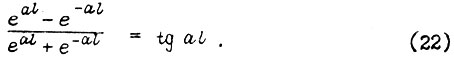
Графическое решение (22) дает множество значений коэффициента а и соответственно множество возможных значений частоты 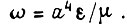Коэффициенты 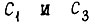определяем из следующих соображений.

Во-первых, наибольшая потенциальная энергия балки, которую она имеет в процессе колебаний:

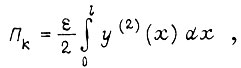
равна кинетической энергии при максимальных линейных скоростях ее всех точек:

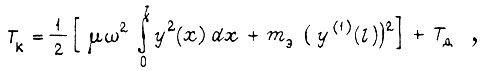
где 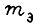- эквивалентная масса остальных звеньев, переносимых данным звеном, сосредоточенная на правом конце; 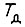- энергия, отдаваемая приводу. Тогда

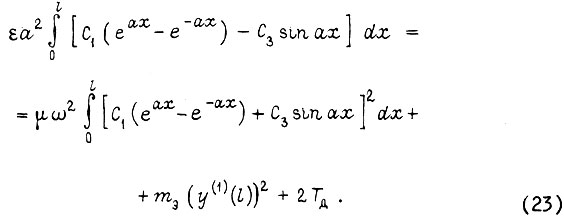
Во-вторых, энергия, поддерживающая процесс генерации колебаний изгиба, в каждый момент времени определяется всеми предыдущими приращениями угла изгиба звена 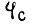Введем в рассмотрение величину

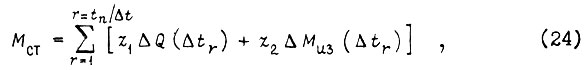
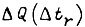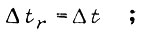
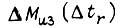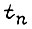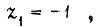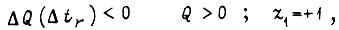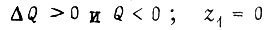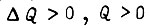где - приращение обобщенной силы для данного привода (по уравнению Лагранжа) на малом отрезке времени - приращение изгибающего момента от собственного веса звена; - время переходного процесса; если , если при или 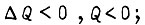аналогичные значения принимает 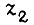по отношению к полярности 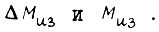Момент определяем по формуле

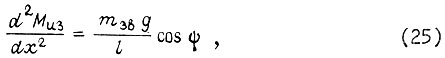
где 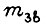- собственная масса звена; g - ускорение свободного падения; φ - угол между вертикалью и направлением, перпендикулярным к неизогнутой линии звена x. Решив уравнение (25), подставляем x = l - длину звена. Угол изгиба 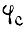есть

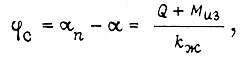
где 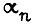- угол поворота вала привода (после редуктора); α - угол поворота свободного конца звена; 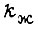- коэффициент жесткости звена на изгиб.

Наличие 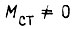есть причина появления волновых колебаний. Потенциальная энергия, соответствующая 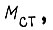равна 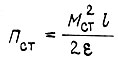(максимально возможная энергия). Последнее условие для определения c₁ и c₃

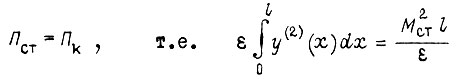
или

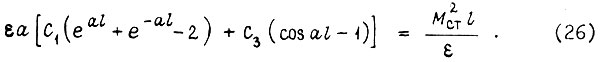
Поскольку правая часть (26) зависит от времени в соответствии c (3), (4), (5), (24), (25), то 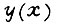есть функция, определяемая по формуле (21), где 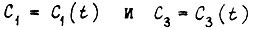в данном переходном процессе манипулятора. Наибольшее значение y можно определить, перебирая значения ω, удовлетворяющие (22). Заметим, что истинную функцию 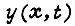находим, рассматривая совместно все движения звеньев рабочего органа робота, т. е. не разделяя их на основные и дополнительные. Для некоторой оптимальной траектории в пространстве имеем 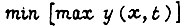Ему соответствует 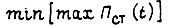в переходном процессе. Кроме того, разделяя движения, мы в состоянии создать y(x), данный момент времени t, отличающееся от y(x) в формуле (21) и имеющее вид

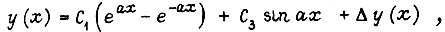
где 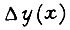уменьшает размах колебаний звена и обеспечивается добавочным управлением двигателя. Величине 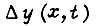соответствует приращение вращающего момента привода 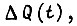которое без учета сил трения находим из формулы

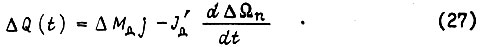
Анализ передаточных механических цепей, показанных на рис. 5, связан с учетом скручивания вращающихся валов. Механическая цепь с такими валами может быть составлена из типовых звеньев, изображенных на рис. 9.

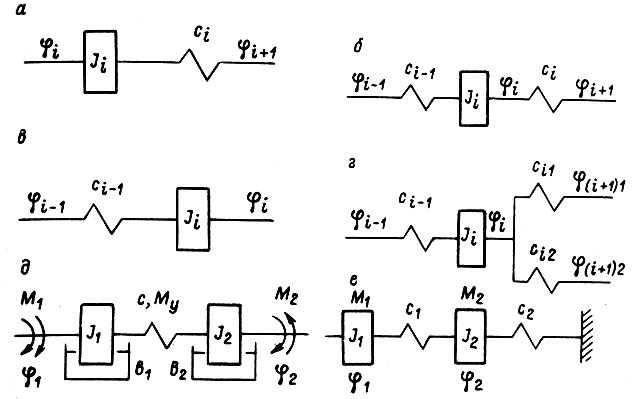
Рис. 9

Каждое из этих звеньев описывается дифференциальным уравнением:

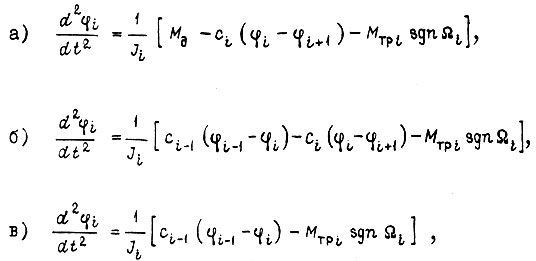
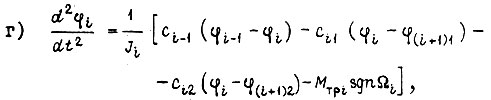
где 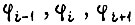- углы поворота участков валов; 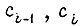коэффициенты крутильной жесткости; 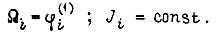Для схемы на рис. 9д имеем уравнения

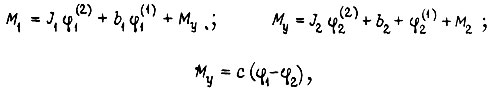
где 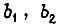- коэффициенты вязкого трения; 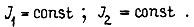В установившемся режиме вращения Расчетные двухмассовые (а в общем случае трех-четырехмассовые и т. д.) схемы на рис. 9 д, е берутся во внимание в зависимости от операции, выполняемой роботом. Схеме на рис. 9 е соответствует уравнение

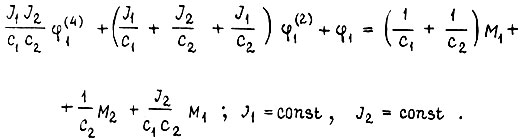
Здесь не учтены силы трения. При устранении заделки в стенку правого конца вала в схеме на рис. 9 е и при жестком конце справедливо уравнение

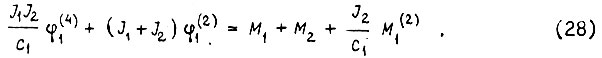
Подставляя в (28) формулу механической характеристики электродвигателя

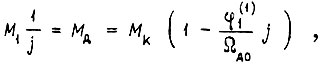
получаем

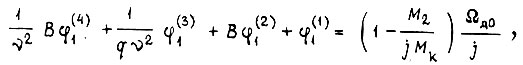
где

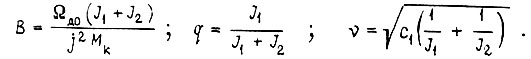
Момент M₂ учтен как момент сопротивления по отношению к M₁.

Уравнения для расчетных схем на рис. 9 записаны выше без учета волнового движения деформации упругих валов. Анализ волновых колебаний валов может быть проведен аналогично анализу колебаний изгиба звеньев рабочих органов роботов.

Пользуясь уравнениями расчетных схем (см. рис. 9), приводят к одному валу как моменты инерции отдельных участков цепи и моменты сил, так и коэффициенты жесткости упругих звеньев, исходя из закона сохранения энергии.

В приведенных выше уравнениях не отражено влияние кинематических погрешностей и зазоров в передачах между двигателем и шарниром рабочего органа. Неточность изготовления зубьев передач и эксцентриситеты являются причиной нарушения равномерности движения связываемых элементов. Передаточное число зацепления содержит малые периодические изменения около среднего значения. В общем случае выражение для мгновенного значения передаточного числа имеет вид

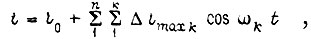
где 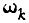- k-я частота возмущения передаточного числа; 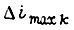k-я амплитуда гармонической составляющей; n - общее число зацеплений и валов в кинематической цепи.

Из всего спектра возмущений обычно целесообразно учитывать те, которые имеют наибольшие амплитуды, и те, которые наиболее близки к частоте свободных колебаний привода. Практически можно рассматривать случай, когда одно возмущение создает периодическое отклонение передаточного числа i от среднего значения i₀, т. е. 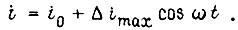Частота ω пропорциональна угловой скорости Ω одного из рассматриваемых валов редуктора, т. е. непостоянна. Однако изменениями Ω в течение периода изменения i можно пренебречь. Тогда текущее значение скорости Ω' есть сумма 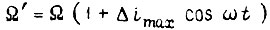а угол поворота 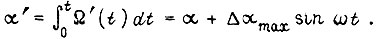В большинстве случаев пульсация передаточного числа не превышают 1-2%.

При учете влияния зазоров необходимо иметь в виду, что с течением времени они увеличиваются. Наибольшим зазором обладают выходные ступени зубчатых передач, понижающих скорость. Незатухающие колебания в следящих системах, вызванные наличием зазора в механической передаче, можно снизить путем уменьшения отношения момента инерции вала двигателя к моменту инерции механизма (после редуктора).

Иногда при построении механических цепей целесообразно учитывать максимально возможные параметры движений человеческих рук. Эти параметры приведены в табл. 1.

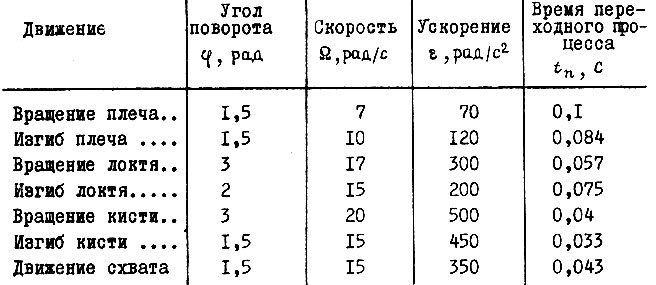
Таблица 1