4. Электрические цепи с двигателями переменного тока

Управление двигателями производится от автономных инверторов напряжения или тока. Для реверсивных приводов с диапазоном регулирования скорости свыше 20:1 и для следящих приводов независимо от их мощности целесообразно применение инверторов напряжения с широтно-импульсной модуляцией. Это обусловлено тем, что при питании двигателя от обычного инвертора без широтно-импульсной модуляции в зоне низких частот движение привода носит дискретный характер. При незначительном диапазоне регулирования частоты и напряженном повторно-кратковременном режиме работы привода целесообразно использование инверторов тока. На рис.20 изображена схема транзисторного инвертора. При использовании его как инвертора напряжения параллельно зажимам источника постоянного напряжения 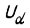подключается конденсатор C. В схеме транзисторного (или тиристорного) инвертора тока действует жесткая отрицательная обратная связь по току.

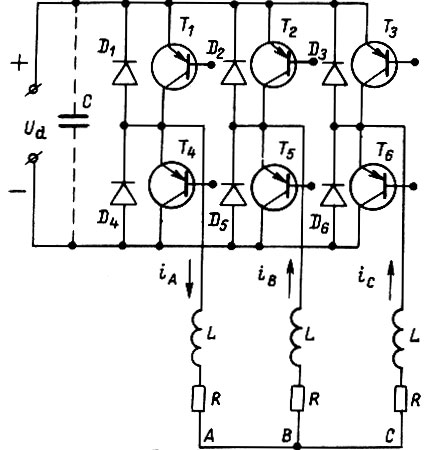
Рис. 20

В работе [13] показано, как следует в этом случае учитывать внутреннее сопротивление преобразователя выпрямитель-инвертор при расчете механических характеристик. Силовая часть привода переменного тока при правильном конструировании более надежна по сравнению со схемой постоянного тока. В особых условиях, например в пожароопасных, привод переменного тока предпочтительнее. Управление транзисторами или тиристорами инвертора производится от логических схем.

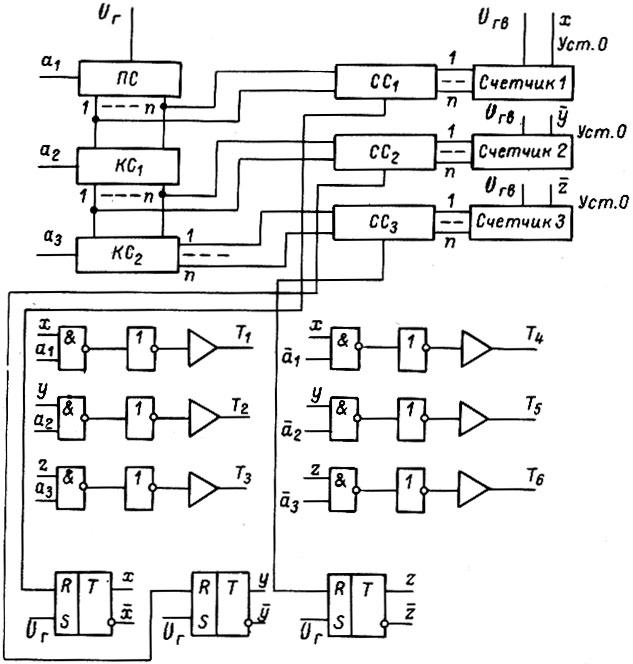
Рис. 21

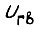На рис. 21 показано, как реализуется широтно-импульсная модуляция управляющих импульсов инвертора по синусному закону. На вход последовательностной логической схемы (ПС) поступают импульсы постоянной частоты , на входы счетчиков 1, 2, 3 - импульсы высокой частоты Двоичное число с n разрядами на выходе ПС изменяется вдоль временных тактов как полусинусоида. Числа на выходах комбинационных схем кс₁ и кс₂ сдвинуты относительно числа ПС соответственно на 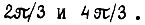Схемы сравнивают числа на выходах 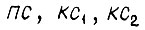и счетчиков. Если сравниваемые числа эквивалентны, то на выходе соответствующей схемы сравнения появляется "единица", переключающая свой SR-триггер в нулевое состояние. В единичное состояние триггеры устанавливаются импульсом 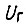. Состояние x = 1 соответствует включению транзисторов T₁ или T₄ (рис. 20), y = 1 - включению T₂ или 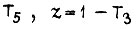или T₆. Транзисторы 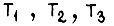включаются внутри положительных полуволн синусоид, а 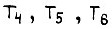- внутри отрицательных. Сигналы 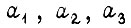указывают на полярность синусоид. Таким образом, частота напряжения на статорной обмотке двигателя определяется частотой 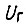, а напряжение - частотой .

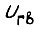Электромагнитный момент асинхронного двигателя вычисляют по формуле

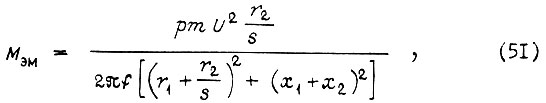
где p - число пар полюсов; m - число фаз обмотки статора; U - напряжение фазы статора; - активные и индуктивные сопротивления статорной и роторной (с учетом приведения) обмоток в Г-образной схеме замещения; f - частота питающей сети; - угловая скорость вращения ротора двигателя,

Для рабочей части характеристики 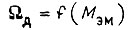справедлива зависимость

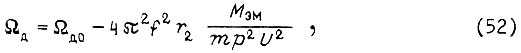
которая аналогична механической характеристике двигателя постоянного тока с независимым возбуждением. При управлении двигателем по закону 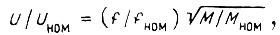где 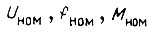- номинальные величины; M - момент механизма, получаем формулы электромагнитного момента [12]

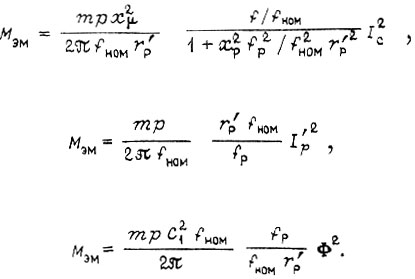
Здесь 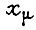- сопротивление намагничивания; 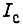- ток статора; 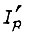- ток ротора; Φ - поток двигателя;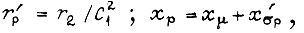 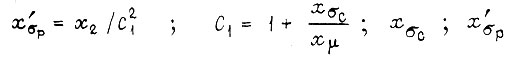сопротивления статора и ротора, связанные с потоками рассеивания; f_p - частота ротора. Из формул следует, что если не измерять момент M, а управление производить в функции только тона статора 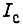, или тока ротора 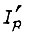, или потока Φ, то невозможно реализовать предложенный закон 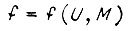При управлении от момента M необходимо ограничивать напряжение U как сверху, так и снизу, чтобы избежать тепловых перегрузок при больших моментах нагрузки и чрезмерно мягких естественных механических характеристик при малых.

Другой возможный закон управления двигателем есть

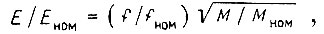
где E - э. д. с. статора. Это эквивалентно управлению с поддержанием постоянства относительной частоты ротора 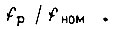При изменении входной координаты f скорость двигателя 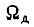изменяется независимо от изменения момента нагрузки в соответствии с формулой 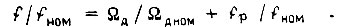Частотное управление асинхронным двигателем при 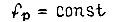является наиболее экономичным.

Однако реализация обратной связи по нагрузке довольно сложна. На практике часто используют управление, при котором 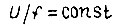либо поток 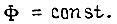В этих случаях потери в машине оказываются значительно большими.

Рабочий поток машины определяется намагничивающим током 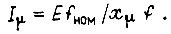Управление из условия 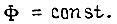соответствует частотному управлению согласно условию 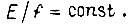Получение необходимой жесткости механических характеристик и уменьшенных потерь достигается в системе с инвертором напряжения, добавочно скорректированной по скорости вращения двигателя. Диапазон регулирования скорости зависит здесь от характера нагрузки. Этот диапазон более широк в системе с контуром стабилизации потока.

Для получения механической характеристики экскаваторного типа необходимо в системе с инвертором напряжения подать на его вход отрицательную задержанную обратную связь по абсолютному скольжению s. Исходя из уравнения рабочего участка механической характеристики асинхронного двигателя, питаемого синусоидальным напряжением:

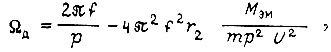
получаем при подстановке закона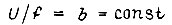

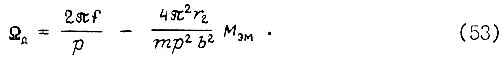
Отсюда момент воротного замыкания 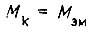при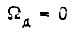

Подставляя его в уравнение движения i-го звена робота ((10)-(12)), получаем

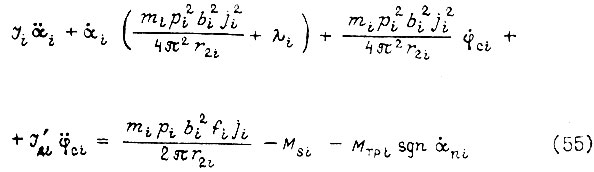
При наличии отрицательной обратной связи по скорости вращения двигателя 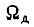частоту питания f представляем как разность: 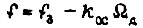где f₃ - частота от блока задания; 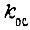- коэффициент обратной связи. Тогда

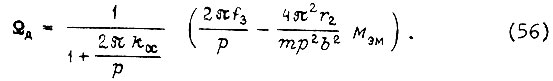
Если подать на вход системы привода частоту

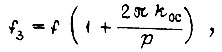
то получим скорость

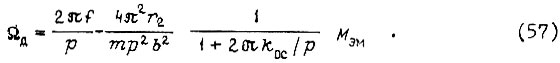
По сравнению с формулой (53) имеем меньшее падение скорости Ω при том же электромагнитном моменте двигателя. Момент короткого замыкания (57)

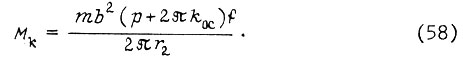
Приходим в уравнению движения i-го звена робота в динамике при 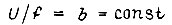и отрицательной обратной связи по скорости:

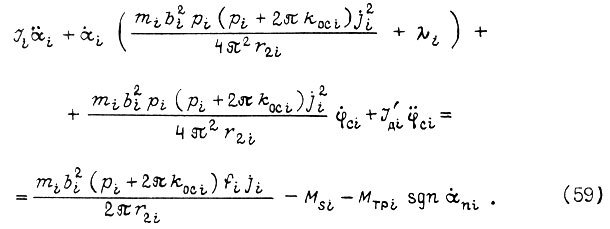
Для статического скручивания вала по схеме на рис. 9 д можно записать уравнение i-го звена аналогично (49), если заменить в ее левой части на на 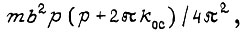а в правой - произвести ту же замену, но составляющую 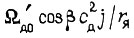заменить на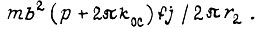

Управлению асинхронного электродвигателя со стабилизацией потока соответствует уравнение рабочей части характеристики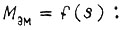

где 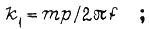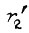- приведенное сопротивление ротора в T-образной схеме; 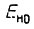- напряжение на намагничивающем контуре, соответствующее холостому ходу двигателя или принятому значению потока. Выразим скольжение s через скорость ротора 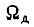. Тогда

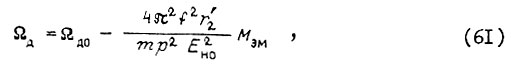
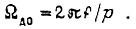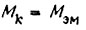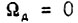где Отсюда момент короткого замыкания при есть

Подставляем (62) в общее уравнение движения i-го звена робота:

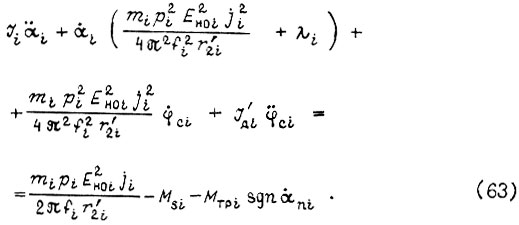
После включения связи по скорости

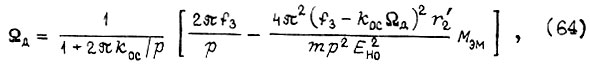
или

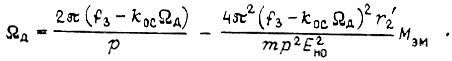
При сильной обратной связи 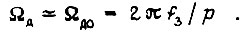Тогда

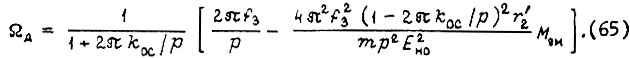
Если подать на вход системы привода частоту 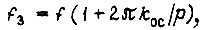то из (65) получаем

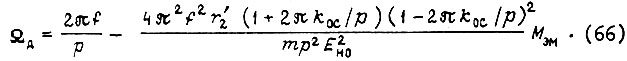
Момент короткого замыкания

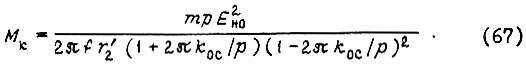
Приходим к уравнению относительно 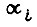звена робота

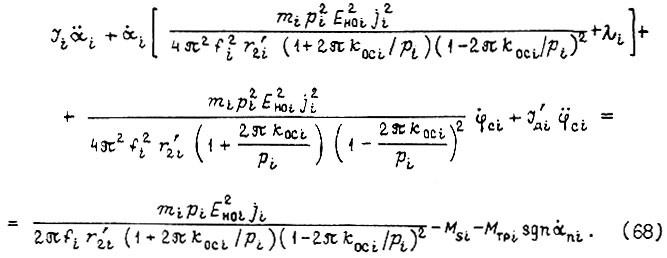
Движение звена робота с учетом упругой связи между двигателем и шарниром в случае стабилизации потока асинхронного двигателя можно описать аналогично уравнению (49).

Уравнения механических характеристик асинхронного двигателя (53), (56), (61), (64), (65) справедливы, если синусоидальна форма напряжения на статорной обмотке. Эта форма практически достигается при широтно-импульсной модуляции напряжения инвертора по синусному закону. Ненужность низких и стабильных скоростей перемещения звеньев робота означает устранение из привода блока, осуществляющего указанную модуляцию. Оценим неравномерность движения привода с асинхронным двигателем, вызванную ступенчатостью форм фазных напряжений на статорной обмотке.

Представим фазные напряжения, не зависящие от нагрузки, в виде

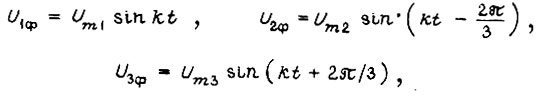
где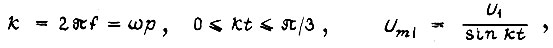

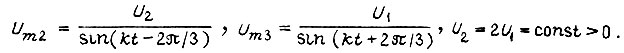
Такое представление соответствует включению обмотки статора по схеме треугольника. В каждый момент времени 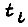имеем теперь систему несимметричных синусоидальных напряжений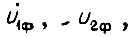 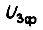с амплитудами 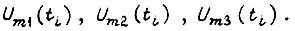Итак,к каждой фазе поступает синусоидальное напряжение постоянной частоты k с амплитудой, непостоянной во времени. Здесь ступенчатая форма фазного напряжения аппроксимируется синусоидой частоты k. Разложим несимметричную систему напряжений 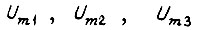для произвольного момента времени На две симметричные трехфазные системы: прямую и обратную. После разложения получаем формулы действующих значений напряжений:

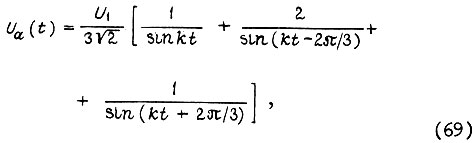
Связь между моментом 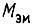и скольжением s в рассматриваемом случае описывается формулой

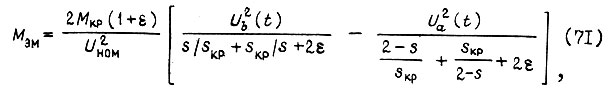
где 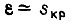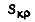- критическое скольжение; 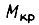- критический момент; 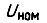- номинальное напряжение (синусоидальное). При малых скольжениях s, когда величинами 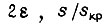по сравнению с 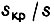и величиной s по сравнению с 2 можно пренебречь, получаем упрощенную формулу

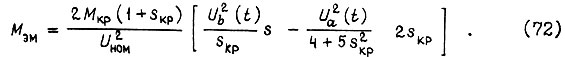
Отсюда при 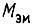не изменяющемся в установившемся движении, вытекает закон колебаний скольжения s во времени, вызванных ступенчатостью форм кривых напряжений 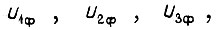который представляет собой частное решение дифференциального уравнения динамики электродвигателя:

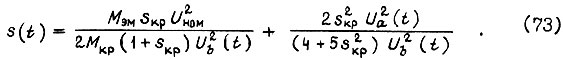
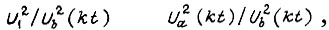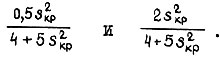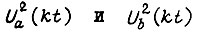На рис. 22 изображены функции которые показывают, что величина скольжения двигателя s(t) при заключена в интервале значений Этот вывод также справедлив для так как функции изменяются одинаково внутри каждого из участков:

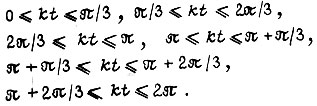
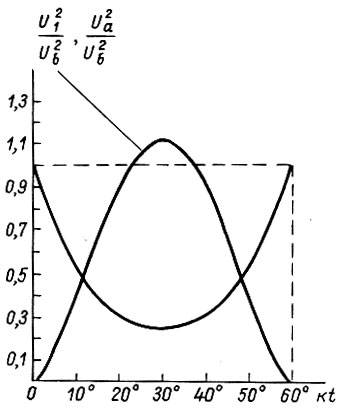
Рис. 22

Если 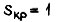то получаем максимум и минимум скольжения 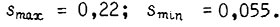Колебания скольжения возрастают при статическом моменте 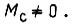Пусть для малой частоты 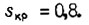Тогда получаем около моментов времени 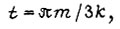где 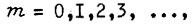величину скольжения 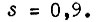Это соответствует периодической остановке двигателя, т. е. шаговому режиму вращения.

Дифференциальное уравнение, описывающее электромеханический переходный процесс асинхронного двигателя, имеет вид

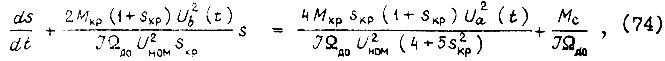
где 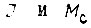- момент инерции и момент статической нагрузки привода, приведенные к валу электродвигателя и принимаемые неизменными. На каждом малом отрезке 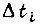где практически можно принять постоянными 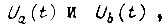приходим к решению

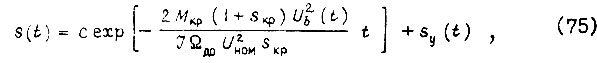
где 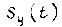определяется из (74); c - постоянная, зависящая от начальных условий на данном отрезке 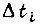. Разделим ось kt внутри 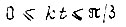на n малых отрезков величины которых определяются из условия

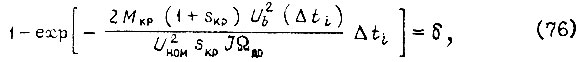
принимается одинаковой для всех 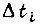. Скольжение s_r в конце отрезка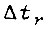

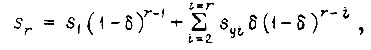
где 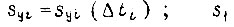- скольжение в конце 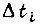. Приращение скольжения

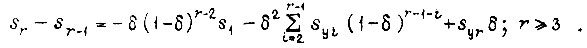
Очевидно, сумма всех абсолютных приращений скольжения на отрезках 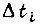внутри 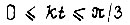есть удвоенный полный перепад скольжения 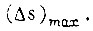Поэтому

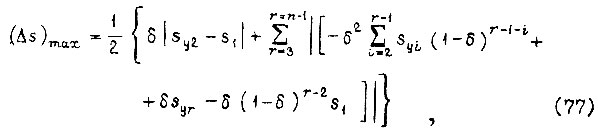
где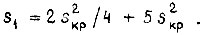

В формуле (77) не учитывается приращение скольжения на отрезках 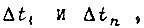являющихся крайними. Оценку величины 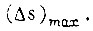производим, задав величину δ. При заданных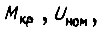 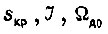из условия (76) находим для каждого 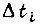величину 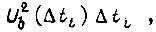а затем 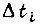. Зная величины 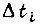, определяем число отрезков n. Вычислив все 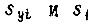по (74), получаем 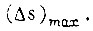Оценка неравномерности хода двигателя производится с учетом закона частотного управления, реализованного в структуре привода. Это означает,что для каждой частоты выходного напряжения инвертора величина 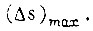вычисляется после того, как определена амплитуда напряжения инвертора U₁ для принятого закона управления.

Для приводов роботов могут быть использованы не только асинхронные, но и синхронные двигатели. В их число входят тихоходные машины с электромеханической редукцией. Имеется возможность на основе их строить приводы, у которых механические редукторы имеют меньшее передаточное число, что позволяет снизить колебательность в движениях при наличии упругих деформаций механических цепей. Применение этих машин целесообразно, если они имеют удовлетворительные весогабаритные показатели. Известен способ частотно-токового управления машинами переменного тока с целью получения приводов с управляемыми моментами [14]. В этом случае момент не зависит от частоты вращения вала и механические характеристики получаются предельно мягкими. При частотно-токовом управлении в обмотки электрической машины задаются токи, мгновенные значения которых определяются входным сигналом, т. е. требуемым моментом и угловым положением ротора.

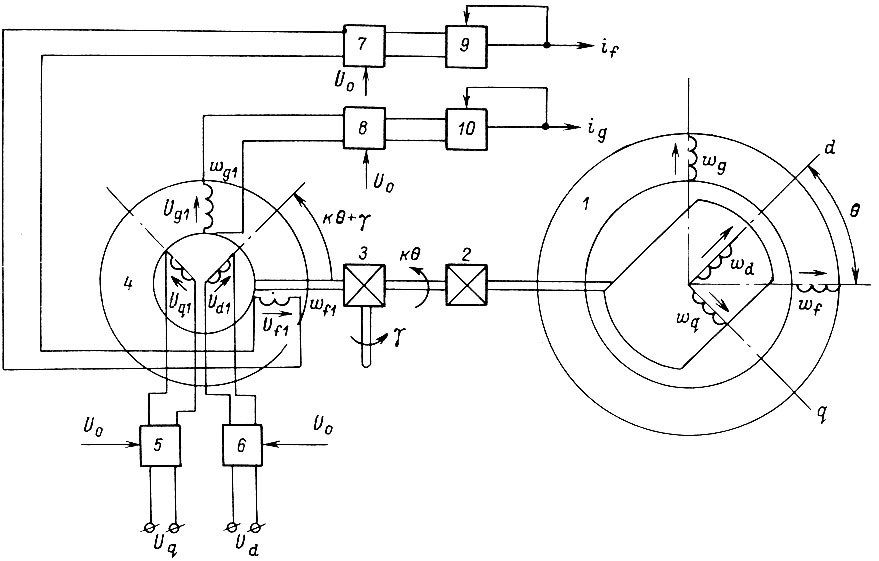
Рис. 23

На рис. 23 представлена схема обобщенного привода с частотно-токовым управлением, в котором осуществляется формирование токов в обмотках двигателя. Ротор двухфазной двухполюсной машины 1 связан через редуктор 2 с коэффициентом редукции k и через дифференциал 3 с ротором датчика углового положения 4. Поворот второго входного вала дифференциала 3 на угол γ осуществляется внешним контуром привода. Ротор датчика 4 поворачивается на угол, равный сумме углов kθ и γ. В качестве датчика углового положения γ использована электрическая машина типа синусно-косинусного вращающегося трансформатора. Машина 4 выбрана двухполюсной. 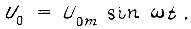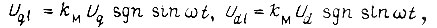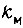На входы модуляторов 5 и 6 подаются сигналы и опорное напряжение На выходах модуляторов где - статический коэффициент передачи модулятора. Напряжения 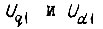поступают на роторные обмотки 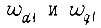датчика 4. Со статорных обмоток 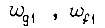снимаем напряжения

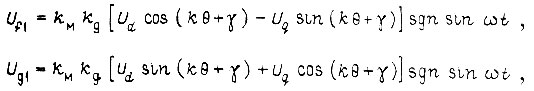
где 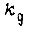- статический коэффициент передачи напряжения от ротора к статору датчика 4 при условии, что 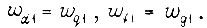Затем напряжения 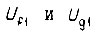поступают на выходы фазочувствительных выпрямителей 7 и 8 с опорным напряжением 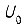Устройства 9 и 10 являются усилителями тока. Усилитель тока - это усилитель напряжения, охваченный жесткой отрицательной обратной связью по выходному току.

Отметим, что в реальном устройстве сложение углов 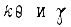может быть осуществлено не с помощью механического дифференциала 3, а с помощью, например, дифференциальной индукционной машины [14]. Схема на рис. 23 является общей в том смысле, что охватывает системы привода с синхронными и асинхронными двигателями. В приводе с частотно-токовым управлением синхронной машиной достаточно принять 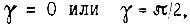при этом сигналы 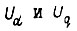меняются местами. Но это означает, что в данном случае можно обойтись без дифференциала. В приводе с асинхронной машиной для получения момента при любой угловой скорости ротора необходимо создать дополнительную скорость поля статора по отношению к скорости ротора. Это обеспечивается путем изменения угла γ с нужной скоростью.

В приводах с управляемым моментом на базе синхронных и асинхронных машин, используемых в замкнутых системах регулирования, не. могут возникать такие режимы, в которых синхронная машина выпадает из синхронизма, а асинхронная - опрокинется. Это справедливо для любого характера изменения входного сигнала и нагрузки на валу. Заметим, что в месте соединения звеньев робота одно звено может быть непосредственно статором, а другое - ротором двигателя.

В схемах роботов находят применение шаговые электродвигатели. Если двигатель является силовым исполнительным элементом, то он самостоятельно перемещает i-е звено рабочего органа в одну из требуемых позиций. В другом варианте шаговый двигатель выполняет функцию преобразования импульсного сигнала в угловое или линейное перемещение устройства, управляющего силовым исполнительным элементом. Это может быть, например, золотник гидроусилителя. В работе [15] рассмотрены физика и управление шаговыми электродвигателями.