
2. Переходный процесс в контуре регулирования
Дифференциальное уравнение переходного процесса в контуре регулирования, представленном линейным и непрерывным, имеет вид
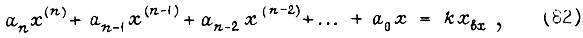
где х - сигнал выхода контура, изменяющийся во времени 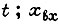 - сигнал входа;
- сигнал входа; 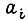 - постоянные коэффициенты; k - коэффициент усилия разомкнутого контура.
- постоянные коэффициенты; k - коэффициент усилия разомкнутого контура.
Предположим, что контур состоит из усилительных и n апериодических звеньев. Воспользовавшись преобразованием Лапласа-Карсона
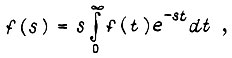
получаем передаточную функцию апериодического звена
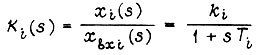
и передаточную функции разомкнутого контура регулирования
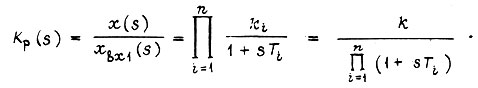
Здесь 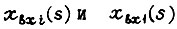 - изображения сигналов входа соответственно i-го звена и разомкнутого контура;
- изображения сигналов входа соответственно i-го звена и разомкнутого контура; 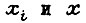 сигналы выходов;
сигналы выходов; 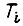 - постоянная времени апериодического звена; произведение всех
- постоянная времени апериодического звена; произведение всех 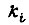 учитывает присутствие в контуре апериодических и усилительных звеньев. При
учитывает присутствие в контуре апериодических и усилительных звеньев. При 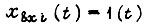 - единичной ступенчатой функции, существующей в области
- единичной ступенчатой функции, существующей в области 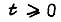 , имеем равенство
, имеем равенство 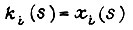 и переходную функцию i-го звена
и переходную функцию i-го звена
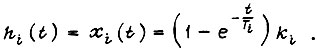
Заменим 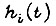 функцией, приближающейся к ней с точностью, удовлетворительной для инженерной практики:
функцией, приближающейся к ней с точностью, удовлетворительной для инженерной практики:
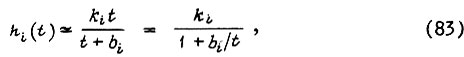
где 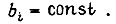 Тогда для времени
Тогда для времени 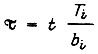
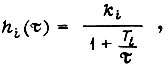
причем для всех апериодических звеньев 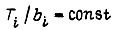 что связано с выбранной аппроксимацией выходной реакции апериодического звена на появление сигнала
что связано с выбранной аппроксимацией выходной реакции апериодического звена на появление сигнала 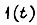 на его входе.
на его входе.
Из вида 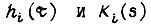 следует, что преобразование Лапласа - Карсона для функции
следует, что преобразование Лапласа - Карсона для функции 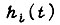 сводится к замене
сводится к замене 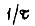 в формуле
в формуле 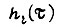 на параметр s, что справедливо, если
на параметр s, что справедливо, если 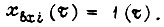
Передаточная функция разомкнутого контура 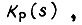 как известно, может быть представлена в виде суммы
как известно, может быть представлена в виде суммы
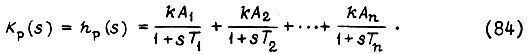
Перейдя во временную область, получаем с учетом аппроксимации h-функций
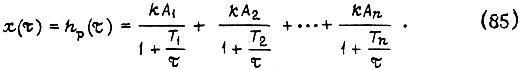
где 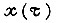 - сигнал выхода разомкнутого контура при
- сигнал выхода разомкнутого контура при 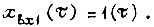 Очевидно, последнюю формулу
Очевидно, последнюю формулу 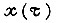 можно переписать следующим образом:
можно переписать следующим образом:
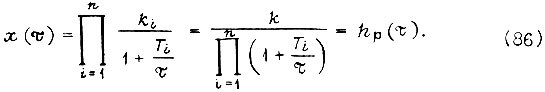
Таким образом, переход к 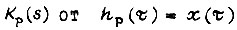 - переходной функции разомкнутого контура - сводится также к замене
- переходной функции разомкнутого контура - сводится также к замене 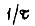 в формуле
в формуле 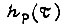 на параметр s.
на параметр s.
Дифференциальному уравнению переходного процесса в замкнутом контуре регулирования (82) соответствует передаточная
функция K(s) при 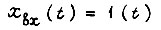
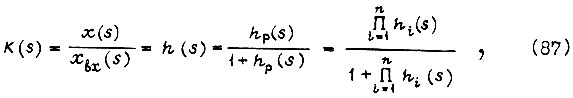
где 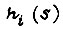 - изображение сигнала
- изображение сигнала 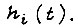
Вывод, сделанный выше о замене 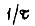 на s (справедлив и обратный переход) для апериодического звена и последовательной разомкнутой цепи, состоящей из n звеньев, можно применить к функции K(s), описывающей устойчивую систему, если переходная функция замкнутого контура равна сумме экспоненциальных функций. Для рассмотрения же общего случая воспользуемся известной формулой
на s (справедлив и обратный переход) для апериодического звена и последовательной разомкнутой цепи, состоящей из n звеньев, можно применить к функции K(s), описывающей устойчивую систему, если переходная функция замкнутого контура равна сумме экспоненциальных функций. Для рассмотрения же общего случая воспользуемся известной формулой 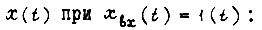
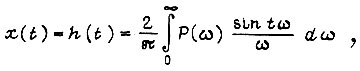
где 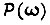 - действительная часть амплитудно-фазовой частотной характеристики замкнутого контура регулирования
- действительная часть амплитудно-фазовой частотной характеристики замкнутого контура регулирования 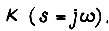
Для разомкнутого контура действительную часть 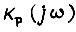 получаем из (84) в виде
получаем из (84) в виде
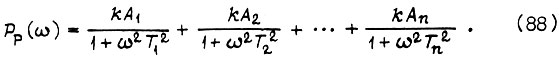
Для замкнутого контура из формулы (87) с учетом (82)
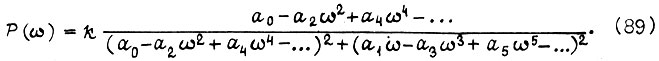
Здесь 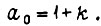 Если переходную функцию апериодического звена
Если переходную функцию апериодического звена 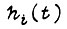 аппроксимировать не так, как показано в формуле (83), а в виде
аппроксимировать не так, как показано в формуле (83), а в виде
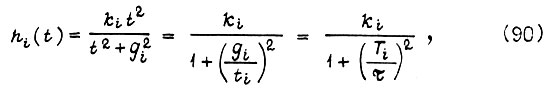
где 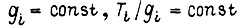 для всех звеньев,
для всех звеньев, 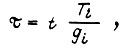 то получим, учитывая (88) и (90):
то получим, учитывая (88) и (90):

при 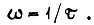 Тогда
Тогда
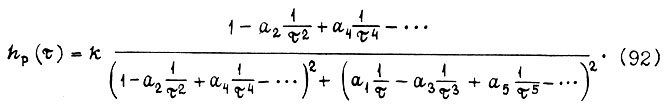
Предположим, что существуют такая действительная часть амплитудно-фазовой частотной характеристики некоторой разомкнутой системы, состоящей из апериодических и усилительных звеньев, равная 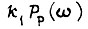 и время
и время 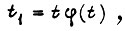 что соблюдается равенство
что соблюдается равенство
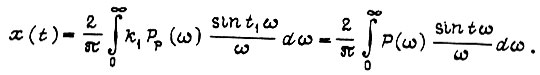
Здесь 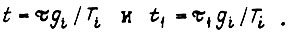
Подынтегральную функцию второго интеграла перепишем следующим образом:
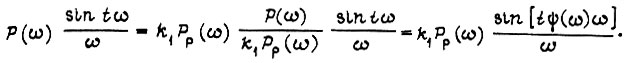
Функцию 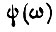 находим из условия
находим из условия
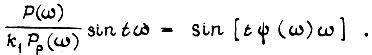
Она имеет вид
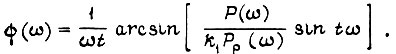
Так как обязательно соблюдение равенства 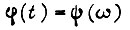 то
то
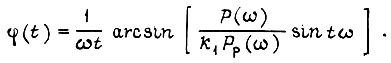
Переходный процесс в разомкнутой системе при ступенчатом воздействии на входе в соответствии с вышеизложенным описывается функцией 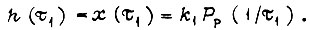 тогда из формулы
тогда из формулы 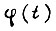 получаем при
получаем при 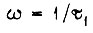
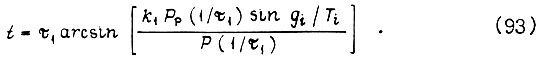
Таким образом, располагая формулами 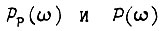 и считая, что на выходе замкнутой системы переходный процесс описывается как
и считая, что на выходе замкнутой системы переходный процесс описывается как 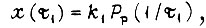 находим истинное время t, пользуясь соотношением (93), устанавливающим связь между
находим истинное время t, пользуясь соотношением (93), устанавливающим связь между 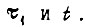
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'