3. Устойчивость контура регулирования

Рассмотрим замкнутый контур, состоящий из апериодических и усилительных звеньев. Передаточную функцию апериодического звена 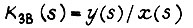где - изображения по Лапласу - Карсону выходного и входного сигналов, запишем следующим образом: 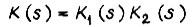где 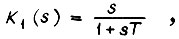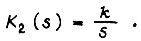Для единичного ступенчатого воздействия, приложенного при t = 0 к входу звена k₁ с передаточной функцией 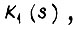выходной сигнал звена есть 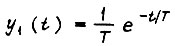Введем новое время 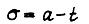где 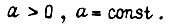Вдоль оси σ сигнал 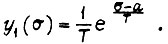Эта функция приближается к 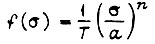на участке 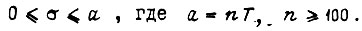Функция 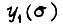заключена на участке 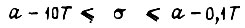при n = 100 между 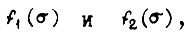где

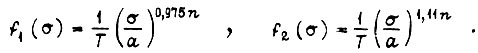
Здесь вычисление 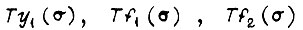произведено до четвертого знака после числа целых. На участках 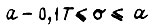и условие 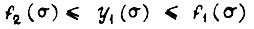не соблюдается. Однако, воспользовавшись им для времени 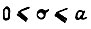после проверки вычислениями получаем, что ошибка такого представления переходных функций звеньев k₁ приведенная к выходу цепи га последовательно соединенных апериодических звеньев, составляет в переходном процессе не более 0,03 от максимального значения сигнала выхода. Это справедливо, если m≤50 . Изображение

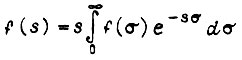
функций 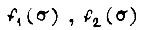есть

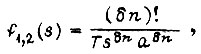
где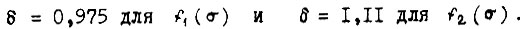

Формула 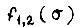с учетом аппроксимации 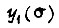есть формула граничных передаточных функций, описывающих процессы, внутри которых заключен переходный процесс звена k₁ вдоль оси σ на участке 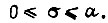Граничные передаточные функции цепи m последовательно соединенных звеньев k₁ имеют вид

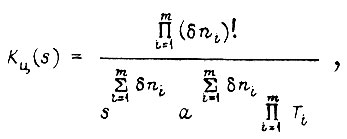
где 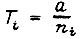- постоянная времени i-го апериодического звена. Перепишем функцию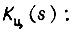

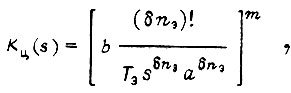
введя обозначения

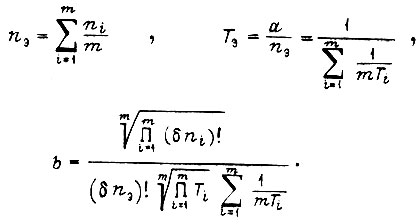
Из выражения 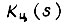следует, что последовательная цепь m звеньев k₁ с различными постоянными 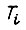и последовательная цепь m звеньев k₁, с одинаковыми постоянными, равными 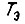имеют одни и те же граничные передаточные функции, получаемые из 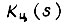подстановкой 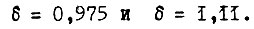Переходная функция звена 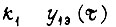с постоянной 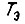, как следует из формулы 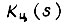и способа аппроксимации 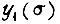ограничивается на участке 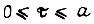функциями

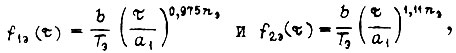
где 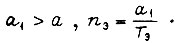Переменную τ представим следующим образом: 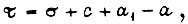c - постоянная. Запишем 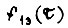и 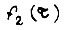в общем виде

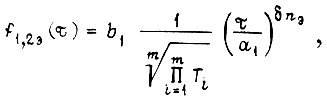
где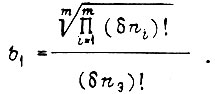

Переходная функция 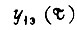есть

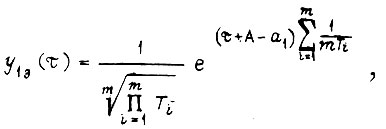
где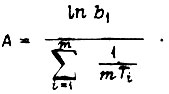

Принимаем 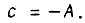Тогда

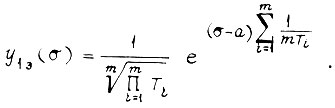
Так как для 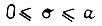справедливо неравенство

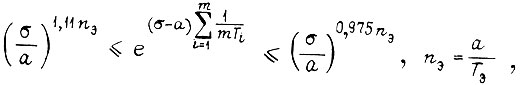
то

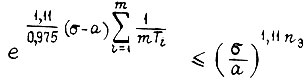
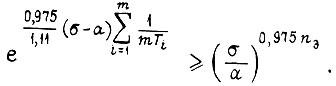
Следовательно, передаточная функция последовательной цепи m звеньев k₁ с одинаковыми постоянными времени, равными 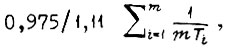и передаточная функция аналогичной цепи с постоянными времени, равными 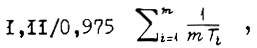описывают переходные процессы, внутри которых заключены процессы, описываемые граничными передаточными функциями, получаемыми из формулы для 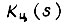. Поэтому, с учетом 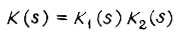получаем, что переходный процесс последовательной цепи m апериодических звеньев с постоянными времени 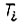заключен между двумя процессами, которым соответствует передаточная функция разомкнутой цепи апериодических звеньев с постоянными времени, равными 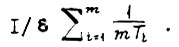Формула функции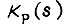

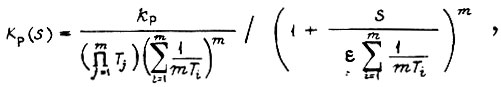
где 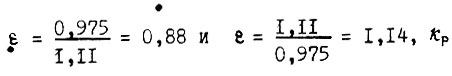- коэффициент передачи разомкнутой цепи. Передаточной функции 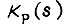соответствует передаточная функция 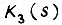замкнутой цепи, образующей линейный контур регулирования

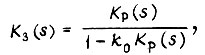
где k₀ - коэффициент обратной связи. При отрицательной обратной связи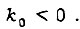

В результате после подстановки 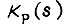в 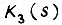находим, что переходный процесс в линейном контуре регулирования, состоящем из m апериодических звеньев, заключен между двумя функциями, определяемыми по формуле

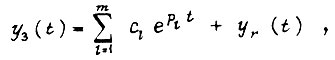
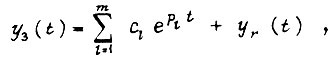
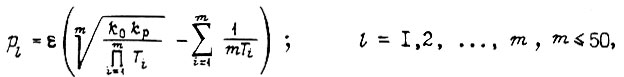
где 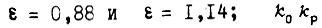- коэффициент передачи разомкнутого контура; 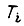- постоянная времени i-го звена; 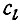- постоянные, определяемые из начальных условий; 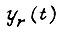частное Решение дифференциального уравнения переходного процесса.

Контур регулирования устойчив, если соблюдается неравенство

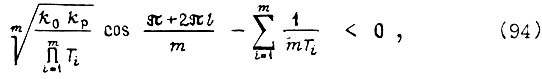
где 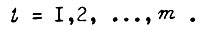Из всех значений косинусоидальной функции, получаемых при подстановке l, следует брать максимальное положительное.

Рассмотрим теперь одностепенную систему привода робота с параллельной коррекцией. Ее передаточную функцию запишем в виде

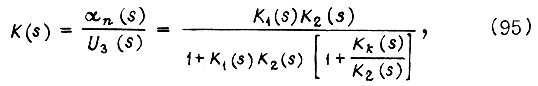
где 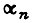- выходной сигнал замкнутой системы, пропорциональный углу поворота вала привода (либо линейному перемещению); 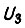- задающий сигнал; 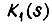- передаточная функция части канала прямой передачи, охваченной параллельным корректирующим звеном с передаточной функцией 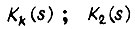- передаточная функция части канала, неохваченной корректирующим звеном.

Для линеаризованного канала прямой передачи

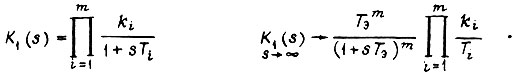
Электродвигатель может быть представлен одним или двумя апериодическими звеньями или как колебательное звено. Допустим, что с помощью аппроксимации переходной функции колебательного звена при времени оно заменяется апериодическими звеньями. Тогда получаем

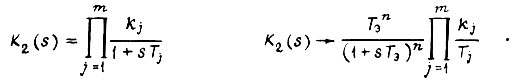
Здесь зависимость пути от скорости движения учтена в апериодическом звене. Для передаточной функции корректирующего звена

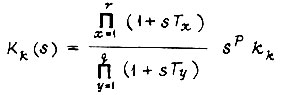
отношение

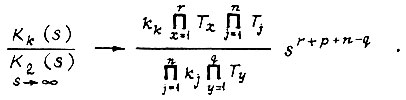
Передаточная функция системы с учетом 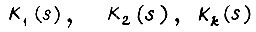при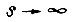

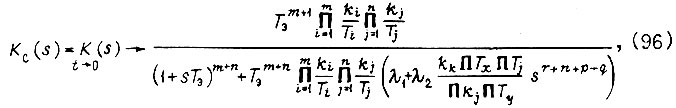
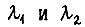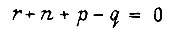
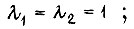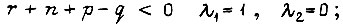где значения выбираем по правилу: при при при 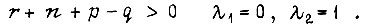Воспользуемся выражением 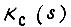для расчета переходного процесса на каждом из отрезков длительностью 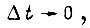которой дискретизирована ось времени. Для всех этих отрезков, кроме первого, начальные условия не являются нулевыми. Поэтому отношение изображений сигналов 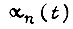и и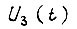 при отсчете времени от начала отрезка есть сумма 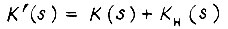или для 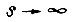упрощенно: 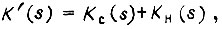где 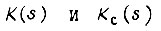определяются соответственно из формул (95) и (96). Добавочная составляющая 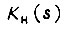учитывает неравенство нулю начальных условий и представляет собой степенной полином, стремящийся к нулю при 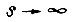. Выбираем постоянную времени 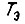такой, чтобы частное решение дифференциального уравнения исполнительной системы с единичным входным сигналом 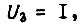полученное из выражения 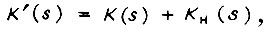совпало на каждом отрезке длительностью Δt с частным решением уравнения, соответствующего функции 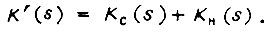Это значит, что надо найти 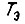из условия 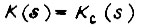при .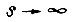

После определения 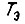получаем корни характеристического уравнения системы на отрезке Δt:

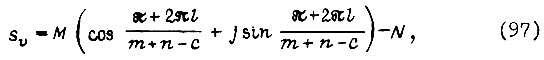
где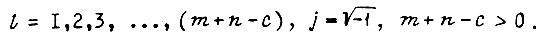

Коэффициенты М, N, с равны:

при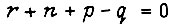

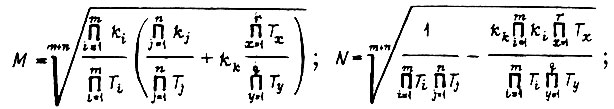
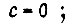
при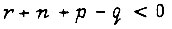

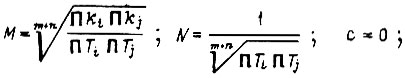
при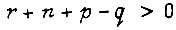

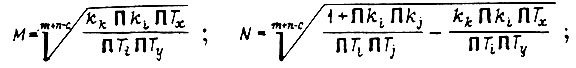
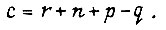
Переходный процесс в системе внутри отрезка 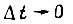описывается уравнением

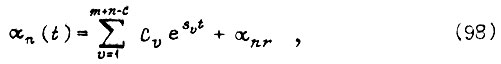
где 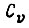- коэффициенты, определяемые из начальных условий отрезка и уравнения движения неаппроксимированной системы; частное решение 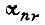одинаково на всех отрезках 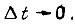В устойчивой системе 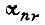и коэффициенты 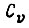принимают конечные значения. Следовательно, если исполнительная система устойчива, то выполняется в соответствии с (97) условие

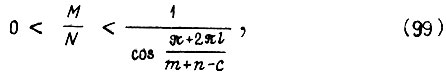
где из всех значений косинусоидальной функции следует учитывать только максимальное положительное.

Исследуя устойчивость одностепенной системы привода для робота известной конструкции, устанавливаем при этом допустимое соотношение между ее параметрами. Это соотношение ограничивает точность воспроизведения заданного пути или скорости проходимых рассматриваемым звеном конструкции в установившемся движении. На ошибку воспроизведения задания влияет величина силы или момента силы сопротивления, действующих совместно с движущей силой (моментом силы) привода. В общем случае сила сопротивления есть результат взаимодействия движений звеньев всех степеней подвижности робота. Тогда анализ переходных процессов и характера установившихся ошибок значительно усложняется.

Наличие в структуре системы привода обратной связи по усилию в шарнире с целью компенсации его влияния на движение привода рассматриваемой степени подвижности позволяет более эффективно применить результаты исследования устойчивости системы. Теперь, оценивая установившиеся ошибки воспроизведения задания и исходя из оценок устойчивости одностепенной системы привода, можно не учитывать взаимовлияния переходных процессов разных степеней подвижности робота, если связь по усилию действует идеально. Практически, как известно, можно получить частичную инвариантность к изменениям силы сопротивления. Информацию о моменте силы сопротивления получаем, измерив момент силы, развиваемой двигателем, и ускорение его вала.

Учет ограничений по мощности, которую могут развивать реальные, источники питания системы привода, приводит при исследовании устойчивости к рассмотрению вместо случая, когда при 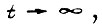у двух других нежелательных режимов. В первом режиме система переходит в некоторое предельное состояние 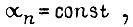, из которого она не может выйти, а во втором - устанавливаются незатухающие колебания. Параметры системы привода, полученные из условия отсутствия этих режимов в известной структуре , характеризуют наименьшие ошибки воспроизведения заданий по пути и скорости, которые можно получить. Желаемая область параметров может быть установлена, если воспользоваться результатами § 2 гл. 2.