
4. Линейный синтез системы привода
В общем случае действительную часть частотной характеристики системы 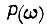 находим, задав
находим, задав 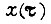 в соответствии с (93). Ниже рассматривается упрощенный подход к частотному синтезу.
в соответствии с (93). Ниже рассматривается упрощенный подход к частотному синтезу.
Для схемы привода, изображенной на рис.30, коэффициент усиления усилителя рассчитывается из условия обеспечения номинальной скорости двигателя при номинальной нагрузке и заданной допустимой ошибке рассогласования 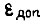 между сигналами
между сигналами 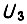 и
и 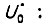

где  - номинальное напряжение силового преобразователя
- номинальное напряжение силового преобразователя 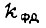 - коэффициент передачи фазового детектора;
- коэффициент передачи фазового детектора; 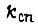 - коэффициент передачи преобразователя.
- коэффициент передачи преобразователя.
Передаточная функция разомкнутой системы привода
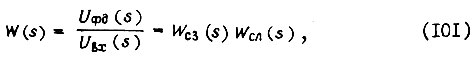
где
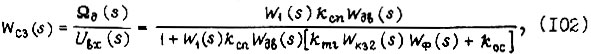
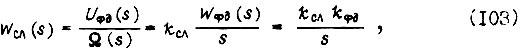
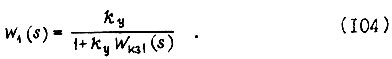
Здесь 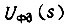 напряжение выхода фазового детектора;
напряжение выхода фазового детектора; 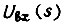 - напряжение входа разомкнутой системы привода (см. рис. 30);
- напряжение входа разомкнутой системы привода (см. рис. 30); 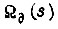 - угловая скорость вращения вала двигателя;
- угловая скорость вращения вала двигателя; 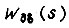 - передаточная функция двигателя;
- передаточная функция двигателя; 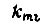 - коэффициент передачи тахогенератора;
- коэффициент передачи тахогенератора; 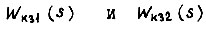 - передаточные функции корректирующих звеньев
- передаточные функции корректирующих звеньев 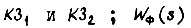 - передаточная функция усилителя, охваченного обратной связью;
- передаточная функция усилителя, охваченного обратной связью; 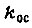 - коэффициент жесткости отрицательной обратной связи по скорости
- коэффициент жесткости отрицательной обратной связи по скорости 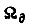 Управлением со стороны ВУ изменяются параметры звеньев
Управлением со стороны ВУ изменяются параметры звеньев 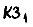 и
и 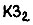 с целью получения одинаковых динамических свойств системы привода внутри различных отрезков времени.
с целью получения одинаковых динамических свойств системы привода внутри различных отрезков времени.
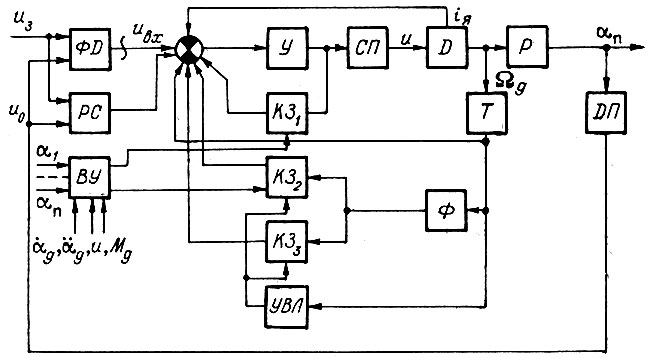
Рис. 30
Частота среза для функции 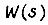 в системах с двигателями обычного исполнения (исключая малоинерционные двигатели с гладким или печатным якорем) ограничивается величиной порядка
в системах с двигателями обычного исполнения (исключая малоинерционные двигатели с гладким или печатным якорем) ограничивается величиной порядка 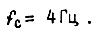 В системе с люфтом для уменьшения времени успокоения сдвиг фазы
В системе с люфтом для уменьшения времени успокоения сдвиг фазы 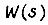 на частоте среза не должен превышать 110-120°, что практически обеспечивает апериодический характер процессов [16]. Находим
на частоте среза не должен превышать 110-120°, что практически обеспечивает апериодический характер процессов [16]. Находим 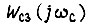 по формуле
по формуле
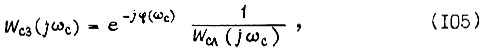
где 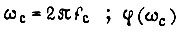 - допустимый фазовый сдвиг для функции
- допустимый фазовый сдвиг для функции 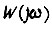 на частоте
на частоте 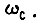
Представим приближенно функцию 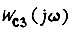 на частоте
на частоте 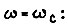
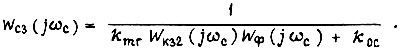
Тогда 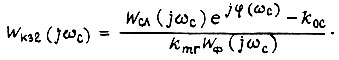
Задав передаточную функцию 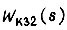 в виде
в виде
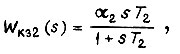
получаем 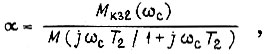 где
где 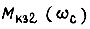 - модуль числа
- модуль числа 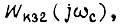 а
а 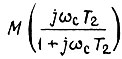 - модуль числа
- модуль числа 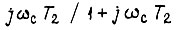 Постоянная
Постоянная 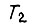 определяется из равенства
определяется из равенства
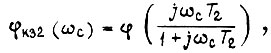
где 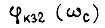 - фаза числа
- фаза числа 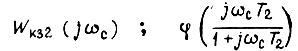 - фаза числа
- фаза числа 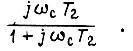 При расчете системы привода (см. рис. 30) необходимо также обеспечить запасы по модулю и фазе контура, образованного обратной связью по скорости двигателя
При расчете системы привода (см. рис. 30) необходимо также обеспечить запасы по модулю и фазе контура, образованного обратной связью по скорости двигателя 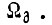 . В работе [16] указывается на то, что передаточная функция разомкнутого скоростного контура должна удовлетворять требованию по величине модуля на частоте
. В работе [16] указывается на то, что передаточная функция разомкнутого скоростного контура должна удовлетворять требованию по величине модуля на частоте 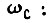
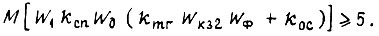
При этом на частоте 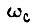 достаточно иметь запас по фазе 30°. Минимальное значение частоты среза для передаточной функции разомкнутого скоростного контура может быть выше частоты среза аналогичной функции внешнего контура в 2-3 раза при модуле, равном 5. Увеличение этого модуля приводит к уменьшению помехозащищенности системы привода. Число
достаточно иметь запас по фазе 30°. Минимальное значение частоты среза для передаточной функции разомкнутого скоростного контура может быть выше частоты среза аналогичной функции внешнего контура в 2-3 раза при модуле, равном 5. Увеличение этого модуля приводит к уменьшению помехозащищенности системы привода. Число 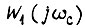 находим по формуле
находим по формуле
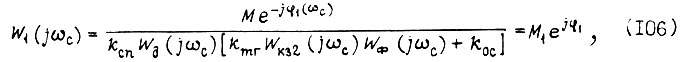
где 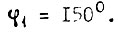
Задав передаточную функцию звена 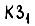 в виде
в виде
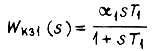
и считая, что на частоте 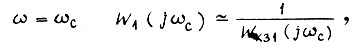 получаем
получаем 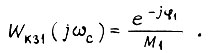 Тогда
Тогда
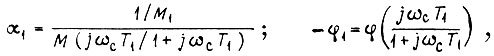
где 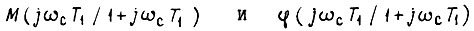 - модуль и фаза числа
- модуль и фаза числа 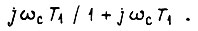
Если в качестве силового преобразователя применен тиристорный выпрямитель, то он может быть представлен линейным звеном при арккосинусном управлении и включении перед ним звена с насыщением и апериодического звена с постоянной времени 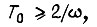 где
где 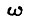 - угловая частота питающей сети. Тогда преобразователь является полностью безынерционным, если число фаз выпрямителя
- угловая частота питающей сети. Тогда преобразователь является полностью безынерционным, если число фаз выпрямителя 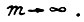 Неучет конечного значения
Неучет конечного значения 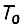 допускается, если
допускается, если 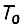 значительно меньше электромеханической постоянной привода. Применение звена с насыщением и апериодического звена помогает также устранению динамических уравнительных токов реверсивного выпрямителя.
значительно меньше электромеханической постоянной привода. Применение звена с насыщением и апериодического звена помогает также устранению динамических уравнительных токов реверсивного выпрямителя.
Системы привода постоянного и переменного тока исследуются как непрерывные до тех пор, пока амплитудой пульсации скорости вала двигателя можно пренебречь по сравнению с заданной скоростью.
Неучет задержанной связи по току якоря либо по скольжению ротора асинхронного двигателя означает, что в процессе пуска и реверса привод не будет обладать тем быстродействием, которое гарантирует синтезированные параметры корректирующих звеньев.
Системы привода, в которых силовой преобразователь является источником тока, относятся к системам, отрабатывающим задания по моментам или силам. Общий подход к их синтезу остается тем же.
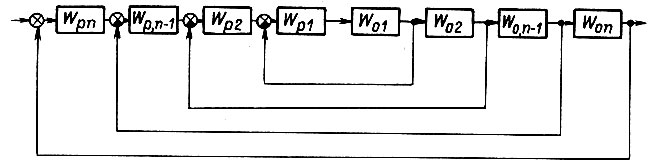
Рис. 31
Выше рассмотрен способ управления с параллельной коррекцией. Другим способом является управление с подчиненными контурами. На рис. 31 приведена схема с подчиненными регулированием, состоящая из n контуров. Объект регулирования разбивают на n, частей, каждая из которых имеет на своем выходе соответствующую регулируемую величину. Как правило, такая часть объекта регулирования характеризуется одной большой постоянной времени, компенсируемой действием своего регулятора. Любой из контуров системы является внешним (управляющим) по отношению к одному из контуров 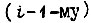 и внутренним (подчиненным) по отношению к другому
и внутренним (подчиненным) по отношению к другому 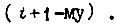 Исключение составляют два крайних контура. Настройка многоконтурной системы с подчиненным регулированием достигается последовательной оптимизацией контуров, начиная с внутреннего и кончая внешним.
Исключение составляют два крайних контура. Настройка многоконтурной системы с подчиненным регулированием достигается последовательной оптимизацией контуров, начиная с внутреннего и кончая внешним.
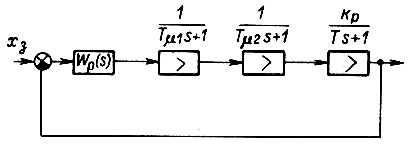
Рис. 32
Пусть в контуре (рис. 32) объект регулирования характеризуется коэффициентом передачи 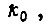 одной большой
одной большой 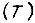 и двумя малыми
и двумя малыми 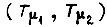 постоянными времени. Представим два звена с постоянными
постоянными времени. Представим два звена с постоянными 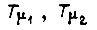 передаточной функцией
передаточной функцией
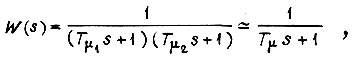
где 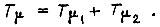 Передаточная функция объекта регулирования
Передаточная функция объекта регулирования
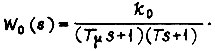
Выберем передаточную функцию регулятора вида
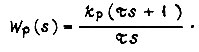
При 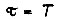 передаточная функция разомкнутого контура равна
передаточная функция разомкнутого контура равна
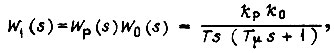
а замкнутого -
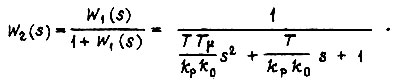
Считая, что 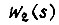 характеризует колебательное звено, перепишем ее в виде
характеризует колебательное звено, перепишем ее в виде
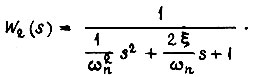
Переходная функция 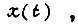 соответствующая
соответствующая 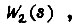 имеет вид
имеет вид 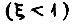
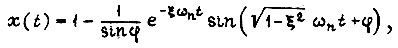
где 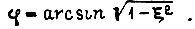 При
При 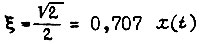 характеризуется перерегулированием
характеризуется перерегулированием 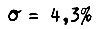 (рис. 33). Время
(рис. 33). Время 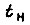 равно
равно 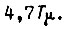
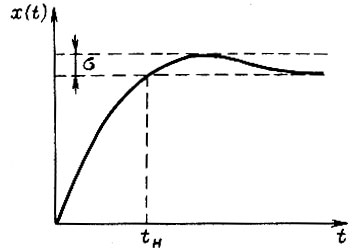
Рис. 33
Поскольку 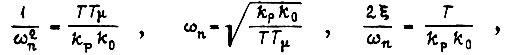
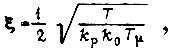 то при
то при 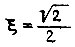 получаем
получаем
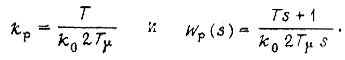
Тогда передаточная функция замкнутого контура
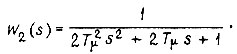
Итак, поведение замкнутого оптимизированного контура определяется лишь суммой малых постоянных времени 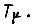 Данная настройка контура называется настройкой по "модульному критерию" частотной характеристики, для которого
Данная настройка контура называется настройкой по "модульному критерию" частотной характеристики, для которого
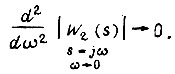
Такая настройка в большинстве случаев удовлетворяет требованиям по быстродействию и перерегулированию. Если объект регулирования содержит два инерционных звена с постоянными времени 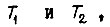 то передаточную функцию
то передаточную функцию 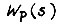 выбирают в виде
выбирают в виде
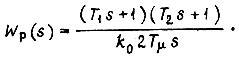
Благодаря наличию в составе регулятора интегрирующего элемента контур регулирования является системой астатической как по управляющему, так и по возмущающему воздействию. Однако, если реакция оптимизированного контура на скачок управляющей
величины характеризуется только суммой малых постоянных времени, то реакция на скачок возмущающего воздействия 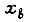 зависит также от других параметров контура. Максимальное отклонение регулируемой величины составляет
зависит также от других параметров контура. Максимальное отклонение регулируемой величины составляет 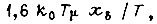 а время регулирования (достижение установившегося значения регулируемой величины) равно
а время регулирования (достижение установившегося значения регулируемой величины) равно 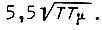
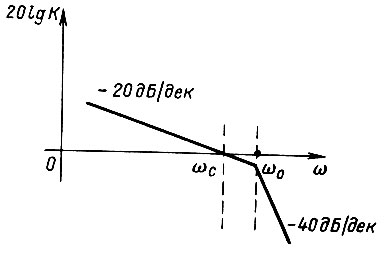
Рис. 34
Логарифмическая амплитудно-частотная характеристика оптимизированного по модульному критерию контура показа на рис. 34. В области низких и средних частот характеристика идет с наклоном -20 дБ/дек, а в области частот выше 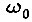 -40 дБ/дек. Запас по фазе составляет примерно 630. Частота среза
-40 дБ/дек. Запас по фазе составляет примерно 630. Частота среза 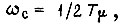 а частота сопряжения
а частота сопряжения 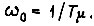
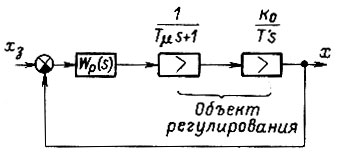
Рис. 35
Представим, что объект регулирования имеет передаточную функцию, показанную на рис. 35. Если выбрать для рассматриваемого контура регулятор с передаточной функцией
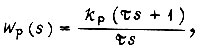
где 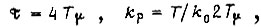 то передаточная функция замкнутого контура
то передаточная функция замкнутого контура 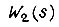 получит вид
получит вид
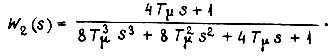
Здесь 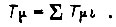 Замкнутый контур будет вести себя как система третьего порядка, его логарифмическая амплитудная частотная характеристика изображена на рис. 36. Характеристика симметрична относительно точки ее пересечения с осью частот, а частоты сопряжений вдвое меньше и вдвое больше частоты среза ωc Такой способ настройки получил название симметричного оптимума. В этом случае перерегулирование составляет примерно 43%, время первого достижения установившегося значения
Замкнутый контур будет вести себя как система третьего порядка, его логарифмическая амплитудная частотная характеристика изображена на рис. 36. Характеристика симметрична относительно точки ее пересечения с осью частот, а частоты сопряжений вдвое меньше и вдвое больше частоты среза ωc Такой способ настройки получил название симметричного оптимума. В этом случае перерегулирование составляет примерно 43%, время первого достижения установившегося значения 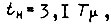 время окончательного достижения установившегося значения
время окончательного достижения установившегося значения 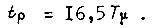 Величина перерегулирования уменьшается до 8% после установки в канале задания фильтра (рис. 37). Постоянная времени фильтра
Величина перерегулирования уменьшается до 8% после установки в канале задания фильтра (рис. 37). Постоянная времени фильтра 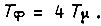 Получаем
Получаем 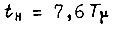 и
и 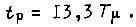
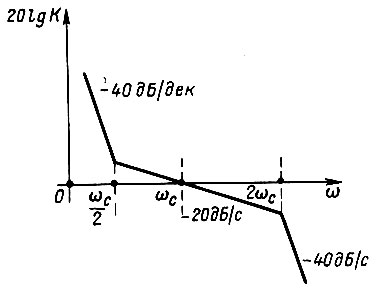
Рис. 36
В результате выбора ИП-регулятора для настройки контура, содержащего интегрирующее звейо в объекте регулирования, получается двукратно интегрирующая система, характеризующаяся высоким быстродействием при отработке возмущений и отсутствием статической ошибки. Настройку контура по симметричному оптимуму можно также применить, если объект регулирования содержит не интегрирующее, а инерционное звено с постоянной времени 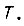 Желаемую настройку получаем при
Желаемую настройку получаем при 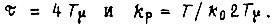 При
При 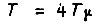 такая настройка совпадает с настройкой по модульному оптимуму, а при
такая настройка совпадает с настройкой по модульному оптимуму, а при 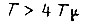 и наличии фильтра в канале задания качество регулирования будет выше, чем при настройке по модульному оптимуму.
и наличии фильтра в канале задания качество регулирования будет выше, чем при настройке по модульному оптимуму.
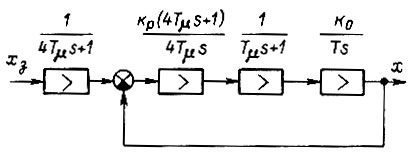
Рис. 37
В системах электропривода с последовательной коррекцией в качестве контурных регуляторов применяют операционные усилители.
В системе электропривода с подчиненным регулированием, во внешнем контуре которого происходит регулирование пути, проходимого двигателем, целесообразно использовать квадратичную обратную связь по скорости. Такая связь способствует получению минимального времени обработки заданных перемещений. Узел квадратичной обратной связи может быть выполнен в виде нелинейного элемента с параболической характеристикой, на вход которого подается сигнал, пропорциональной скорости. Этот узел может быть также выполнен как множительное устройство, состоящее из двух тахогенераторов. Напряжение на якоре одного из них является напряжением возбуждения второго.
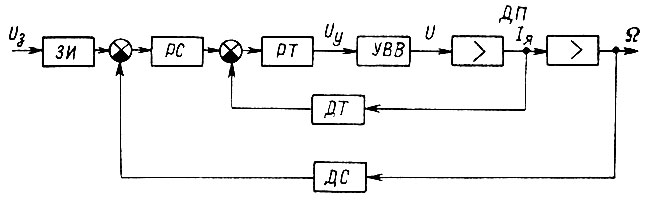
Рис. 38
При реализации последовательной коррекции в системе тириоторного электропривода вводят два контура по методу подчиненного регулирования (не считая связи по пути): по току якоря двигателя и по скорости вращения. Такая система показана на рис. 38. Здесь РТ - регулятор тока, PC - регулятор скорости, ДП - исполнительный двигатель постоянного тока, УВВ - управляемый вентильный выпрямитель, ДТ - датчик тока, ДС - датчик скорости, ЗИ - задатчик интенсивности пуска и#торможения.
Нелинейность параметров объектов регулирования робота внутри подчиненных контуров позволяет применить теорию линейного синтеза только при условии, что на каждом малом отрезке времени 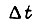 параметры корректирующих звеньев с передаточными функциями
параметры корректирующих звеньев с передаточными функциями 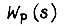 устанавливаются заново с целью получения одной и той же динамики САР.
устанавливаются заново с целью получения одной и той же динамики САР.
Заметим, что контур пути целесообразно синтезировать вариационным методом, пренебрегая инерционностью контура тока. Для позиционного привода критерием синтеза являются быстродействие, нагрев двигателя, расход энергии и т. д. Следящий привод характеризуется основным желаемым свойством - малой ошибкой слежения,которая выше относилась к 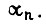 Метод подчиненного регулирования применим также к приводам переменного тока, у которых внутренним контуром в этом случае является контур частотно-токового управления.
Метод подчиненного регулирования применим также к приводам переменного тока, у которых внутренним контуром в этом случае является контур частотно-токового управления.
Определим добавочное управление, целью которого является компенсация волновых упругих колебаний звена робота. Запишем уравнение равновесия приращений сил на выходном валу привода:
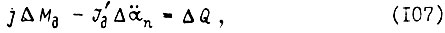
приращение момента двигателя 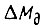 обеспечивается добавочным управлением;
обеспечивается добавочным управлением; 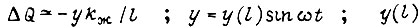 - амплитуда колебаний изгиба (21) при
- амплитуда колебаний изгиба (21) при 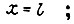 отношение
отношение 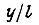 принимается приближенно за угол поворота свободного конца звена по отношению к концу, соединенному с валом привода, появившийся из-за волновых упругих колебаний изгиба звена;
принимается приближенно за угол поворота свободного конца звена по отношению к концу, соединенному с валом привода, появившийся из-за волновых упругих колебаний изгиба звена; 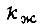 - коэффициент жесткости звена.
- коэффициент жесткости звена.
Подставим выражение (9) в уравнение (107):
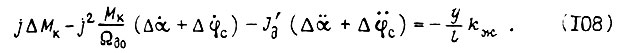
Приращение изгиба 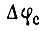 равно
равно 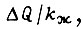 т. е.
т. е. 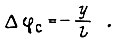 Пусть
Пусть 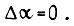 Тогда для двигателя постоянного тока, у которого
Тогда для двигателя постоянного тока, у которого 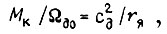 получаем из уравнения (108)
получаем из уравнения (108)
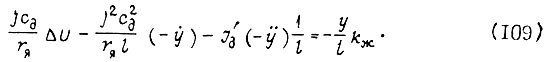
Отсюда приращение напряжения на якоре двигателя
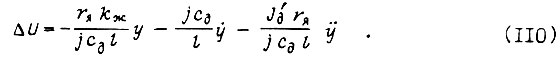
Если на свободном конце звена рабочего органа установлен акселерометр, с помощью которого измеряется 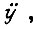 то управление
то управление 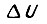 реализуем с помощью двух интеграторов и сумматора. Однако акселерометр измеряет вместо
реализуем с помощью двух интеграторов и сумматора. Однако акселерометр измеряет вместо 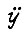 сумму
сумму 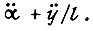 Поэтому линейный синтез исполнительной системы робота для i-й степени свободно должен проводиться с учетом контура обратной связи по ускорению свободного конца звена
Поэтому линейный синтез исполнительной системы робота для i-й степени свободно должен проводиться с учетом контура обратной связи по ускорению свободного конца звена 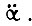 Этот контур неизбежно появляется в случае компенсации упругих волновых колебаний звена с помощью управления
Этот контур неизбежно появляется в случае компенсации упругих волновых колебаний звена с помощью управления 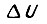 в соответствии с формулой (110). Для привода переменного тока вместо
в соответствии с формулой (110). Для привода переменного тока вместо 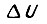 рассматривается приращение частоты
рассматривается приращение частоты 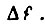
Например, из (54) при 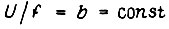
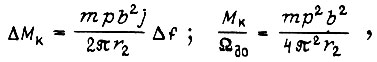
тогда,
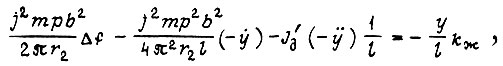
откуда приращение частоты напряжения на статоре асинхронного двигателя, компенсирующее колебания свободного конца звена рабочего органа:
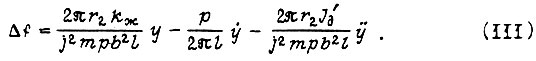
Особым вопросом является вопрос синтеза контуров виброзащиты манипулятора, установленного на вибрирующем основании. Здесь применима известная теория систем активной виброзащиты, основанная на методах оптимального управления.
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'