
5. Применение вариационного метода
Рассмотрим вариационный метод синтеза управлений двигателями на примере электроприводов.
Электроприводы можно разделить на две группы: приводы, в которых определяющими являются ограничения по нагреву и энергии, и приводы, в которых существенными являются только ограничения по току, скорости вращения, напряжению и т. п. Первой группе соответствует длительный режим работы или повторно-кратковременный с большой частотой включений, второй - кратковременный или повторно-кратковременный с длительными паузами между рабочими циклами. Законы оптимального управления для приводов первой группы обычно определяются на основе классического вариационного исчисления и реализуются регуляторами непрерывного действия.
Уравнение равновесия моментов на 1валу электродвигателя постоянного тока при неизменном моменте инерции и моменте сопротивления имеет вид
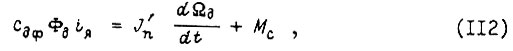
где 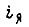 - ток якоря;
- ток якоря; 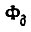 - результирующий магнитный поток;
- результирующий магнитный поток; 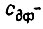 конструктивный коэффициент;
конструктивный коэффициент; 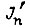 - момент инерции привода, приведенный к валу двигателя;
- момент инерции привода, приведенный к валу двигателя; 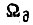 - угловая скорость;
- угловая скорость; 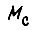 - момент сопротивления исполнительного механизма; t - время. Здесь
- момент сопротивления исполнительного механизма; t - время. Здесь 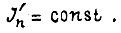 Обозначим
Обозначим 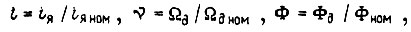
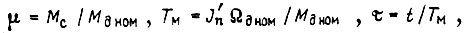 где
где 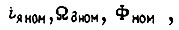
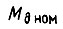 - номинальные величины. Тогда из (112) получаем в относительных единицах
- номинальные величины. Тогда из (112) получаем в относительных единицах

Если 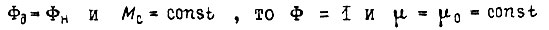

Приняв за единицу количества тепла, выделяющегося в меди якоря, тепло, выделяющееся в номинальном режиме за время 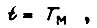 определяем тепло для времени
определяем тепло для времени 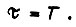
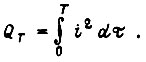
В длительном режиме 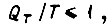 в кратковременном и повторно-кратковременном режиме допустимо
в кратковременном и повторно-кратковременном режиме допустимо 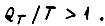 Если за единицу перегрева меди якоря над температурой охлаждающего воздуха принять перегрев в номинальном режиме, то нагрев меди можно описать уравнением
Если за единицу перегрева меди якоря над температурой охлаждающего воздуха принять перегрев в номинальном режиме, то нагрев меди можно описать уравнением
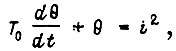
где 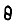 - превышение температуры меди якоря над температурой воздуха в относительных единицах;
- превышение температуры меди якоря над температурой воздуха в относительных единицах; 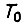 - постоянная времени нагрева. Обычно
- постоянная времени нагрева. Обычно 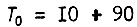
Напряжение на зажимах якоря в относительных единицах

где 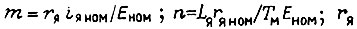 - активное сопротивление якорной цепи,
- активное сопротивление якорной цепи, 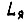 - индуктивность,
- индуктивность, 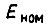 - э. д. с. вращения в номинальном режиме. Напряжение U отнесено к величине
- э. д. с. вращения в номинальном режиме. Напряжение U отнесено к величине 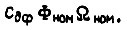 Пусть вал электропривода, описываемого уравнением (114), перемещается на отрезке времени τ от 0 до T на угол α при нулевых начальной и конечной скоростях вращения
Пусть вал электропривода, описываемого уравнением (114), перемещается на отрезке времени τ от 0 до T на угол α при нулевых начальной и конечной скоростях вращения 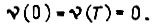 Затем следует пауза длительностью
Затем следует пауза длительностью 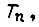 , после чего имеет новый цикл, и т. д. для того чтобы не происходило перегрева электродвигателя, должно выполняться неравенство
, после чего имеет новый цикл, и т. д. для того чтобы не происходило перегрева электродвигателя, должно выполняться неравенство
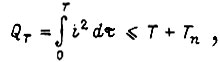
означающее, что количество тепла, которое выделяется в обмотке якоря за время работы T, не превосходит количество тепла, которое может быть отведено охлаждающим воздухом без превышения номинального перегрева обмоток за полное время цикла 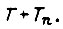 При полном использовании двигателя по нагреву неравенство для
При полном использовании двигателя по нагреву неравенство для 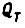 переходит в равенство. Задача нахождения оптимального движения привода формулируется так: найти функции
переходит в равенство. Задача нахождения оптимального движения привода формулируется так: найти функции 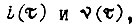 доставляющие максимум
доставляющие максимум 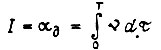 при заданном значении интеграла
при заданном значении интеграла 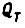 и уравнении связи (114). Ограничения величин тока i и скорости v отсутствуют.
и уравнении связи (114). Ограничения величин тока i и скорости v отсутствуют.
Составляем функционал
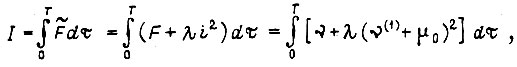
где 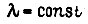 - неопределенный множитель Лагранжа.
- неопределенный множитель Лагранжа.
Запишем уравнение Эйлера
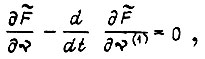
т. е. 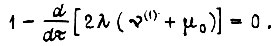 Отсюда
Отсюда 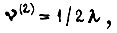
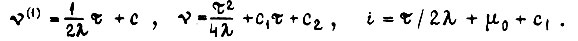 Поскольку
Поскольку 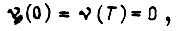 то
то 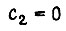 и
и 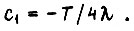 Тогда
Тогда 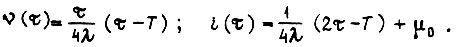
Величину λ находим из условия
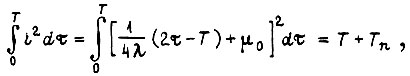
откуда 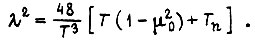 Максимуму
Максимуму 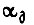 соответствует условие
соответствует условие 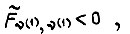 где
где 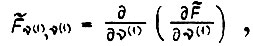 т. е.
т. е. 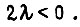 Поэтому
Поэтому 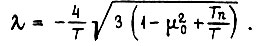 Тогда получаем оптимальные функции
Тогда получаем оптимальные функции 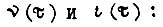
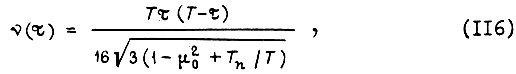
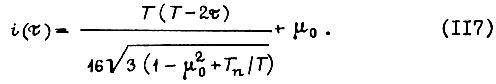
Проинтегрировав (116) от 0 до T, находим угол поворота вала электродвигателя
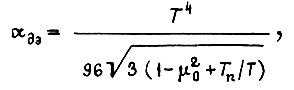
откуда
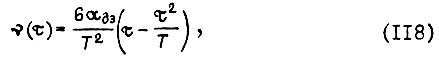
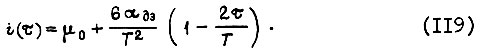
На рис. 39 б показан вид диаграмм тока и скорости двигателя для оптимального переходного процесса, несколько отличающихся от (118) и (119). От линейной диаграммы (119) необходимо отказаться в том случае, когда максимальное значение тока якоря 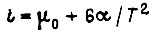 больше, чем значение
больше, чем значение 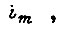 допустимое по условиям коммутации. Наилучшей тогда является смешанная диаграмма, составленная из участков
допустимое по условиям коммутации. Наилучшей тогда является смешанная диаграмма, составленная из участков 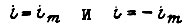 и линейного участка между ними (рис. 39 б). В работе [18] приведены соотношения параметров смешанной диаграммы:
и линейного участка между ними (рис. 39 б). В работе [18] приведены соотношения параметров смешанной диаграммы:
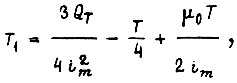
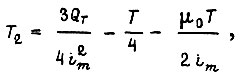
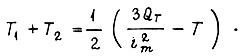
При 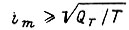 получаем вырожденные диаграммы тока и скорости, изображенные на рис. 39 в. Они оптимальны для электродвигателей с длительностью пауз во много раз большей длительности работы (более чем в 8 раз) и для кратковременной работы. Параметры вырожденных диаграмм могут быть получены с использованием принципа максимума. Заметим, что ни линейная, ни вырожденная диаграммы тока не могут быть точно реализованы, поскольку цепь якоря электродвигателя обладает индуктивностью.
получаем вырожденные диаграммы тока и скорости, изображенные на рис. 39 в. Они оптимальны для электродвигателей с длительностью пауз во много раз большей длительности работы (более чем в 8 раз) и для кратковременной работы. Параметры вырожденных диаграмм могут быть получены с использованием принципа максимума. Заметим, что ни линейная, ни вырожденная диаграммы тока не могут быть точно реализованы, поскольку цепь якоря электродвигателя обладает индуктивностью.
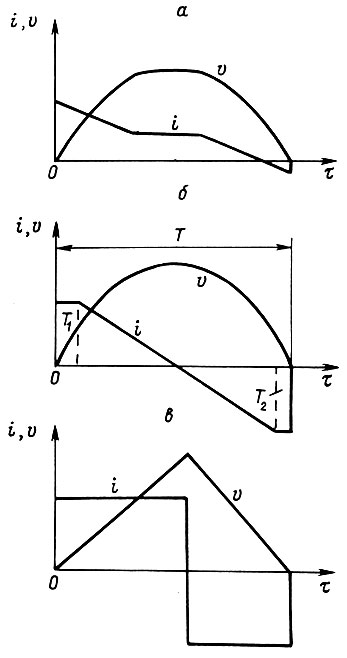
Рис. 39
Теперь найдем оптимальные диаграммы тока 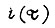 и скорости
и скорости 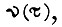 для которых принимает минимальное значение интеграл
для которых принимает минимальное значение интеграл 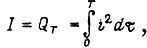 если заданы условия
если заданы условия 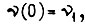
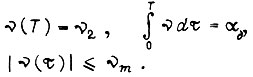
Составляем функционал
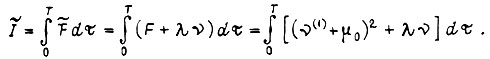
Приходим к уравнению Эйлера 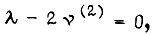 т. е.
т. е. 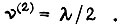 Тогда
Тогда 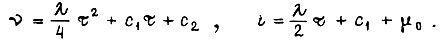 Воспользуемся граничными условиями:
Воспользуемся граничными условиями:
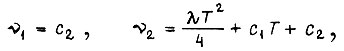
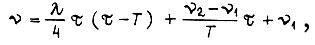
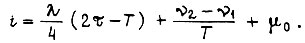
Для нахождения множителя Лагранжа λ интегрируем функцию 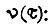
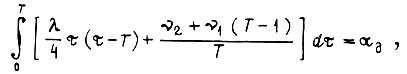
откуда 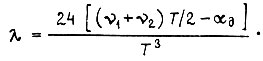
Подставляем λ в формулы скорости и тока:
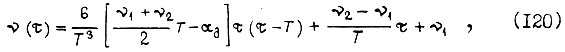
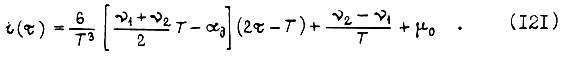
Если 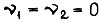 то выражение (120) совпадает с (118), а (121) с (119). Формула (120) может быть использована в том случае, когда максимальная ордината диаграммы скорости не превышает по абсолютной величине
то выражение (120) совпадает с (118), а (121) с (119). Формула (120) может быть использована в том случае, когда максимальная ордината диаграммы скорости не превышает по абсолютной величине 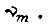 При превышении же экстремум I достигается на диаграмме скорости, составленной из отрезков экстремали и участка постоянной скорости
При превышении же экстремум I достигается на диаграмме скорости, составленной из отрезков экстремали и участка постоянной скорости 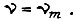 Известно, что в точках сопряжения экстремали
Известно, что в точках сопряжения экстремали 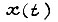 и граничной кривой
и граничной кривой 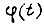 касательные к ним должны совпадать, т. е.
касательные к ним должны совпадать, т. е. 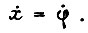 В решаемой задаче оптимальную диаграмму скорости находим из условий
В решаемой задаче оптимальную диаграмму скорости находим из условий 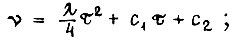 на первом участке
на первом участке 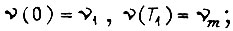 на третьем участке
на третьем участке 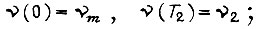 на втором участке
на втором участке 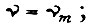
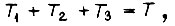 где
где 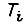 - длительность
- длительность 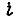 -го участка;
-го участка; 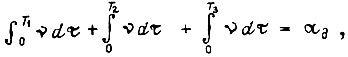 где время считается с нуля от начала каждого отрезка; ускорение в конце первого участка
где время считается с нуля от начала каждого отрезка; ускорение в конце первого участка 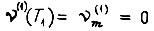 и аналогично ускорение в начале третьего участка
и аналогично ускорение в начале третьего участка 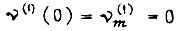
На рис. 39 а показаны оптимальные диаграммы скорости и тока при наличии локального ограничения 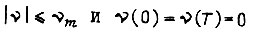 Если максимальный ток на диаграмме
Если максимальный ток на диаграмме 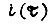 превышает допустимое значение
превышает допустимое значение 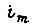 по абсолютной величине, то оптимальная диаграмма тока составляется из участков границы области
по абсолютной величине, то оптимальная диаграмма тока составляется из участков границы области 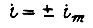 и участка, соответствующего экстремали
и участка, соответствующего экстремали 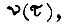 либо диаграмма является вырожденной. Появление в кривой тока участков
либо диаграмма является вырожденной. Появление в кривой тока участков 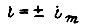 означает появление функций
означает появление функций 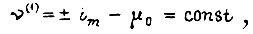 что приводит к необходимости скорректировать диаграмму скорости на этих участках, полученную без учета ограничения
что приводит к необходимости скорректировать диаграмму скорости на этих участках, полученную без учета ограничения 
Если в задачу системы электропривода входит только требуемое изменение скорости 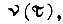 обеспечивающее минимум интеграла
обеспечивающее минимум интеграла
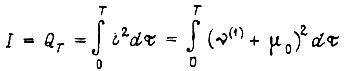
при заданных граничных условиях 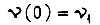 и
и 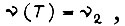 то уравнение Эйлера принимает вид
то уравнение Эйлера принимает вид 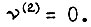 Тогда
Тогда 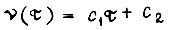 где
где 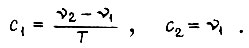 Ток в якоре изменяется по закону
Ток в якоре изменяется по закону 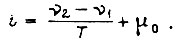 Напряжение на зажимах якоря должно возрастать по линейному закону в функции времени:
Напряжение на зажимах якоря должно возрастать по линейному закону в функции времени:
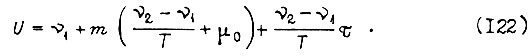
Формула (122) получена при 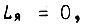 т. е. n = 0 в соответствии с равенством (115). В работе [18] учитывается зависимость теплоотдачи от температуры меди якоря с помощью уравнения
т. е. n = 0 в соответствии с равенством (115). В работе [18] учитывается зависимость теплоотдачи от температуры меди якоря с помощью уравнения 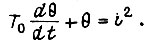
Решим следующую задачу. Найти функции 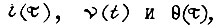 обеспечивающие наибольшее изменение скорости вращения вала двигателя в заданное время T при учете уравнений связи
обеспечивающие наибольшее изменение скорости вращения вала двигателя в заданное время T при учете уравнений связи 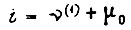 и
и 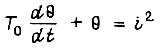 и ограничения по температуре изоляции
и ограничения по температуре изоляции 
Второе уравнение связи запишем в виде
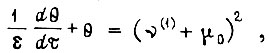
где 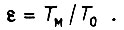 Исходя из максимизации приращения
Исходя из максимизации приращения 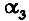 составляем функционал
составляем функционал
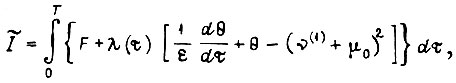
где 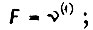
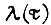 - множитель Лагранжа.
- множитель Лагранжа.
Уравнение Эйлера для функции 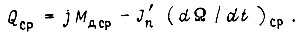
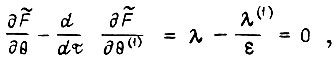
из которого определяем 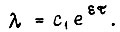
Уравнение Эйлера для функции 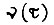
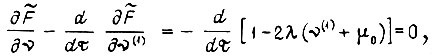
откуда 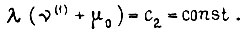 Тогда ток изменяется по закону
Тогда ток изменяется по закону 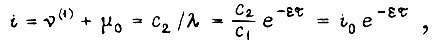 где
где 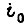 - ток якоря в начальный момент времени
- ток якоря в начальный момент времени 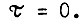
Скорость вращения вала двигателя 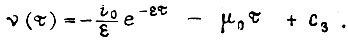 Для заданного начального условия
Для заданного начального условия 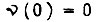
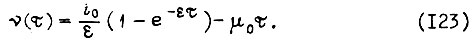
Из второго уравнения связи для 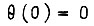
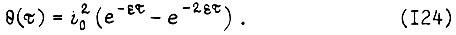
Кривая θ(τ) имеет максимальное значение, равное 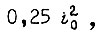 которому соответствует
которому соответствует 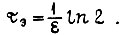 Если
Если 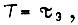 то из условия
то из условия 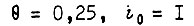 получаем
получаем 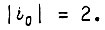 Для меньших значений T, т. е. для
Для меньших значений T, т. е. для  начальный ток равен
начальный ток равен 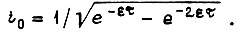
Если же  то максимальное приращение скорости
то максимальное приращение скорости 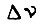 за переходный процесс достигается на кривой
за переходный процесс достигается на кривой 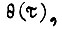 составленной из экстремали и участка границы области
составленной из экстремали и участка границы области 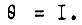 В точках сопряжения касательные к экстремали и к границе области должны совпадать, если
В точках сопряжения касательные к экстремали и к границе области должны совпадать, если 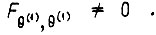 В данной задаче функционал
В данной задаче функционал 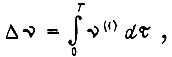 с помощью уравнения
с помощью уравнения 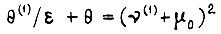 приводится к виду
приводится к виду
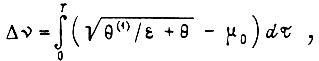
откуда
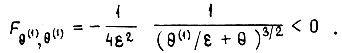
Выше рассмотрены оптимальные движения приводов с электродвигателями, у которых относительное значение потока 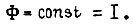 Если поток непостоянен, то из уравнения (113) имеем
Если поток непостоянен, то из уравнения (113) имеем 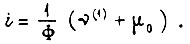 Тогда
Тогда 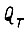 равно
равно
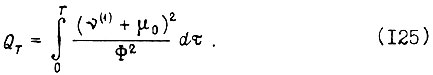
Если требуется найти оптимальные функции 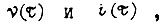 доставляющие минимум
доставляющие минимум 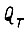 при заданном значении
при заданном значении 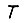 и приращении угла поворота вала привода
и приращении угла поворота вала привода 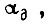 причем
причем 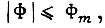 то приходим к изопериметрической задаче со вспомогательным функционалом
то приходим к изопериметрической задаче со вспомогательным функционалом
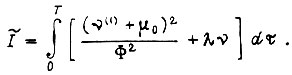
Записав уравнение Эйлера для функции 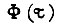
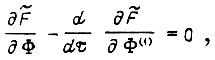
получаем
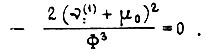
В данном случае экстремалей не существует для любой допускаемой функции 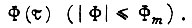 Экстремум
Экстремум 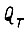 имеем на границе области значений потока при
имеем на границе области значений потока при 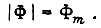 Магнитный поток следует поддерживать постоянным и равным своему максимальному значению. Исключением являются лишь те случаи, когда существенно ограничение по напряжению [18].
Магнитный поток следует поддерживать постоянным и равным своему максимальному значению. Исключением являются лишь те случаи, когда существенно ограничение по напряжению [18].
Наряду с интегральными критериями качества переходных процессов в системах привода, характеризующими их производительность либо нагрев двигателей, пользуются функционалами, описывающими длительность процесса или энергию, затрачиваемую для перемещения. Определение наименьшего времени 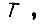 за которое вал привода поворачивается на угол
за которое вал привода поворачивается на угол 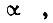 связано с нахождением функций
связано с нахождением функций 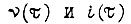 минимизирующих интеграл
минимизирующих интеграл 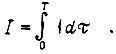 Энергия же, потребляемая из сети, равна
Энергия же, потребляемая из сети, равна
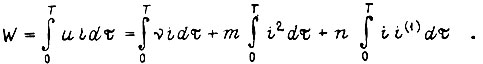
Первая составляющая
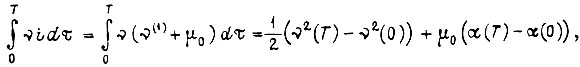
третья составляющая
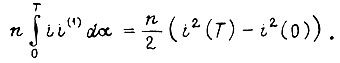
Обычно от управления зависит только вторая составляющая
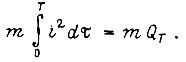
Следовательно, при постоянных моменте сопротивления 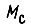 и моменте инерции J законы управления, обеспечивающие минимум нагрева якоря и минимум потребления энергии, совпадут.
и моменте инерции J законы управления, обеспечивающие минимум нагрева якоря и минимум потребления энергии, совпадут.
При моменте сопротивления на валу, линейно зависящем от скорости, минимизация энергии, потребляемой электродвигателем для осуществления заданного перемещения механизма, сводится к нахождению условий, доставляющих экстремум интегралу
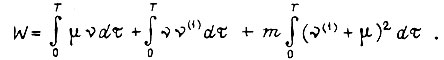
Вторая составляющая не зависит от функции 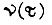 и целиком определяется заданием
и целиком определяется заданием 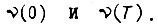 Поэтому при заданном значении пути
Поэтому при заданном значении пути 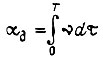 подынтегральная функция функционала
подынтегральная функция функционала 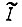 есть
есть
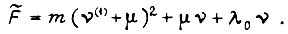
Уравнение Эйлера для 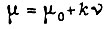 принимает вид
принимает вид
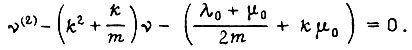
Его решение: 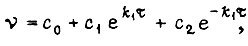 где
где 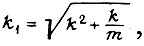 т. е. критерии минимума потребляемой энергии и минимума потерь в якоре не совпадают.
т. е. критерии минимума потребляемой энергии и минимума потерь в якоре не совпадают.
Рассмотрим управление асинхронным двигателем. В большинстве случаев оптимальное управление асинхронным двигателем в смысле производительности и быстродействия определяется ограничениями по нагреву. В электроприводах же постоянного тока, особенно в кратковременном режиме работы, производительность и быстродействие чаще ограничены условиями коммутации. Прежде чем сформулировать задачу об оптимальном частотном управлении асинхронным двигателем, доставляющим экстремум нагреву двигателя, сделаем следующие допущения. Не будем учитывать электромагнитные переходные процессы. За единицу магнитного потока, сцепленного с ротором, примем 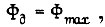 т. е. максимальный поток, возможный с учетом насыщения стали. Практически
т. е. максимальный поток, возможный с учетом насыщения стали. Практически 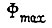 мало отличается от магнитного потока двигателя в номинальном режиме. За единицу скорости примем синхронную скорость вращения ротора (скольжение равно нулю) при частоте тока в статоре, равной номинальной. За единицу частоты тока в роторе примем такую частоту, при которой активное сопротивление ротора равно его реактивному сопротивлению, зависящему от частоты. За единицу электромагнитного момента двигателя примем критический момент, т. е. момент при магнитном потоке, равном максимальному, и частоте тока ротора, принятой за единицу. За единицу времени примем постоянную TM, численно равную времени разгона привода от нулевой до синхронной скорости при электромагнитном моменте, равном критическому. За единицу частоты тока статорной цепи примем номинальную частоту
мало отличается от магнитного потока двигателя в номинальном режиме. За единицу скорости примем синхронную скорость вращения ротора (скольжение равно нулю) при частоте тока в статоре, равной номинальной. За единицу частоты тока в роторе примем такую частоту, при которой активное сопротивление ротора равно его реактивному сопротивлению, зависящему от частоты. За единицу электромагнитного момента двигателя примем критический момент, т. е. момент при магнитном потоке, равном максимальному, и частоте тока ротора, принятой за единицу. За единицу времени примем постоянную TM, численно равную времени разгона привода от нулевой до синхронной скорости при электромагнитном моменте, равном критическому. За единицу частоты тока статорной цепи примем номинальную частоту 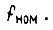 За единицу тока в роторе - ток при частоте, принятой за единицу, и
За единицу тока в роторе - ток при частоте, принятой за единицу, и 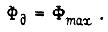
Электромагнитный момент двигателя запишем в виде [18]
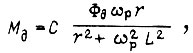
где 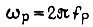 - круговая частота тока ротора;
- круговая частота тока ротора; 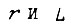 - активное сопротивление фазы ротора и индуктивность; c = const.
- активное сопротивление фазы ротора и индуктивность; c = const.
Если при частоте 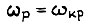 имеем
имеем 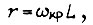 то момент, равный критическому:
то момент, равный критическому:
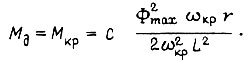
Введя обозначения
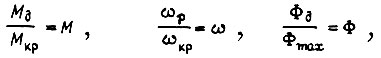
получаем выражение момента двигателя в относительных единицах:
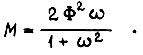
В относительных единицах будем учитывать также угловую скорость вращения вала 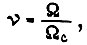 момент сопротивления
момент сопротивления 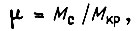 время
время 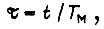 частоту статора
частоту статора 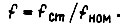 Здесь
Здесь 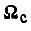 - угловая синхронная скорость вращения вала.
- угловая синхронная скорость вращения вала.
Если количество тепла, выделившееся в роторе за время  при токе, соответствующем
при токе, соответствующем 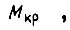 принять за единицу, то в относительных единицах количество тепла, выделившееся в роторе за время
принять за единицу, то в относительных единицах количество тепла, выделившееся в роторе за время 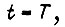 равно интегралу
равно интегралу
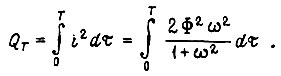
Уравнение равновесия моментов сил на валу

Сформулируем задачу оптимального частотного управления двигателем: найти функции 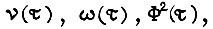 доставляющие минимум интегралу
доставляющие минимум интегралу 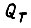 при заданных значении
при заданных значении 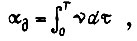 уравнении равновесия моментов сил на валу, неравенстве
уравнении равновесия моментов сил на валу, неравенстве 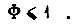 Учет ограничений, накладываемых на координаты
Учет ограничений, накладываемых на координаты 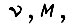 может быть произведен после решения поставленной задачи аналогично рассмотренному выше составлению скорректированных диаграмм двигателя постоянного тока.
может быть произведен после решения поставленной задачи аналогично рассмотренному выше составлению скорректированных диаграмм двигателя постоянного тока.
Составляем функционал 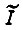 для нахождения уравнений Эйлера
для нахождения уравнений Эйлера
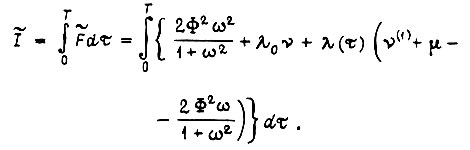
Пусть 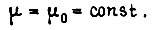 Варьируя
Варьируя 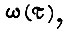 приходим к уравнению
приходим к уравнению

Уравнение Эйлера для функции 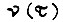

Наконец, для функции 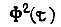 получаем
получаем
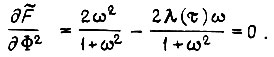
Подставив уравнение (127) в (129), приходим к формуле

За исключением тривиального случая, когда 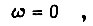 т. е.
т. е. 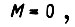 производная
производная 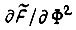 не обращается в нуль. При
не обращается в нуль. При 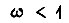 она отрицательна, т. е. потери в роторе при выполнении заданного перемещения тем меньше, чем больше магнитный поток, и минимум потерь достигается на границе области
она отрицательна, т. е. потери в роторе при выполнении заданного перемещения тем меньше, чем больше магнитный поток, и минимум потерь достигается на границе области 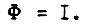 Режим, в котором
Режим, в котором 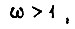 неоптимален. Напряжение на зажимах двигателя с короткозамкнутым ротором следует регулировать так, чтобы магнитный поток, сцепленный с ротором, оставался постоянным и максимальным, соответствуя насыщению стали. Из уравнений (127) и (128)
неоптимален. Напряжение на зажимах двигателя с короткозамкнутым ротором следует регулировать так, чтобы магнитный поток, сцепленный с ротором, оставался постоянным и максимальным, соответствуя насыщению стали. Из уравнений (127) и (128)
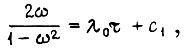
откуда
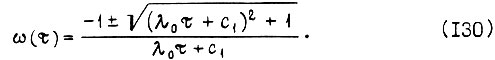
Из уравнения (126) находим скорость вращения
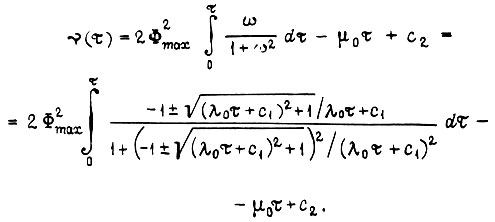
Рассмотренное выше оптимальное управление электродвигателями постоянного и переменного токов относится к случаю, когда момент инерции привода, приведенный к валу двигателя, и момент сопротивления неизменны (либо 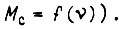 ). Если в микропроцессор, управляющий приводами робота, на каждом малом отрезке времени
). Если в микропроцессор, управляющий приводами робота, на каждом малом отрезке времени 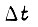 поступают измеренные или вычисленные значения
поступают измеренные или вычисленные значения 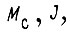 то производится пересчет коэффициентов экстремалей для новых
то производится пересчет коэффициентов экстремалей для новых 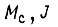 с учетом движения, уже совершенного приводом от начала рассматриваемого цикла. Для полученных скоростей
с учетом движения, уже совершенного приводом от начала рассматриваемого цикла. Для полученных скоростей 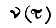 и тока
и тока 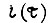 находится новое напряжение или частота на двигателе. В некоторых случаях можно получить движение в цикле, мало отличающееся от оптимального.
находится новое напряжение или частота на двигателе. В некоторых случаях можно получить движение в цикле, мало отличающееся от оптимального.
Рассмотрим один из частных подходов к синтезу управлений электродвигателями манипулятора, схема которого показана на рис. 7. Для отыскания позиционного управления двигателями, оптимального по быстродействию, представим формулы (3), (4), (5) в виде
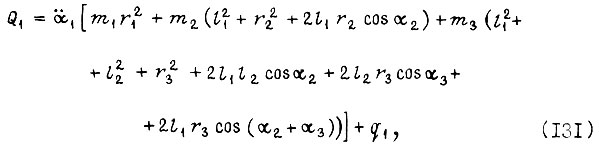
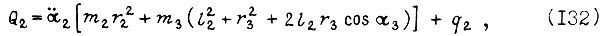

Рассмотрим движение звеньев на малом отрезке времени 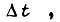 которому соответствуют приращения углов
которому соответствуют приращения углов 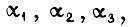 равные
равные 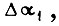 и практически постоянство функций
и практически постоянство функций 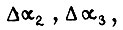
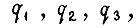 зависящих от углов поворота, скоростей и ускорений звеньев. Устремим к минимуму величину
зависящих от углов поворота, скоростей и ускорений звеньев. Устремим к минимуму величину 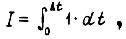 соблюдая условия
соблюдая условия
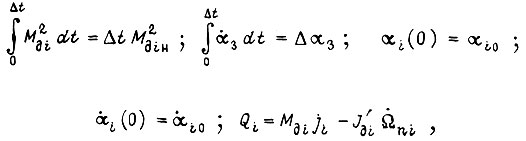
где 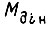 - заданный момент электродвигателя;
- заданный момент электродвигателя; 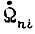 - ускорение вала привода; силы трения не учитываем.
- ускорение вала привода; силы трения не учитываем.
Для третьего двигателя минимизируем функционал
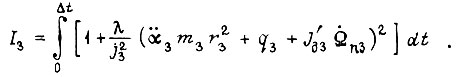
Из уравнения Эйлера - Пуассона
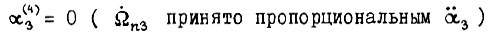
получаем 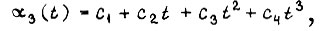 где
где 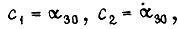
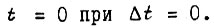 Ограничим приращения функций
Ограничим приращения функций 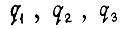 на отрезке
на отрезке 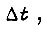 задав условие
задав условие 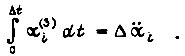 В условие нагрева подставим
В условие нагрева подставим 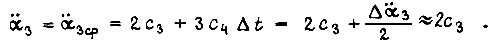 Тогда
Тогда
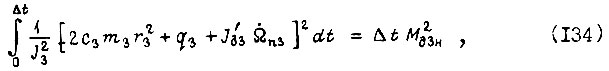
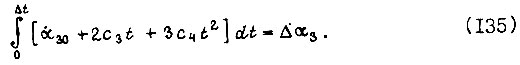
Принятое приближение для 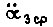 приемлемо, если считать, что
приемлемо, если считать, что 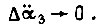 Из уравнений (134) и (135) получаем
Из уравнений (134) и (135) получаем
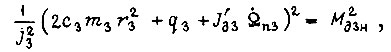
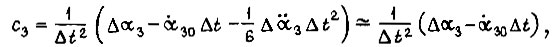
откуда определяются 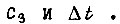 Итак, на отрезке времени
Итак, на отрезке времени 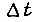 экстремаль
экстремаль
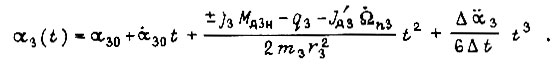
В момент времени
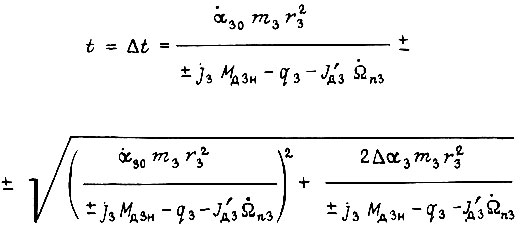
устройство, управляющее двигателем и силовым электронным преобразователем, вычисляет новые коэффициенты 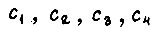 функции
функции 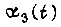 для следующего отрезка
для следующего отрезка 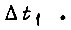 Здесь из двух разных знаков перед квадратным корнем следует брать тот, который соответствует наименьшему положительному значению
Здесь из двух разных знаков перед квадратным корнем следует брать тот, который соответствует наименьшему положительному значению 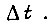 Знак перед
Знак перед 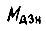 берется положительным или отрицательным в зависимости от того, согласно либо противоположно действуют моменты сил
берется положительным или отрицательным в зависимости от того, согласно либо противоположно действуют моменты сил 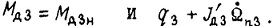
Для второго электродвигателя минимизируется функционал
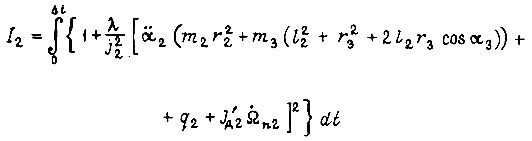
при соблюдении условий
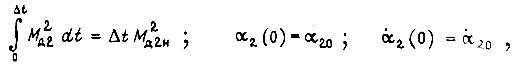
где 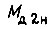 - заданный момент второго двигателя;
- заданный момент второго двигателя; 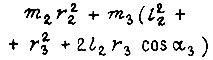 и
и 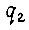 принимаются постоянными на отрезке
принимаются постоянными на отрезке 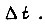
Оптимальная траектория второго звена есть 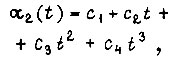 где
где 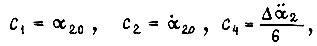 постоянная
постоянная 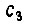 определяется из уравнения
определяется из уравнения
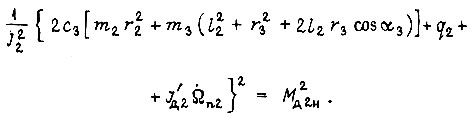
Постоянная 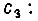
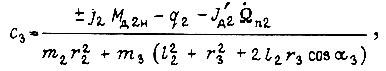
где знак перед 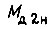 зависит от того, совпадают ли по направлению моменты сил
зависит от того, совпадают ли по направлению моменты сил 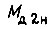 и
и 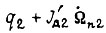 нет.
нет.
Для первого электродвигателя отыскиваем оптимальную траекторию 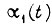 аналогично тому, как это выполнено для второго двигателя. В результате
аналогично тому, как это выполнено для второго двигателя. В результате
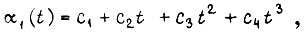
где 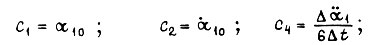
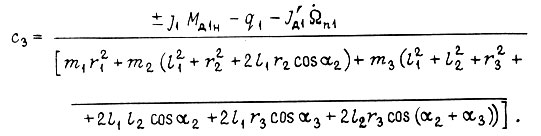
Перемещения первого и второго звеньев, совершаемые на отрезке 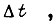 могут быть вычислены по формулам
могут быть вычислены по формулам
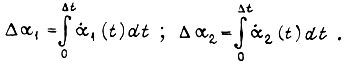
Если в вычислительном устройстве для некоторых отрезков времени из 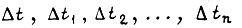 вычислительные значения скоростей и ускорений
вычислительные значения скоростей и ускорений 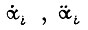 превышают допустимые величины из условий технологии и динамических перегрузок, то реализация предельно допустимых управлений не обеспечивает в этом случае полного использования электродвигателя по нагреву. При ограничении по ускорению в формуле
превышают допустимые величины из условий технологии и динамических перегрузок, то реализация предельно допустимых управлений не обеспечивает в этом случае полного использования электродвигателя по нагреву. При ограничении по ускорению в формуле 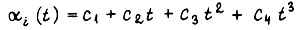 коэффициенты равны
коэффициенты равны 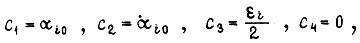 допустимое ускорение. При ограничении по скорости
допустимое ускорение. При ограничении по скорости 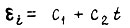 где
где 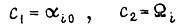 - допустимая скорость. Длительность отрезка
- допустимая скорость. Длительность отрезка 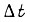 находим в первом случае из формулы
находим в первом случае из формулы 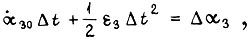 во втором
во втором 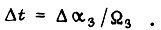
Заметим, что условие нагрева, использованное выше при синтезе движения, не учитывает теплоотдачи и относится к повторно-кратковременному режиму, когда нагрев обмотки двигателя не успевает приблизительно к допустимому за время цикла движения.
Для привода с двигателем постоянного тока независимого возбуждения находим управляющее напряжение на входе силового электронного преобразователя на отрезке времени 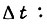
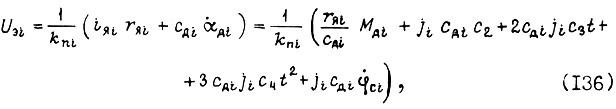
где ускорение и скорость не достигают ограничений; 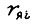 - сопротивление якорного контура двигателя;
- сопротивление якорного контура двигателя; 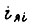 - ток якоря;
- ток якоря; 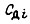 - конструктивный коэффициент двигателя;
- конструктивный коэффициент двигателя; 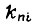 - коэффициент усиления преобразователя по напряжению;
- коэффициент усиления преобразователя по напряжению; 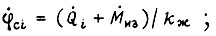 не учитывается влияние на переходный процесс индуктивного сопротивления якорной цепи.
не учитывается влияние на переходный процесс индуктивного сопротивления якорной цепи.
При достижении ограничения ускорения 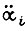
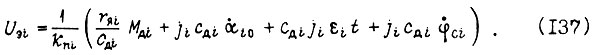
При ограничении скорости 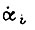
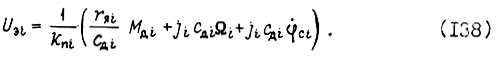
Управление в соответствии с формулами (136), (137), (138) получено без учета ограничения на величину напряжения 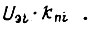
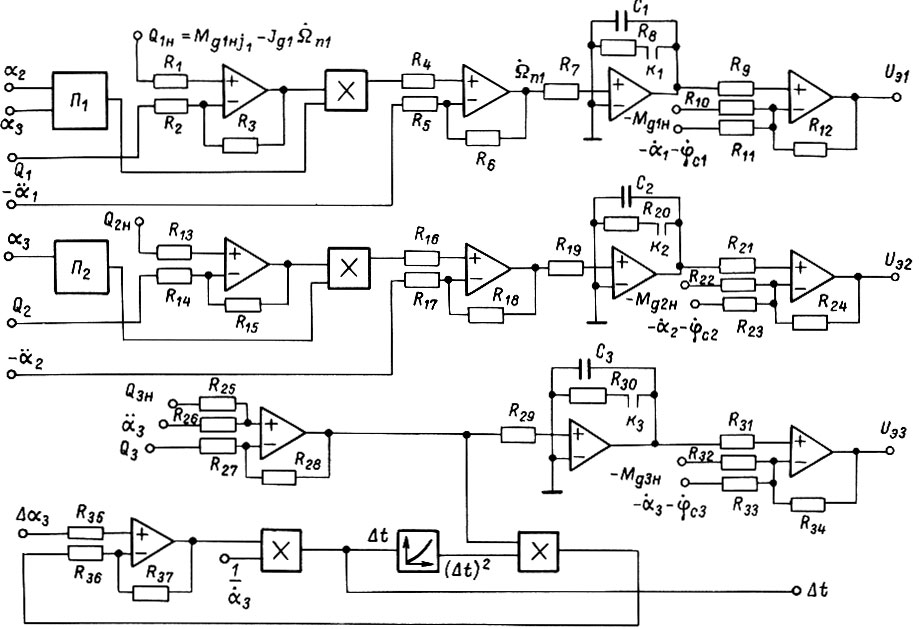
Рис. 40
На рис. 40 показана упрощенная схема, реализующая управление двигателями манипулятора по формуле (136) для 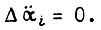 На входы схемы поступает информация о скоростях
На входы схемы поступает информация о скоростях 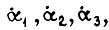 ускорениях
ускорениях 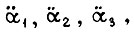 моментах сил
моментах сил 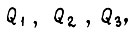 вычисленных или измеренных на прошлом малом отрезке времени и зафиксированных памятью внутри данного отрезка
вычисленных или измеренных на прошлом малом отрезке времени и зафиксированных памятью внутри данного отрезка 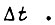 На основе этой информации вычисляются
На основе этой информации вычисляются 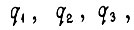 а затем управления для следующего отрезка, в начале которого на входы схемы поступают новые зафиксированные потенциалы; при этом нулевые значения сигналов на выходах интеграторов устанавливаются замыканием контуров разряда конденсаторов. На рис. 40 не показано вычисление
а затем управления для следующего отрезка, в начале которого на входы схемы поступают новые зафиксированные потенциалы; при этом нулевые значения сигналов на выходах интеграторов устанавливаются замыканием контуров разряда конденсаторов. На рис. 40 не показано вычисление 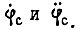 На выходе схемы имеем сигналы управления силовыми преобразователями
На выходе схемы имеем сигналы управления силовыми преобразователями 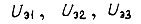 и потенциал, величина которого пропорциональна длительности малого отрезка
и потенциал, величина которого пропорциональна длительности малого отрезка 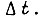 Сигнал на выходе преобразователя
Сигнал на выходе преобразователя 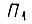 пропорционален величине
пропорционален величине
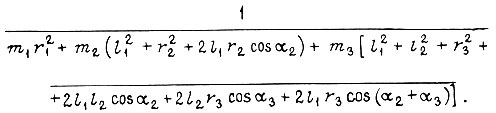
Сигнал на выходе преобразователя 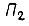 пропорционален величине
пропорционален величине
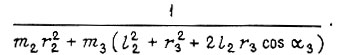
Управление, реализуемое схемой на рис. 40, отменяется программным устройством в начальной и конечной частях траектории руки, когда соблюдаются неравенства 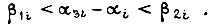 Это связано с требуемой плавностью трогания и остановки, здесь α3i - задание по перемещению i-го звена, ступенчато устанавливаемое во времени программным устройством.
Это связано с требуемой плавностью трогания и остановки, здесь α3i - задание по перемещению i-го звена, ступенчато устанавливаемое во времени программным устройством.
Синтез добавочного контура управления, компенсирующего волновые упругие колебания звена, может быть проведен с применением вариационного метода. В результате получаем новый закон приращения 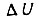 по сравнению с формулой (110). Основным подходом является синтез оптимальных траекторий
по сравнению с формулой (110). Основным подходом является синтез оптимальных траекторий 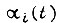 из условия ограничения энергии, переходящей в процесс генерирования упругих колебаний.
из условия ограничения энергии, переходящей в процесс генерирования упругих колебаний.
Для некоторых конструкций необщепромышленного назначения существенным является обеспечение такого управления в системах привода роботов, которому соответствуют удовлетворительно малые амплитуды волновых упругих колебаний звеньев в переходном процессе. При этом увеличение жесткости конструкции ограничено заданными весогабаритными показателями.
Разобьем ось времени t на малые отрезки 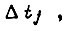 внутри каждого из которых имеют место заданные приращения углов поворота звеньев
внутри каждого из которых имеют место заданные приращения углов поворота звеньев 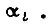 Примем, что робот обладает тремя степенями подвижности. Приращения
Примем, что робот обладает тремя степенями подвижности. Приращения 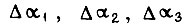 таковы, что в формулах вращающих моментов в шарнирах
таковы, что в формулах вращающих моментов в шарнирах 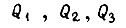 составляющие, зависящие от
составляющие, зависящие от 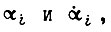 внутри
внутри 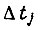 практически неизменны. Длительность переходного процесса
практически неизменны. Длительность переходного процесса 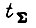 складывается из
складывается из 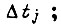
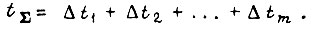 Задается функционал для i-го привода
Задается функционал для i-го привода
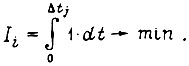
Принимаем, что амплитуда упругих колебаний не превысит некоторой величины, если приращение 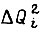 на
на 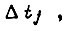 усредненное на этом отрезке, не превышает по абсолютной величине заданного приращения
усредненное на этом отрезке, не превышает по абсолютной величине заданного приращения 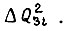 Это выражается условием
Это выражается условием
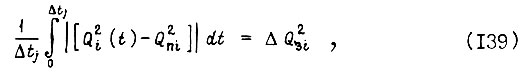
где 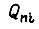 - вращающий момент
- вращающий момент 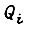 на предыдущем отрезке
на предыдущем отрезке 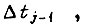 усредненный на этом отрезке. Упрощая решаемую задачу, исходим из предположения, что для всех
усредненный на этом отрезке. Упрощая решаемую задачу, исходим из предположения, что для всех 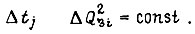 Эта величина гарантирует максимальную амплитуду упругих колебаний, определяемую по формуле (21).
Эта величина гарантирует максимальную амплитуду упругих колебаний, определяемую по формуле (21).
Задаются, кроме того, условия: 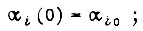
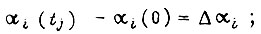
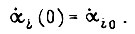 Здесь
Здесь 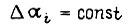 для всех
для всех 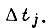 Время t в функционале и в изопериметрическом условии, записанных выше, отсчитывается от левого края отрезка
Время t в функционале и в изопериметрическом условии, записанных выше, отсчитывается от левого края отрезка 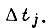
Составим вспомогательный функционал
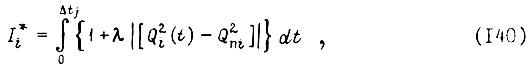
где λ - множитель Лагранжа.
Вращающие моменты сил 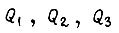 внутри
внутри 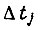 представим в виде
представим в виде
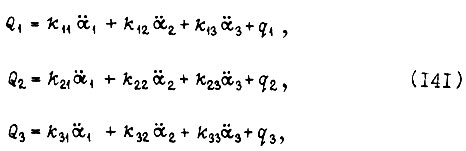
где коэффициенты 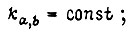 кроме того,
кроме того, 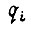 зависящие от углов поворота звеньев робота и скоростей, также постоянны. Для первого привода из функционала
зависящие от углов поворота звеньев робота и скоростей, также постоянны. Для первого привода из функционала
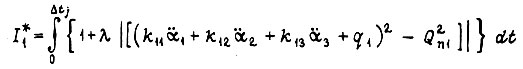
составляем уравнение Эйлера - Пуассона
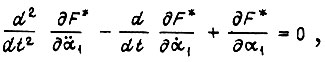
где 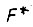 - подынтегральная функция
- подынтегральная функция 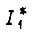 и получаем
и получаем
К этому же дифференциальному уравнению приходим, составив уравнение Эйлера - Пуассона для 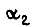 или
или 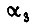 Рассмотрев функционалы
Рассмотрев функционалы 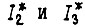 получаем систему дифференциальных уравнений
получаем систему дифференциальных уравнений
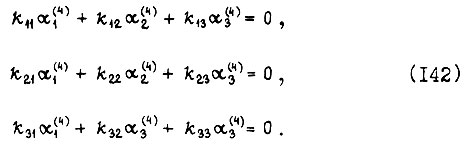
Приходим к выводу: 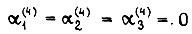 Воспользуемся одним из результатов:
Воспользуемся одним из результатов: 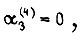 тогда
тогда
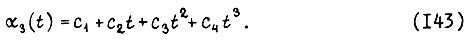
Пусть допускается скачкообразное изменение ускорений 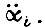 Тогда принимаем, что в системе привода управление внутри
Тогда принимаем, что в системе привода управление внутри 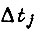 происходит так, что
происходит так, что 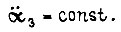 Это допущение упрощает реализацию управления. С учетом допущения
Это допущение упрощает реализацию управления. С учетом допущения 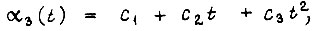 коэффициенты
коэффициенты 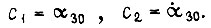 Подставив в
Подставив в 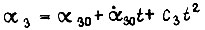 время -
время - 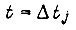 и
и 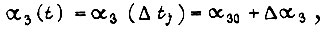 получаем
получаем
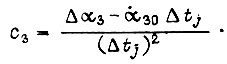
Итак, внутри 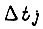
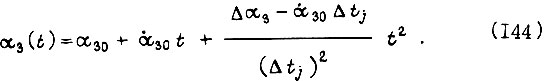
Для 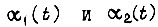 формулы аналогичны. Определим длину отрезка
формулы аналогичны. Определим длину отрезка 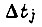 Весь путь, который должно пройти i-е звено робота в переходном процессе, разделим на две зоны. В первой зоне
Весь путь, который должно пройти i-е звено робота в переходном процессе, разделим на две зоны. В первой зоне 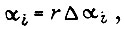 причем начальное значение
причем начальное значение 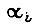 равно нулю;
равно нулю; 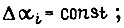 r - число отрезков
r - число отрезков 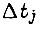 . В этой зоне
. В этой зоне 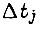 находим из условия:
находим из условия:
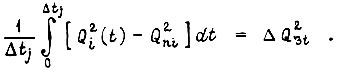
Во второй зоне также 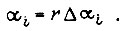 Величину
Величину 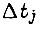 находим каждый раз из условия
находим каждый раз из условия
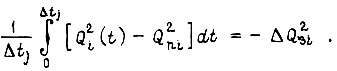
Тогда для первой зоны и третьего привода справедливо равенство
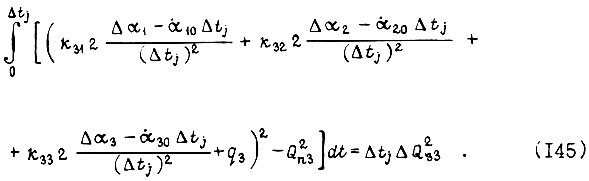
Длительность 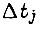 определяем из квадратного уравнения, соответствующего (145):
определяем из квадратного уравнения, соответствующего (145):
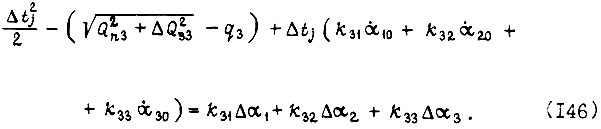
Во второй зоне вместо 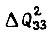 берем -
берем -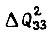 Из приращений
Из приращений 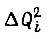 складывается максимальное значение
складывается максимальное значение 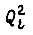 В переходном процессе, определяющее амплитуду упругих незатухающих колебаний
В переходном процессе, определяющее амплитуду упругих незатухающих колебаний 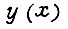 (см. гл. 1):
(см. гл. 1): 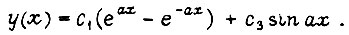 Знание оптимальных движений робота позволяет найти управления U3i на входах силовых преобразователей, соединенных с двигателями. Например, для электродвигателя постоянного тока независимого возбуждения
Знание оптимальных движений робота позволяет найти управления U3i на входах силовых преобразователей, соединенных с двигателями. Например, для электродвигателя постоянного тока независимого возбуждения
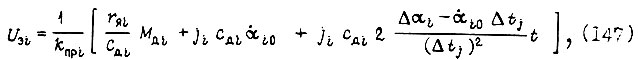
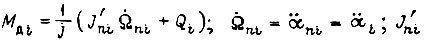
- момент инерции привода, приведенный к шарниру в данном случае постоянный).
Формулы (146) и (147) представляют собой алгоритм управления в системе привода робота i-й степени подвижности, реализуемый в микропроцессоре. На заключительном участке переходного процесса i-я система привода работает как следящая система с экспоненциальной переходной функцией, соответствующей плавному позиционированию звена с малыми по амплитуде упругими колебаниями.
Для привода переменного тока синтезируемым сигналом управления является частота напряжения на обмотке двигателя. Для асинхронного двигателя пользуемся формулами (53), (56), (61), (65).
Рассмотрим построение следящей системы. Здесь главным является наилучшее приближение регулируемой величины н заданию. Интегральный критерий задают в виде 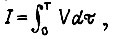 где
где 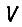 - квадратичная форма от фазовых координат и управлений,
- квадратичная форма от фазовых координат и управлений, 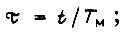

Минимизируя интегральный критерий
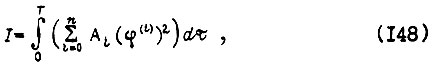
где 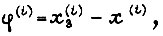
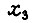 - задание;
- задание; 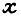 - действительное значение координаты;
- действительное значение координаты; 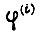 - ошибка, получаем плавный, без резких колебаний, и достаточно быстрый переходный процесс Характер его определяется выбранными значениями весовых коэффициентов
- ошибка, получаем плавный, без резких колебаний, и достаточно быстрый переходный процесс Характер его определяется выбранными значениями весовых коэффициентов 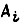 Уравнение экстремали получаем, решив уравнение Эйлера - Пуассона:
Уравнение экстремали получаем, решив уравнение Эйлера - Пуассона:
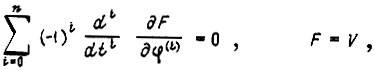
где n - порядок дифференциального уравнения объекта управления. Задачу можно решать поэтапно. Сначала из уравнения экстремали с учетом граничных условий находим оптимальное значение n-й производной регулируемой величины. Затем определяем оптимальное управление, исходя из заданного уравнения объекта.
Отыщем оптимальное соотношение между координатами системы 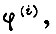 решив уравнение Эйлера - Пуассона для критерия оптимальности, заданного в квадратичной форме.
решив уравнение Эйлера - Пуассона для критерия оптимальности, заданного в квадратичной форме.
Это соотношение имеет вид
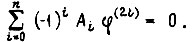
Когда верхний предел интегрирования в выражении для критерия оптимальности 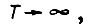 а значение координат
а значение координат 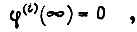 то дифференциальное уравнение экстремали есть
то дифференциальное уравнение экстремали есть 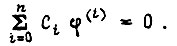
Коэффициенты 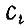 находят через коэффициенты
находят через коэффициенты 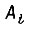 по формуле
по формуле
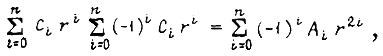
где r - корень характеристических уравнений, соответствующих дифференциальным уравнениям с коэффициентами 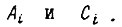 Зная оптимальное соотношение между координатами системы, можно найти оптимальное значение n-й производной регулируемой величины по формуле
Зная оптимальное соотношение между координатами системы, можно найти оптимальное значение n-й производной регулируемой величины по формуле
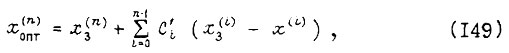
где 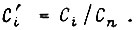
Для объекта, описываемого линейным дифференциальным уравнением первого порядка 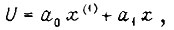 и критерия оптимальности
и критерия оптимальности
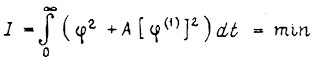
оптимальное соотношение между координатами системы имеет вид 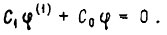 Оптимальное значение первой производной регулируемой величины
Оптимальное значение первой производной регулируемой величины 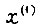 есть
есть 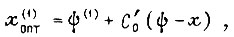
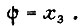 Подставив
Подставив 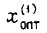 в уравнение объекта управления, получаем
в уравнение объекта управления, получаем
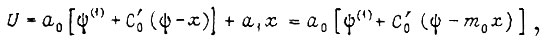
где 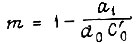 - коэффициент обратной связи по регулируемой величине. Коэффициенты Ci и C0' находим из равенства
- коэффициент обратной связи по регулируемой величине. Коэффициенты Ci и C0' находим из равенства 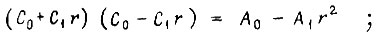 так как
так как 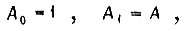 то
то 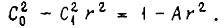
Для устойчивого эйлеровского регулятора данное равенство выполняется, если 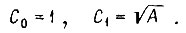 Тогда уравнение экстремали имеет вид
Тогда уравнение экстремали имеет вид
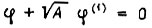
или
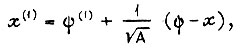
т. е. 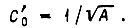
Структурная схема следящей системы, соответствующая выведенному закону управления 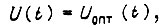 представлена на рис. 41. В этой схеме отсутствует возмущение объекта управления, что нашло отражение и в законе
представлена на рис. 41. В этой схеме отсутствует возмущение объекта управления, что нашло отражение и в законе 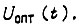
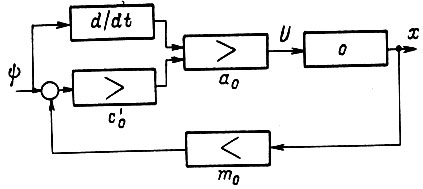
Рис. 41
Если задан объект управления, описываемый линейным дифференциальным уравнением n-го порядка
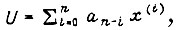
и требуется найти оптимальное управление, при котором минимизируется критерий качества
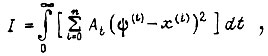
то управление 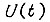 определяем по формуле
определяем по формуле
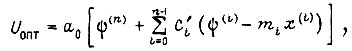
где 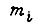 - коэффициент обратной связи по i-й координате:
- коэффициент обратной связи по i-й координате:
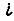
Коэффициенты 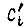 определяются аналогично предыдущему случаю.
определяются аналогично предыдущему случаю.
Таким образом, для оптимального управления объектом n-го порядка требуется измерить задание, n его производных, регулируемую величину и ее 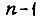 производных.
производных.
Пусть на линейный объект n-го порядка действует некоторое возмущение λ. Примем, что возмущение действует на вход некоторой части объекта совместно с промежуточной величиной 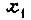 . Связь между
. Связь между 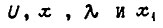 описывается следующими дифференциальными уравнениями:
описывается следующими дифференциальными уравнениями:
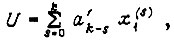
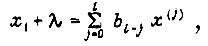
где k - порядок объекта до места входа возмущения, причем 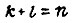 Исключив промежуточную величину
Исключив промежуточную величину 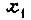 , получим
, получим
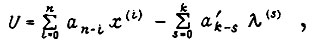
где 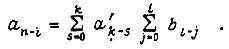 Оптимальное управление
Оптимальное управление
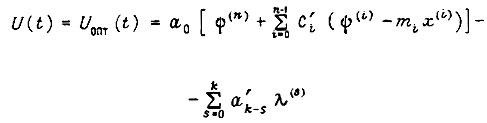
или
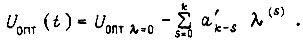
Здесь 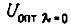 - оптимальное управление при отсутствии возмущения.
- оптимальное управление при отсутствии возмущения.
Для электродвигателя постоянного тока независимого возбуждения, не учитывая индуктивности якорной обмотки 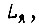 силы трения и наличия контура компенсации волновых колебаний звена робота, получим следующие уравнения:
силы трения и наличия контура компенсации волновых колебаний звена робота, получим следующие уравнения:
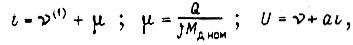
т. е.
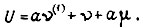
Если 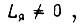 то
то 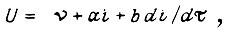 где
где 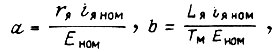
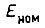 - номинальная э.д.с,
- номинальная э.д.с, 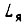 - индуктивность.
- индуктивность.
Тогда уравнение объекта управления получает вид
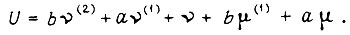
Считая, что 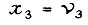 - заданная скорость вращения вала,
- заданная скорость вращения вала, 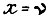 - действительная скорость, получаем оптимальное значение первой производной от
- действительная скорость, получаем оптимальное значение первой производной от 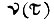 при
при 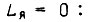
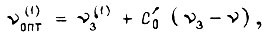
где 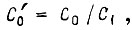 и оптимальное значение второй производной от
и оптимальное значение второй производной от 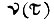 при
при 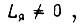 :
:
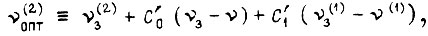
где  Коэффициенты, являющиеся постоянными интегрирования дифференциального уравнения экстремали, зависят от граничных условий
Коэффициенты, являющиеся постоянными интегрирования дифференциального уравнения экстремали, зависят от граничных условий 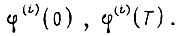 Если, например,
Если, например, 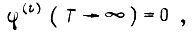 то это исключает решения дифференциального уравнения экстремали, приводящие к неустойчивости регулятора, и приводит к учету определенной полярности значений
то это исключает решения дифференциального уравнения экстремали, приводящие к неустойчивости регулятора, и приводит к учету определенной полярности значений 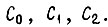 Формулы оптимального управления
Формулы оптимального управления 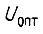 получаем подстановкой в уравнение объекта
получаем подстановкой в уравнение объекта 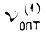 при
при 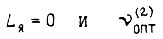 при
при 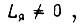 :
:
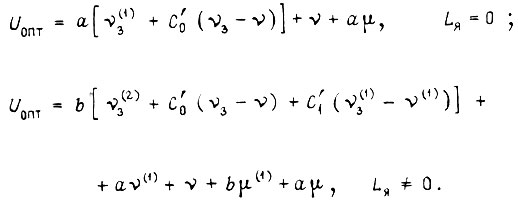
Перепишем эти формулы:
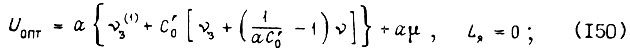
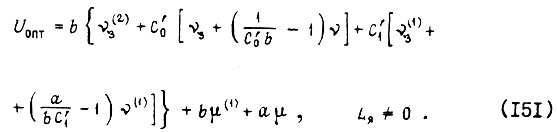
При 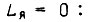 коэффициенты Ci определяем из уравнения
коэффициенты Ci определяем из уравнения 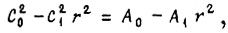 откуда
откуда 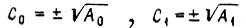 Устойчивому регулятору соответствуют коэффициенты
Устойчивому регулятору соответствуют коэффициенты 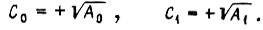 Уравнение экстремали
Уравнение экстремали 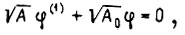 коэффициент
коэффициент 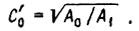 При
При 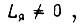 коэффициенты Ci определяем из уравнения
коэффициенты Ci определяем из уравнения 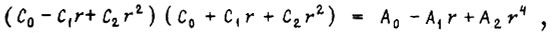 откуда
откуда 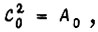
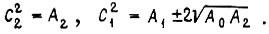
Аналогично находим оптимальное управление в следящей системе, когда выходной координатой объекта управления является путь, проходимый электродвигателем, и его уравнения имеют вид
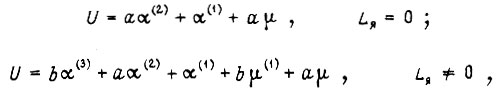
а критерием оптимальности являются интегралы
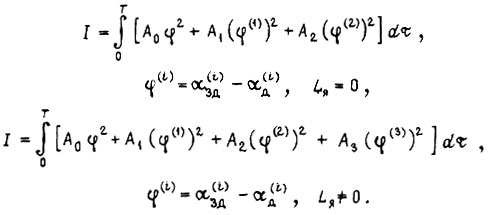
Применяя "принцип максимума" вместо рассмотренного классического метода для позиционного привода и для следящей системы можно получить управления релейного типа. При этом автоматически решается вопрос удовлетворения условию ограничения управления. Такие системы можно использовать, если незначительны вибрации скорости и момента привода, вносимые управлением.
Синтезируем по аналогии с рассмотренным выше управление в следящей системе с асинхронным электродвигателем. За регулируемый параметр двигателя принимаем напряжение на обмотке статора. Уравнение механической характеристики двигателя запишем следующим образом:
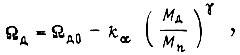
где 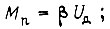
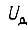 - напряжение обмотки статора;
- напряжение обмотки статора; 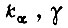 и
и 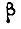 - постоянные коэффициенты.
- постоянные коэффициенты.
Из вида механической характеристики следует формула 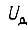 :
:
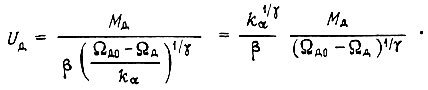
Момент, развиваемый двигателем, есть сумма
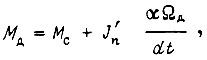
где 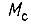 - вращающий момент в шарнире робота с учетом силы трения;
- вращающий момент в шарнире робота с учетом силы трения; 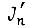 - момент инерции вала двигателя и редуктора, приведенный к двигателю.
- момент инерции вала двигателя и редуктора, приведенный к двигателю.
Тогда 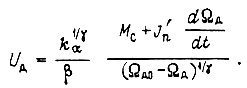 Угол поворота для вала двигателя
Угол поворота для вала двигателя 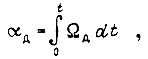 поэтому
поэтому
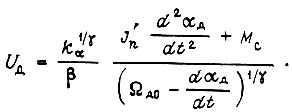
Примем, что электронный преобразователь, включенный перед двигателем, является безынерционным с коэффициентом усиления 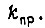 Напряжение на его выходе
Напряжение на его выходе 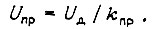
Минимизируем функционал
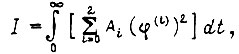
где 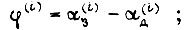
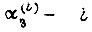 -я производная по времени от задания по углу поворота вала двигателя.
-я производная по времени от задания по углу поворота вала двигателя.
Уравнение экстремали 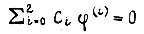 или
или 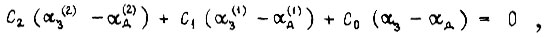 отсюда получаем
отсюда получаем
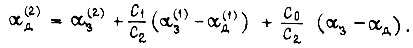
Величины 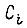 определяем из уравнения
определяем из уравнения 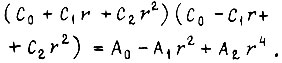 Напряжение на входе электронного преобразователя
Напряжение на входе электронного преобразователя
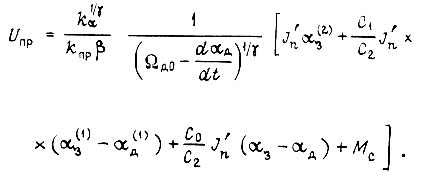
Если задание по углу есть 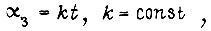 то
то
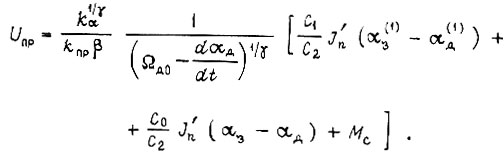
На рис. 42 показана структура следящей системы, реализующая управление 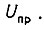
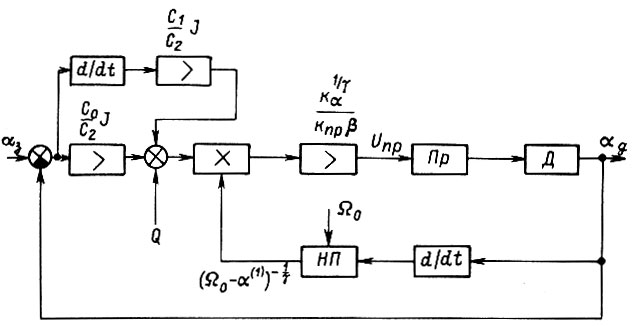
Рис. 42
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'