7. Обратимая система привода

Представим, что обратимая система привода, содержащая механически несвязанные задающий и исполнительный механизм, описывается уравнениями в операторной форме:

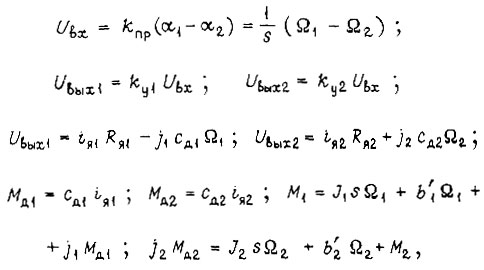
где 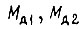- моменты сил на валах двигателей; 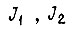- приведенные к выходным валам суммарные моменты инерции; 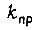- коэффициент преобразования разности углов поворота 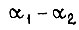на выходных валах в напряжение входа усилителей 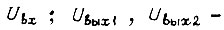- напряжения выходов усилителей; 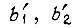- коэффициенты вязкого трения кинематических цепей механизмов; 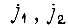- передаточные числа редукторов; 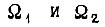- угловые скорости вращения вала задающего механизма и вала исполнительного механизма; 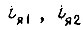- токи двигателей; 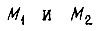- моменты сил на выходных валах. Решение системы уравнений имеет вид

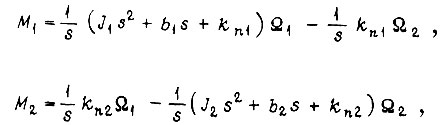
где

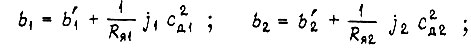
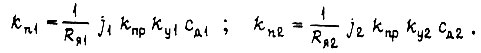
Теперь представим, что оператор воздействует на нагрузку через промежуточное устройство, которым является механический вал с двумя сосредоточенными массами на концах. Имеем систему уравнений

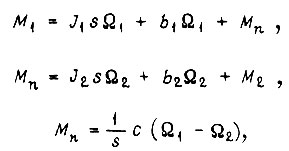
где 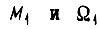- момент и скорость вала со стороны оператора; 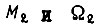- момент и скорость на выходе вала; 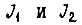- моменты инерции масс; 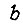- коэффициент скоростного трения; 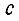- коэффициент жесткости; 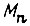- момент на упругом элементе. Решение системы относительно :

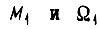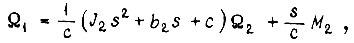
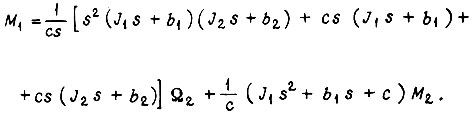
Для стационарного режима, когда 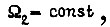через промежуточное устройство без искажений передается информация о скорости 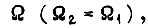а передача момента происходит с искажениями .зависящими от коэффициентов 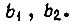В переходном режиме искажения 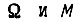тем больше, чем больше моменты инерции перемещающихся масс 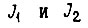и коэффициенты скоростного трения 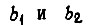Углы поворота на концах вала: 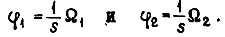Очевидно,

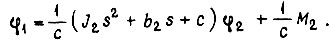
В установившемся режиме имеет место статическая ошибка 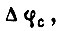величина которой прямо пропорциональна моменту нагрузки 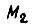обратно пропорциональна коэффициенту жесткости механической передачи .

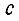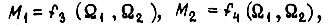Если от полученных формул для упругого механического вала перейти к функциям то увидим, что моменты на входе и выходе 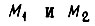имеют такую же функциональную зависимость как и моменты на входе и выходе обратимой системы привода. При условии идентичности двигателей и кинематических цепей, т. е. при выполнении равенств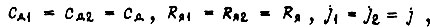 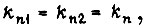работа обратимой системы привода аналогична работе упругого механического вала. Коэффициент передачи разомкнутой цепи привода тождествен коэффициенту жесткости упругого механического вала.

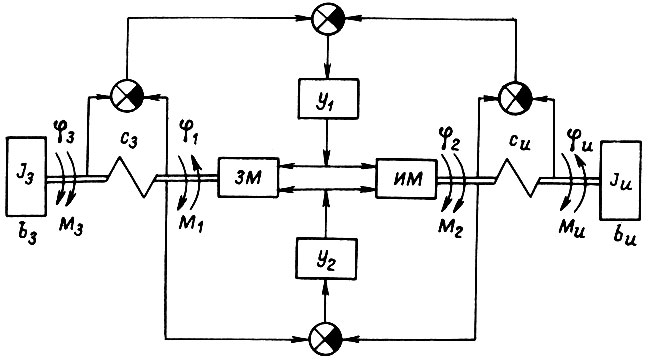
Рис. 51

Работа копирующего манипулятора складывается из выполнения разнообразных операций по обслуживанию технологического процесса (монтаж и демонтаж оборудования, перенос и укладка предметов, выполнение лабораторных работ). Этому соответствуют четыре режима работы схемы, показанной на рис.51.

1. Режим вынужденного движения 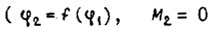или
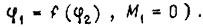
2. Режим короткого замыкания 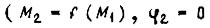или
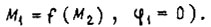
3. Режим свободного движения
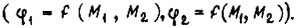
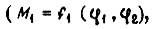
4. Режим наложенного вынужденного движения 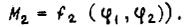Здесь при отсутствии скручивающихся валов 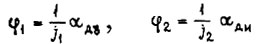(первый и второй каналы i-го привода),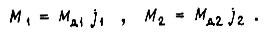

Исходя из матричной формы записи

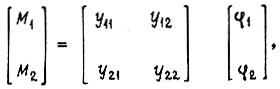
получим в режиме вынужденного движения уравнения

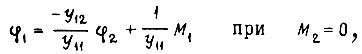
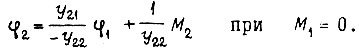
Эти уравнения приводятся к виду

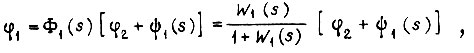
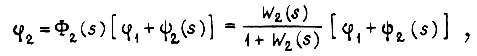
где 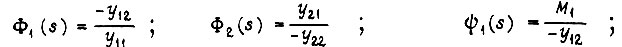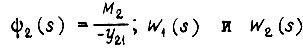- передаточные функции разомкнутых задающего и исполнительного каналов.

В режиме короткого замыкания, исходя из матричной формы записи

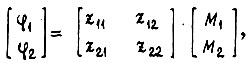
получим уравнения

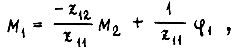
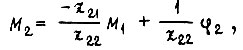
которые приводятся к виду

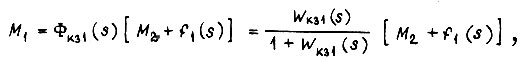
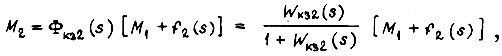
где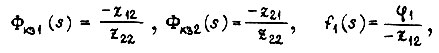

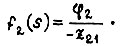
Здесь

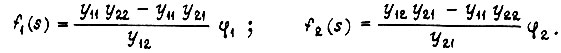
В режиме свободного движения

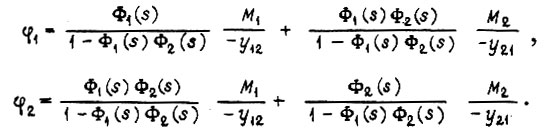
Отсюда

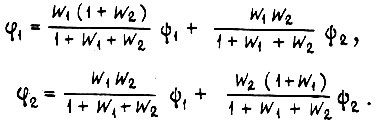
Если 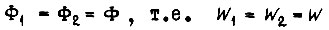, то

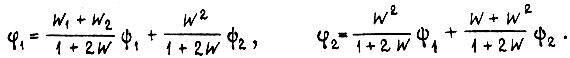
Устойчивость движения симметричной системы обратимого привода определяется с помощью характеристического уравнения 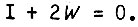Трактовка критерия устойчивости, по Найквисту, ведется не относительно точки с координатами 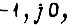относительно точки с координатами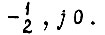

Режим наложенного вынужденного движения позволяет выяснить, какие силовые реакции возникают на входе и выходе системы при одновременном изменении координат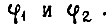

При анализе системы обратимого привода необходимо учитывать наличие внешних кинематических цепей. Например, для схемы на рис. 51, где двигатели с силовыми преобразователями включены в ЗМ и ИМ, имеем

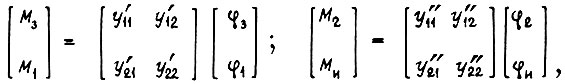
где 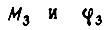- момент и угол на входе ЗМ; 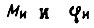- момент и угол на выходе ИМ; 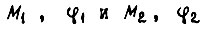- моменты и углы на входе и выходе собственного контура системы обратимого привода. Формулы 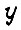- параметров имеют вид

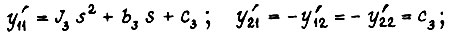
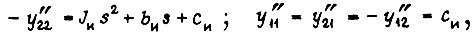
где 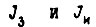- эквивалентные моменты инерции движущихся элементов кинематических цепей ЗМ и ИМ; 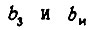- коэффициенты скоростных потерь в цепях ЗМ и ИМ; 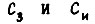- коэффициенты жесткости валов, показанных на рис. 51.

Синтез динамических свойств системы обратимого следящего привода проводится для каждого из возможных режимов работы манипуляторов с использованием известной теории синтеза систем привода в частотной области. В работе [4] рассматривается, кроме того, вопрос построения инвариантной системы обратимого привода. Обычно под инвариантностью понимается независимость какой-либо регулируемой координаты от возмущающего воздействия. В обратимом же приводе внешние координаты (углы и моменты) не могут быть однозначно разделены на регулируемые и возмущающие. Обеспечить инвариантность здесь означает выявить и реализовать условия независимого управления разномерными компонентами мощности (скоростью, моментом) при сохранении функциональной связи между мощностями на входе и выходе обратимого привода.