2. Электрогидравлические следящие системы с дроссельным управлением

Электрогидравлические следящие системы можно разделить на две группы:

1. системы, применение которых вызвано не требованием высокого быстродействия, а другими соображениями;
2. следящие системы, к которым предъявляются жесткие требования по быстродействию. В этом случае необходимо учитывать сжимаемость жидкости.

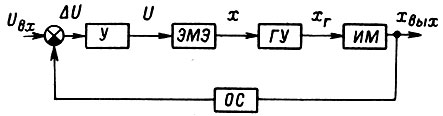
Рис. 56

На рис. 56 изображена схема следящей системы, где обозначены: У - усилитель ошибки, ЭМЭ - электромеханический элемент, ГУ - гидроусилитель, ИМ - гидравлический исполнительный механизм, ОС - элемент обратной связи. Работа элементов схемы для следящей системы первой группы описывается уравнениями

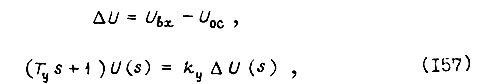
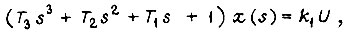
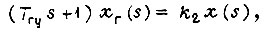
где 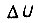- электрическое напряжение, характеризующее сигнал ошибки; 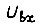- сигнал входа; 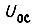- сигнал обратной связи; 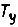- постоянная времени усилителя 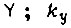- его коэффициент передачи; 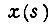- сигнал входа 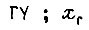- перемещение на выходе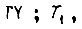 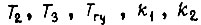- коэффициенты, принимаемые постоянными; 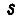- параметр преобразования Лапласа - Карсона; начальные условия - нулевые.

Гидравлический исполнительный механизм представим в виде последовательно соединенных трех звеньев: интегрирующего, усилительного и запаздывающего. Время запаздывания определяется наличием неучтенных малых параметров системы. В наиболее простом виде уравнение движения исполнительного механизма в операторной форме получает вид [28]

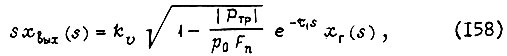
где 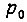- давление в напорной магистрали; 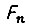- эффективная площадь поршня; 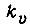- крутизна скоростной характеристики холостого хода гидравлического исполнительного механизма с идеальным золотником; 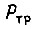- сила или момент силы трения, действующие на поршень или выходной вал гидромотора.

Последнее уравнение записано для случая,когда перепад давления на поршне гидроцилиндра 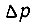уравновешен только силой или моментом силы трения. В общем случае перепад давления уравновешен суммой внешних сил, действующих на выходной шток гидроцилиндра;

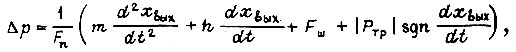
где 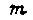- масса, линейно перемещаемая поршнем гидроцилиндра (без учета масс звеньев рабочего органа робота); 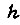- коэффициент вязкого трения нагрузки, приведенный к поршню; 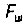- сила сопротивления со стороны рабочего органа.

Для вращательного движения, создаваемого гидромотором:

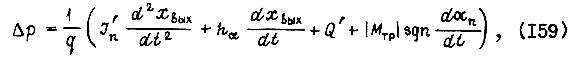
где 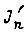- момент инерции вала привода, приведенный к гидромотору; 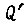- приведенный к гидромотору вращающий момент в шарнире рабочего органа робота; коэффициент 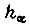характеризует вязкое трение; 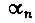- угол поворота выходного вала привода; 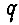- удельный объем гидромотора (объем гидромотора, приходящийся на I рад угла поворота его выходного вала).

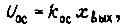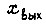При наличии только жесткой отрицательной обратной связи по перемещению поршня силового гидроцилиндра имеем где - перемещение на выходе системы (см. рис. 56).

Если для коррекции следящей системы используются также сигналы, пропорциональные скорости и ускорению выходного штока, то напряжение сигнала обратной связи записывается в виде

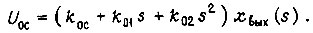
Уравнение движения следящей системы с учетом такой формы 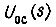и (157), (158) имеет следующую запись:

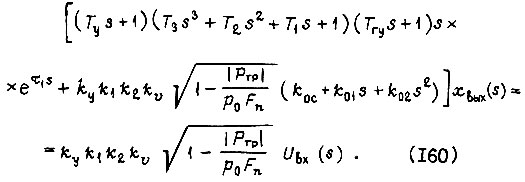
Если управление в системе электрогидропривода рассматриваемой степени подвижности робота ведется на каждом достаточно малом отрезке времени 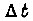с ускорением выходного вала привода 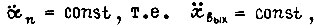и при этом приращения скорости и пути практически незначительны, то величина 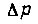в формуле (159) может быть принята постоянной на 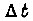. Тогда можем воспользоваться приближенным уравнением переходного процесса в следяющей системе внутри данного 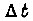, заменив для вращательного движения в формуле (160) величину 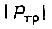на

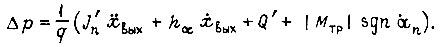
Для следящих систем второй группы уравнение поступательного движения гидравлического исполнительного механизма с учетом снижаемости жидкости можно записать на основе уравнения скоростной характеристики [28]

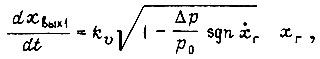
где 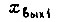- перемещение сечений жидкости, находящихся вблизи торцевых стенок гидравлического исполнительного механизма, и уравнения упругих деформаций

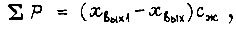
где 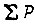- сумма сил, действующих на поршень; 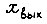- перемещение поршня гидроцилиндра; 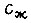- жесткость жидкости, приведенная к поршню.

Объединение двух уравнений дает

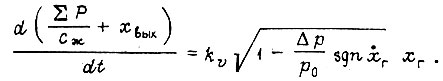
Используя соотношение 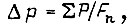получаем

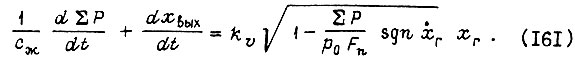
Уравнение (161) является общей формой дифференциального уравнения движения нагруженного гидравлического исполнительного механизма дроссельного управления с учетом сжимаемости жидкости. Для вращательного движения это уравнение в развернутой форме

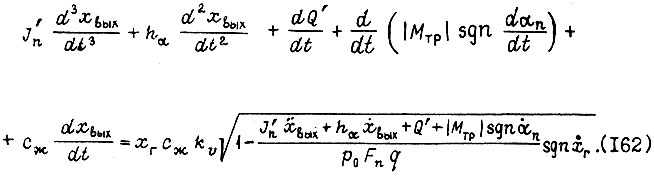
Допустив на малом отрезке времени 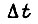постоянство суммарного момента сил сопротивления, приведенного к гидромотору, перейдем от (162) к линейному дифференциальному уравнению. Решая полученное таким образом уравнение движения гидромотора совместно с системой (157), придем к формуле переходного процесса на отрезке 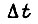в электрогидравлической следящей системе, замкнутой по схеме, показанной на рис. 56.

Коэффициенты 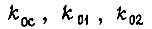находят из желаемой формы кривой переходного процесса замкнутой системы. Для известных коэффициентов 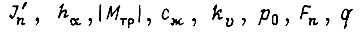уравнения (162) и 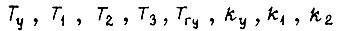системы уравнений (157) можем получить общую формулу действительной части амплитудно-фазовой частотной характеристики электрогидравлической системы для неизвестных по величине При этом электрогидравлический привод представляется как линейный преобразователь с постоянным моментом сил сопротивления, т. е. такое представление справедливо на малом отрезке времени, когда скорость вращения вала привода и путь существенно внутри 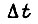не изменились. Момент сил сопротивления заменяется константой в формуле (162). В соответствии с (93) получаем общую формулу переходного процесса 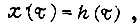после чего, зная желаемую форму кривой 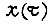подбираем коэффициенты 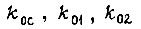для различных значений суммарного момента сил сопротивления на валу привода. Располагая 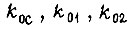как функциями момента, вводим их в специально изготовленные устройства, корректирующие во время эксплуатации следящей системы коэффициенты передачи обратных связей, но сохраняя их постоянными внутри каждого отрезка времени 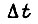. Того же результата достигаем, реализовав алгоритм подстройки коэффициентов 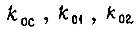в функции момента сопротивления в микропроцессоре, подключенном к системе привода.

Проблема измерения моментов сил, действующих в шарнирах рабочих органов роботов и на валах двигателей, является всегда сложной. От ее решения часто зависит целесообразность использования того или иного варианта привода. Один из косвенных способов измерения, изложенный выше при рассмотрении вопросов динамики систем электропривода, заключается в вычислении момента по измеренным внутри 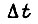фазовым координатам. Управление в системе привода на следующем отрезке 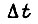вычисляется в предположении, что момент сопротивления сохраняет ту же величину, которую он имел на предыдущем отрезке. Такой подход применим и к электрогидравлической следящей системе. Он дает тем меньшую ошибку, чем меньше необходимая величина 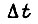, требующаяся для измерения фазовых координат. Кроме того, в желаемой кривой переходного процесса должны отсутствовать скачки ускорения на выходном валу привода. Тогда при идеальной реализации желаемых динамических свойств системы привода каждой степени подвижности робота отсутствуют скачки и в величинах вращающих моментов в шарнирах рабочего органа (см., например, формулы (3), (4), (5)) при переходе от одного отрезка 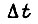к другому. При этом управление, реализованное исходя из предположения о неизменности суммарного момента сопротивления на выходном валу привода внутри соседних отрезков времени, приводит к результатам, близким к желаемым.

К синтезу электрогидравлической следящей системы применим также в полной мере вариационный метод (§ 5 гл. 2) для следящего электропривода. Принципиально здесь не требуется линеаризация гидравлического исполнительного элемента, описываемого, например, дифференциальным уравнением (162). Структура оптимального регулятора после решения задачи синтеза оптимального управления во временной области отразит всю нелинейность исполнительного элемента. В дальнейшем может потребоваться аппроксимация функции управления из требования максимальной простоты инженерного решения.

Наконец, идея построения цифровой следящей системы электропривода с контуром регулирования ускорения (§ 6 гл. 2) также применима к гидравлической системе. По аналогии с транзисторной схемой ШИП гидроусилитель, управляющий гидромотором, может работать в режиме широтно-импульсного преобразователя, у которого ширина рабочих импульсов на выходе зависит от электрических сигналов.