2. Построение блока памяти системы привода

Блок БПП - это логическая схема, которая имеет определенное число двоичных выходов, образующих затем двоичную или десятичную форму сигнала 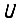. Представим, что каждый выходной сигнал принадлежит своей части схемы, не связанной логически с другими частями БПП. Каждую такую часть назовем узловой схемой (УС) (рис. 60). Информация о 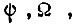поступает в виде конъюнкций состояний разрядов двоичных чисел 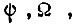от блока конъюнкций БК внутри отрезков 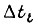параллельно на входы всех УС. 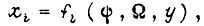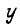Один выходной сигнал есть булева функция где - состояние элементов памяти, входящих в данную узловую схему. Для n двоичных переменных имеем 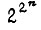булевых функций. Отсюда следует, что число элементов памяти, входящих в одну схему УС, равное 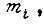определяется из равенства 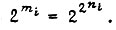Это означает, что число 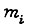должно быть равно числу наборов переменных, связанных через БК со входом УС, т. е. 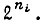Число 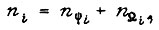и где 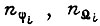- количества двоичных разрядов соответственно 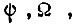поданных на вход БК, для которых образованы всевозможные конъюнкции, поступающие к i-ой узловой схеме. Каждая конъюнкция появляется только на своем выходе БК. Узловая схема реализует формулу

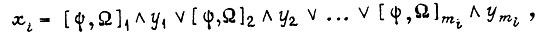
где 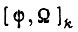- k-я конъюнкция состояний разрядов 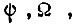; 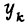- состояние k-го элемента памяти.

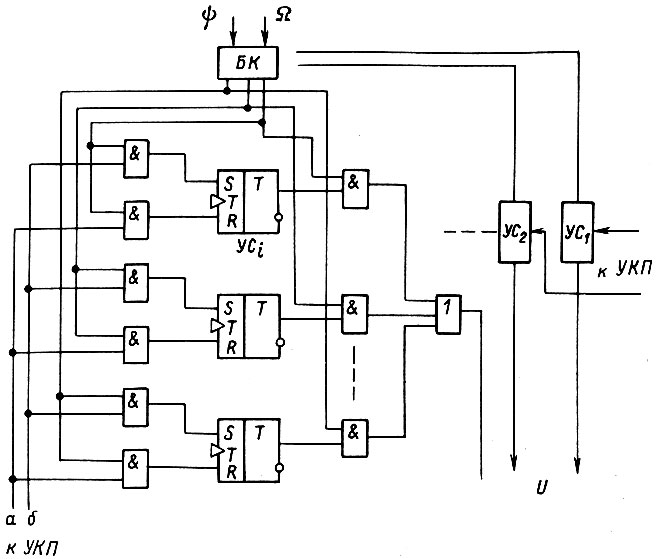
Рис. 60

Эта формула определяет простой способ построения узловых схем и всего БПП в целом (см. рис. 60). Правый ряд элементов "и" пропускает к выходу УС информацию о состоянии элемента памяти, связанного с конъюнкцией состояний разрядов 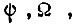имеющей место в рассматриваемый момент времени. С помощью левого ряда элементов си> осуществляется коррекция, т. е. переключение в нулевое или единичное положения триггера данной конъюнкции в зависимости от рассогласования между величиной φ внутри паузы 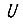и величиной 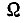внутри импульса. Блок конъюнкций содержит только элементы "И". Общее число элементов <И> блока равно числу - всех конъюнкций состояний разрядов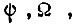

Общее количество элементов БПП определяется максимальным рабочим ускорением 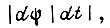погрешностью обучения, передаточными свойствами силовых преобразователей, номинальными данными двигателя, постепенными изменениями параметров системы во времени.

Неустановившееся движение привода описывается уравнением

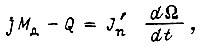
где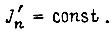

Если максимальные и минимальные ускорения 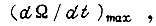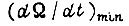соответствуют рабочим пределам 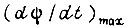и 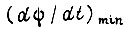и появление любого значения вдоль оси времени на протяжении эксплуатации привода равновероятно, тогда средневероятностное ускорение

Для электродвигателя, считая момент двигателя 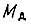пропорциональным току обмотки, т. е. 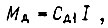при 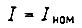получаем номинальный момент 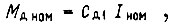который должен быть равен среднеквадратичному моменту. Средняя величина вращающего момента в шарнире

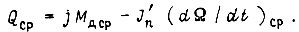
При двойной максимально допустимой перегрузке по току получаем 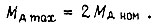Для ускорения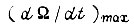

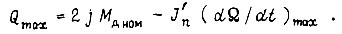
Если все значения 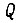между 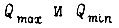равновероятны, тогда

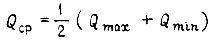
и

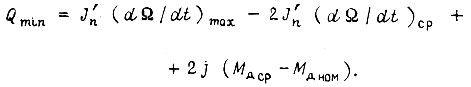
Инерционность привода проявляется более всего в величине ошибки регулирования для сигнала управления 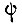, имеющего максимальную производную по времени. Допустим, сигнал 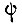с постоянной производной 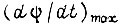приложен к входу системы, начиная с 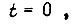и действует во всем диапазоне скоростей 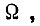ограниченном рабочими пределам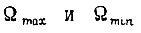и при 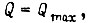причем начальная скорость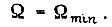

В некоторой точке 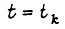сигнал 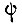достигает величины 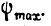Если бы привод не имел инерционности, а сигнал 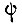был бы непрерывным, в этой же точке привод достиг бы скорости 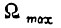без учета действия БПП. Истинная скорость 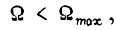ее величина при 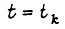может быть найдена, если известна переходная функция силовой части 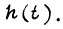Назначение БПП состоит в том, чтобы добавочными управлением силовой части электропривода обеспечить компенсацию ошибки регулирования, вызванной его инерционностью. Если сигналу 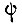придается размерность 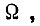, то эта ошибка равна разности 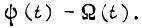Поскольку в общем случае передаточная характеристика силовой части нелинейна при изменении 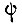, то чтобы не допустить ускорений, больших 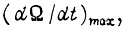выбираем 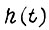такой, которой соответствует наибольший коэффициент усиления СЧ. Выбрав функцию 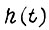, которая описывает теперь линейную систему, при 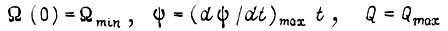вычисляем скорость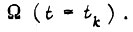

Анализируя при различных 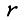сумму

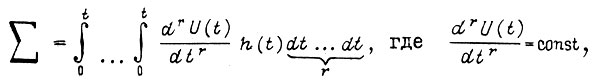
находим такую функцию 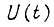с наименьшей максимальной амплитудой, для которо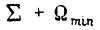й при 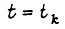равна 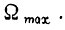Если при этом для всех 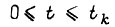сумма 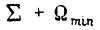расположена не ниже функции 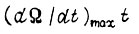и наиболее близко к ней, а ускорение 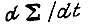допустимо для двигателя и механизма, т. е. расположено рядом с 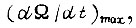то величина 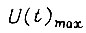есть максимальный требуемый сигнал выхода логической схемы 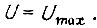Эта операция наиболее легко может быть выполнена, если 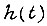описывает экспоненциальный переходный процесс. 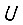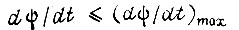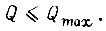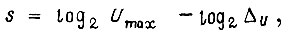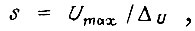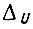Найденная величина гарантирует отсутствие недопустимой перегрузки двигателя, если всегда и Число узловых схем определяем по формулам для двоичного выхода БПП для десятичного же выхода БПП (при обычном сложении выходных сигналов двочных узловых схем), где - наименьшая величина 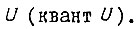Здесь не учтены избыточность элементов БПП и постепенные изменения параметров привода во времени.

Логическая схема упрощается, если желаемое число различных значений сигналов 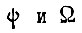не исчерпывает всего диапазона, заключенного между рабочими пределами. Например, если из ста потребных комбинаций значений 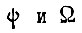за всю эксплуатацию привода на каждом достаточно большом участке времени необходимо наилучшее механическое движение только для всегда известных десяти комбинаций, то можно построить логическую схему, обучающуюся распознаванию 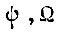по типу персептрона Ф. Розенблатта и имеющую только десять выходов. Эти выходы подаются затем в блок БПП.

Приближение состояния элементов памяти к требуемому в процессе обучения происходит по рекомендации, выдаваемой устройством коррекции памяти. Заметим, что эта рекомендация может быть получена путем количественно'; оценки ошибки регулирования и учета ее в величине коррекции или при отсутствии этой оценки. Первый способ назовем обучением по алгоритму, второй - обучением путем перебора всех состояний. Очевидно, второй способ приемлем, когда необходимо обучение электропривода, но не предусмотрена адаптация, ибо в этом случае при переобучении (адаптации) во время эксплуатации нормальная работа робота невозможна. Схема устройства коррекции памяти вырождается здесь практически в генератор одиночного импульса для каждой коррекции, подаваемого в двоичный счетчик, собранный из всех элементов памяти БПП. Длительность обучения возрастает и может оказаться в некоторых случаях неприемлемой.

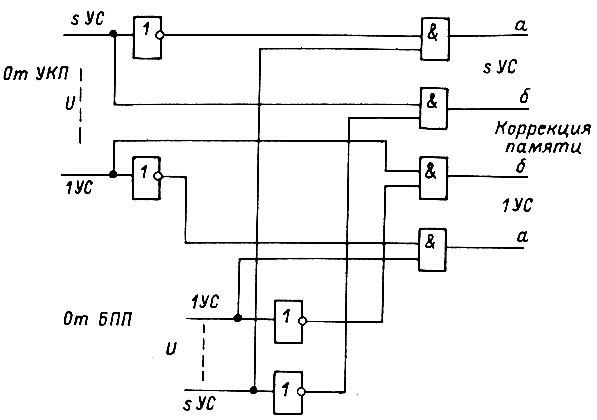
Рис. 61

На рис. 61 изображена выходная часть схемы УКП для системы привода, обучающейся по алгоритму. Выходы 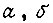те же, что и входы 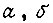в схеме на рис. 60.

В работе [26] рассмотрены комбинированные обучающиеся системы управления сложными процессами, названные детерминированными самообучающимися системами. В них отсутствует поиск, т. е. требуемое управление реализуется мгновенно, но появляется проблема идентификации объекта управления. В применении к приводу в понятие объекта здесь следует включить механизм, двигатель и силовые преобразователи. Реализация этого принципа обучения затруднена, если задана высокая точность организации движения, что связано с необходимостью иметь очень большое количество логических элементов и с завышением стоимости обучающейся системы.

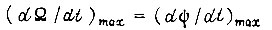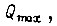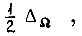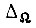Максимальное ускорение развиваемое приводом при и заданная точность обучения по скорости где - наименьшая абсолютная величина ступеньки, с помощью которой формируется кривая 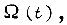определяют минимальную длительность импульса сигнала 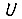на выходе логической схемы БПП:

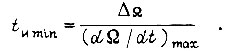
Высота ступеньки 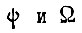зависит от заданной точности формирования 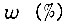скорости вращения 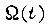для произвольного момента времени

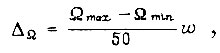
откуда максимальное число ступенек равно 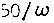Высота наименьшей ступеньки выходного сигнала БПП 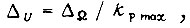где 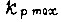- коэффициент усиления звеньев силовой части. За промежуток времени 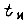система привода успевает догнать задающий сигнал 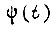до величины 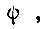заданной в начале импульса. Найденное выше значение 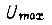гарантирует ускорение 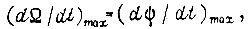если переходная функция 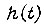взята для наибольшего усиления СЧ. Обозначим через 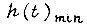переходную функцию, для которой 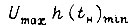за промежуток 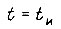минимально. Длительность импульса и найдем из выражения 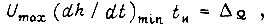где 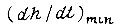- производная от функции 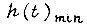по времени, представленная постоянной в пределах 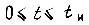Отсюда

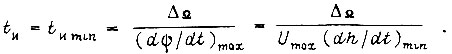
Такая длительность импульса 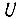обеспечивает ликвидацию рассогласования между величиной 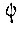в начале и в конце импульса, равного 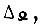для любой формы сигнала 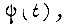заключенного между 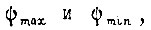если ускорение 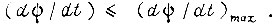При проектировании логической схемы следует учитывать такие постепенные изменения параметров привода, т. е. изменения во времени функции 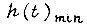вводя на нежелательные изменения поправку в величину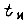

Рассогласование 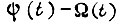в полностью обученной системе привода нарастает на каждом отрезке дискретизации времени как в пределах импульса 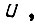так и в пределах паузы. Поэтому в начале каждого отрезка, если система привода обучена,имеем рассогласование 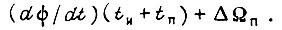Здесь 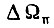изменение скорости вращения привода вследствие управления или при отсутствии его в пределах паузы 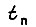сигнала 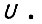Длительность паузы находим из соотношения 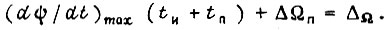При невозможности удовлетворить этому соотношению при 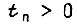берем 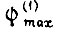меньше принятого ранее.