
3. Анализ процесса обучения системы привода
Рассмотрим случай многократного поступления на вход привода сигнала управления 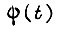 изменяющегося в пределах некоторого цикла. Движение системы привода в последующем цикле обучения определяется результатами ее обучения в предыдущем цикле. Предполагая линейными передаточные свойства привода, т. е. независимость переходной функции
изменяющегося в пределах некоторого цикла. Движение системы привода в последующем цикле обучения определяется результатами ее обучения в предыдущем цикле. Предполагая линейными передаточные свойства привода, т. е. независимость переходной функции 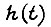 от амплитуды сигнала
от амплитуды сигнала 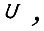 имеем
имеем 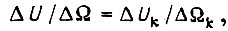 где
где 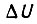 - ступенчатое приращение сигнала на входе СЧ, действующее в промежутке
- ступенчатое приращение сигнала на входе СЧ, действующее в промежутке 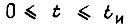 внутри такта обучения длительностью
внутри такта обучения длительностью 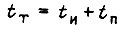 для данной совокупности сигналов
для данной совокупности сигналов 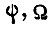 в предыдущем;
в предыдущем; 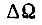 - среднее приращение скорости вращения двигателя в промежутке
- среднее приращение скорости вращения двигателя в промежутке 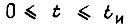 , вызванное появлением
, вызванное появлением 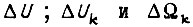 - аналогичные величины, имеющие место после коррекции памяти ЛС и действующие в следующем цикле. Тогда
- аналогичные величины, имеющие место после коррекции памяти ЛС и действующие в следующем цикле. Тогда
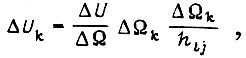
где 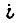 - номер такта;
- номер такта; 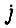 - номер цикла.
- номер цикла.
Обозначим через 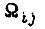 среднюю скорость вращения, которую развивает привод внутри импульса
среднюю скорость вращения, которую развивает привод внутри импульса 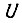 в
в 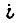 -м-такте и
-м-такте и 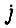 -м цикле обучения. Один из возможных алгоритмов обучения системы привода с нелинейными характеристиками выражается формулой, которую запишем для скорости в первом такте второго цикла:
-м цикле обучения. Один из возможных алгоритмов обучения системы привода с нелинейными характеристиками выражается формулой, которую запишем для скорости в первом такте второго цикла:
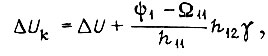
откуда
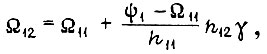
где 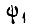 - средняя величина задающего сигнала за
- средняя величина задающего сигнала за 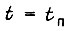 внутри первого такта,
внутри первого такта, 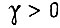 - коэффициент, определяющий алгоритм обучения; предположим, что
- коэффициент, определяющий алгоритм обучения; предположим, что 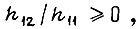 а также для любого
а также для любого 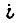 -го такта и
-го такта и 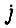 -го цикла
-го цикла 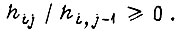
Для третьего и четвертого циклов
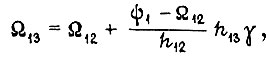
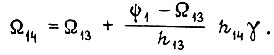
Для 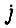 -го цикла
-го цикла
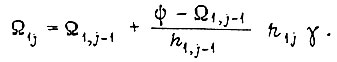
При совместном учете этих формул
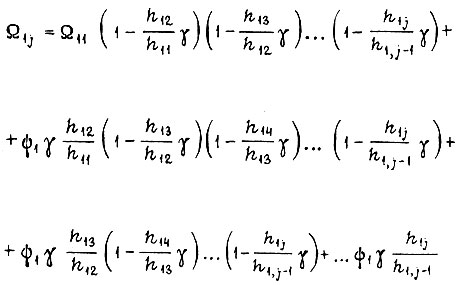
или
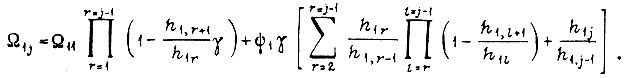
Переходя к линейной системе привода, т. е. полагая 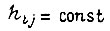 для любого такта и цикла, получаем
для любого такта и цикла, получаем
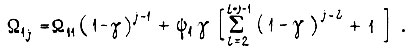
При 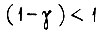 устремим число циклов обучения
устремим число циклов обучения 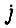 к бесконечности
к бесконечности
Итак, если задана точность обучения 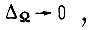 то длительность обучения стремится к бесконечно большой величине. Введем обозначение
то длительность обучения стремится к бесконечно большой величине. Введем обозначение 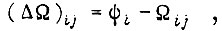 где
где 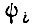 - величина задающего сигнала в начале
- величина задающего сигнала в начале 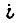 -го такта. Тогда
-го такта. Тогда 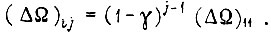 Отсюда находим максимальное число циклов обучения при условии, что рассогласование уменьшилось по абсолютной величине до
Отсюда находим максимальное число циклов обучения при условии, что рассогласование уменьшилось по абсолютной величине до 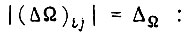
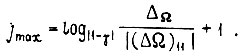
После окончания обучения для заданной кривой 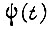 в пределах цикла
в пределах цикла 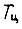 в первом такте
в первом такте 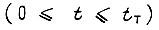 эта же формула определяет максимальное число циклов обучения во втором такте, после полного обучения во втором такте определяет в третьем такте и т. д. В нелинейной системе привода после того, как закончилось обучение в
эта же формула определяет максимальное число циклов обучения во втором такте, после полного обучения во втором такте определяет в третьем такте и т. д. В нелинейной системе привода после того, как закончилось обучение в  -м такте, скорость вращения в
-м такте, скорость вращения в 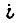 -й такте в
-й такте в 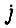 -м цикле
-м цикле 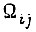 равна
равна
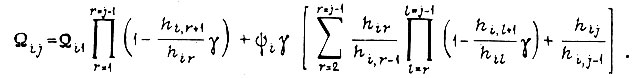
Определим время, затрачиваемое на обучение. Для одной функции 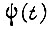 длительность обучения в
длительность обучения в 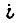 -м такте
-м такте
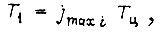
длительность обучения сигналу 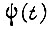 в цикле
в цикле
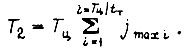
Время организации всей памяти логической схемы
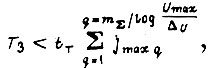
если БПП имеет двоичный выход, и
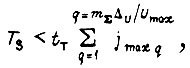
если БПП имеет десятичный выход. Здесь 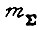 - общее число элементов памяти БПП. Понятие максимального числа циклов обучения связано с минимальным предельным рассогласованием
- общее число элементов памяти БПП. Понятие максимального числа циклов обучения связано с минимальным предельным рассогласованием 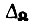 и максимальной величиной начального рассогласования
и максимальной величиной начального рассогласования 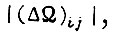 которое всегда меньше абсолютной величины
которое всегда меньше абсолютной величины
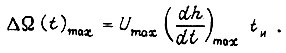
Для нелинейной системы звеньев СЧ
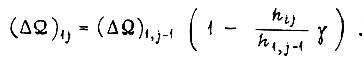
Если коэффициент 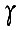 выбран с учетом нелинейности характеристик силовых преобразователей так, что всегда
выбран с учетом нелинейности характеристик силовых преобразователей так, что всегда
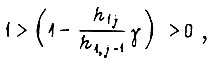
то имеет место процесс приближения скорости вращения 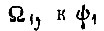 без изменения знака рассогласования
без изменения знака рассогласования 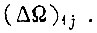 Это справедливо и для остальных тактов. Знак изменяется, если
Это справедливо и для остальных тактов. Знак изменяется, если

При выполнении условия 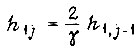 для всех циклов обучение системы представляет собой незатухающие колебания. Если
для всех циклов обучение системы представляет собой незатухающие колебания. Если 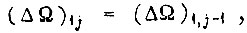 т. е.
т. е. 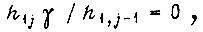 то это соответствует попаданию системы в зону идеального насыщения. Процесс обучения расходится, если
то это соответствует попаданию системы в зону идеального насыщения. Процесс обучения расходится, если 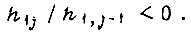
Другой алгоритм обучения - алгоритм коррекции памяти БПП, которая осуществляется тем в большей степени, чем больше рассогласование 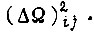 Для заданной функции
Для заданной функции 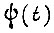 он описывается формулой (в применении к первому такту)
он описывается формулой (в применении к первому такту)
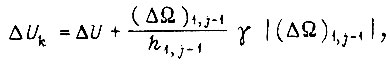
откуда
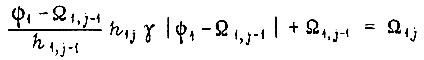
или
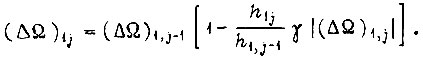
Обучение происходит без изменения знака рассогласования, если
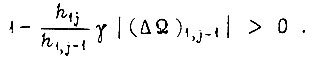
Условие незатухания колебаний
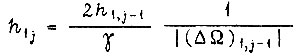
при всех 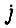 В линейной системе
В линейной системе 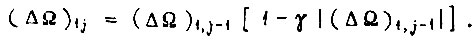 Задав максимально возможное начальное рассогласование
Задав максимально возможное начальное рассогласование 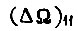 и пользуясь этой формулой, можно определить
и пользуясь этой формулой, можно определить 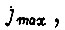 если для последнего цикла движения принять
если для последнего цикла движения принять 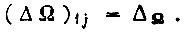
Величина коррекции памяти по первому алгоритму пропорциональна первой степени рассогласования  по второму - квадрату
по второму - квадрату  . Рассмотрим также алгоритм, по которому коррекция производится независимо от величины
. Рассмотрим также алгоритм, по которому коррекция производится независимо от величины  (в применении к первому такту):
(в применении к первому такту):
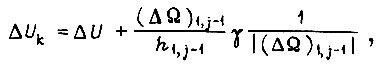
откуда
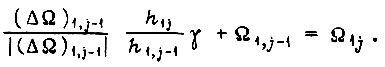
Тогда без изменения знака рассогласования
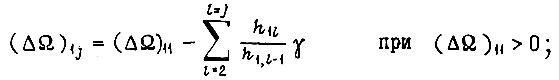
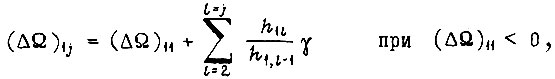
с изменением знака рассогласований
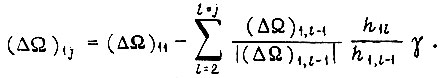
Из формулы
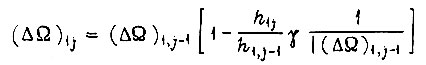
получаем условие неизменности знака рассогласования
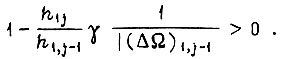
Условие незатухания колебаний скорости в результате обучения
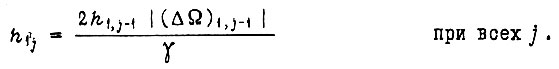
В линейной системе
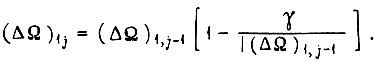
Время, затрачиваемое на обучение системы в одном такте (в данном случае в первом), для заданной функции 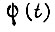 есть
есть
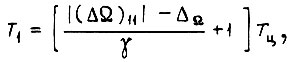
где 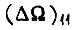 - максимально возможное рассогласование, определяемое величиной
- максимально возможное рассогласование, определяемое величиной 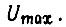 Располагая величиной
Располагая величиной 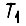 можно рассчитать время, необходимое для обучения системы одной функции
можно рассчитать время, необходимое для обучения системы одной функции 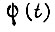 , имеющей цикл
, имеющей цикл 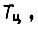 и время полной организации памяти БПП.
и время полной организации памяти БПП.
Каждый из алгоритмов обучения служит основой для проектирования схемы оптимизирующего устройства (УКП) и реализуется ею в процессе вычисления коррекций памяти БПП. Выбор того или иного алгоритма обучения и коэффициентов 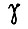 может быть правильно сделан, если имеются сведения о передаточных свойствах силовых преобразователей и двигателей. Общие рекомендации получаем из следующих соображений. В зоне малых ошибок
может быть правильно сделан, если имеются сведения о передаточных свойствах силовых преобразователей и двигателей. Общие рекомендации получаем из следующих соображений. В зоне малых ошибок 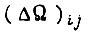 на скорость вращения привода влияют многочисленные неучтенные воздействия. Поэтому детерминированный анализ процессов регулирования в некоторой микрозоне ошибок с точки зрения исследования передаточных свойств привода и формулировки наилучшего алгоритма обучения не имеет ценности из-за громадного числа случайных факторов, о которых по разным причинам отсутствует информация. В этой зоне может оказаться удобным второй алгоритм обучения, в соответствии с которым величина коррекции памяти БПП наиболее эффективно уменьшается с уменьшением рассогласования
на скорость вращения привода влияют многочисленные неучтенные воздействия. Поэтому детерминированный анализ процессов регулирования в некоторой микрозоне ошибок с точки зрения исследования передаточных свойств привода и формулировки наилучшего алгоритма обучения не имеет ценности из-за громадного числа случайных факторов, о которых по разным причинам отсутствует информация. В этой зоне может оказаться удобным второй алгоритм обучения, в соответствии с которым величина коррекции памяти БПП наиболее эффективно уменьшается с уменьшением рассогласования 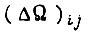 . В зоне же больших ошибок целесообразно применение третьего алгоритма обучения, тогда первый, алгоритм следует применить в промежуточной зоне между малыми и большими ошибками.
. В зоне же больших ошибок целесообразно применение третьего алгоритма обучения, тогда первый, алгоритм следует применить в промежуточной зоне между малыми и большими ошибками.
Рассмотрим процесс обучения путем перебора всех состояний памяти.
Для каждой совокупности 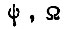 внутри такта обучения имеем общее число различных состояний сигнала
внутри такта обучения имеем общее число различных состояний сигнала 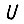 на выходе БПП, равное
на выходе БПП, равное 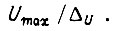 При переборе всех состояний элементов памяти вероятность нахождения правильного числа
При переборе всех состояний элементов памяти вероятность нахождения правильного числа 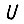 , при котором рассогласование
, при котором рассогласование 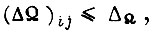 для БПП с двоичным выходом
для БПП с двоичным выходом
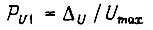
и для БПП о десятичным выходом
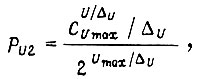
где 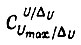 - число сочетаний из
- число сочетаний из 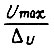 по
по 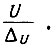
За 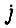 циклов обучения та же вероятность в
циклов обучения та же вероятность в 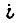 -м такте сигнала
-м такте сигнала 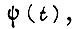
 после того как закончено обучение в
после того как закончено обучение в 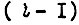 -м такте:
-м такте:
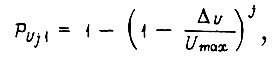
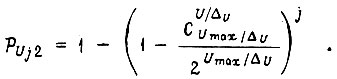
Эти выражения справедливы, если обучение системы начато от состояния полностью неорганизованной памяти.
Вероятность того, что система за 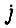 циклов полностью обучена одной функции
циклов полностью обучена одной функции 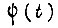 для БПП с двоичным выходом
для БПП с двоичным выходом
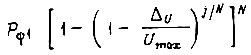
и для БПП с десятичным выходом
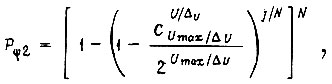
где 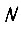 - число различных сочетаний амплитуд
- число различных сочетаний амплитуд 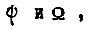 встречающихся в пределах цикла функции
встречающихся в пределах цикла функции 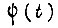 . Отсюда время обучения сигналу,
. Отсюда время обучения сигналу, 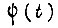
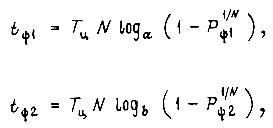
где

В процессе обучения одной совокупности значений 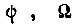 в пределах такта для одной заданной функции
в пределах такта для одной заданной функции 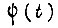 пока не найдена требуемая скорость
пока не найдена требуемая скорость 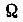 в предыдущем такте, происходит обучение различным совокупностям значений
в предыдущем такте, происходит обучение различным совокупностям значений 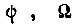 . Это обучение является дополнительным, но не необходимым для выработки правильной реакции привода на заданный сигнал
. Это обучение является дополнительным, но не необходимым для выработки правильной реакции привода на заданный сигнал 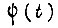 . Результаты такой организации памяти БПП имеют практическое значение в случае, когда для одной
. Результаты такой организации памяти БПП имеют практическое значение в случае, когда для одной 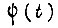 непредусмотренные по величине задающие воздействия будут выводить систему привода после обучения из желаемого диапазона ошибок движения и в отдельные такты появится рассогласование, большее
непредусмотренные по величине задающие воздействия будут выводить систему привода после обучения из желаемого диапазона ошибок движения и в отдельные такты появится рассогласование, большее 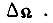
Обучение путем перебора всех состояний может быть применено во всей зоне ошибок 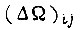 или только в микрозоне, где целесообразно также применение второго алгоритма обучения. При переборе всех состояний необходимо предусмотреть положительную обратную связь обучения, которая после того, как организация памяти закончилась, отключает выход устройства коррекции памяти от входа БПП.
или только в микрозоне, где целесообразно также применение второго алгоритма обучения. При переборе всех состояний необходимо предусмотреть положительную обратную связь обучения, которая после того, как организация памяти закончилась, отключает выход устройства коррекции памяти от входа БПП.
Состояние элементов памяти логической схемы в каждый момент времени есть результат двух противоположно направленных процессов. Первый представляет собой обучение системы привода, второй - воздействие среды в виде помех, переключающих элементы памяти, случайных возмущений, неконтролируемых датчиками и приложенных к силовой части, и изменений ее параметров. Суммарный процесс в динамической системе, оператор которой задан в виде обобщенной булевой функции, можно описать системой дифференциальных уравнений А. Н. Колмогорова
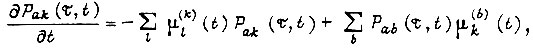
где 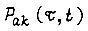 - условная вероятность пребывания системы в момент
- условная вероятность пребывания системы в момент 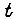 в состоянии
в состоянии 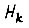 при условии, что в предшествующий момент
при условии, что в предшествующий момент 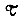 она находилась в состоянии
она находилась в состоянии 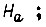
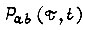 - условная вероятность пребывания системы в момент
- условная вероятность пребывания системы в момент 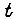 в состоянии
в состоянии 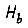 при условии, что в предшествующий момент
при условии, что в предшествующий момент 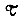 она находилась в состоянии
она находилась в состоянии 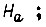
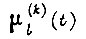 - интенсивность перехода системы из состояния
- интенсивность перехода системы из состояния 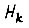 в состояние
в состояние 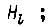
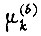 - интенсивность перехода системы из состояния
- интенсивность перехода системы из состояния 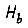 в состояние
в состояние 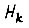 .
.
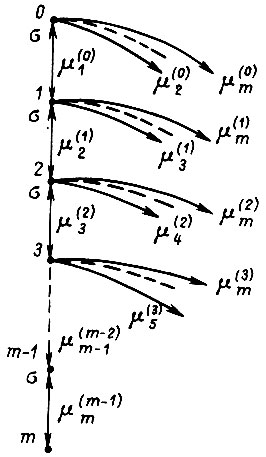
Рис. 62
На рис. 62 показана ветвь графа динамической системы. Здесь 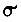 - интенсивность регенерации, возвращающей систему из каждого последующего состояния в ближайшее предыдущее в процессе обучения. Система дифференциальных уравнений имеет вид
- интенсивность регенерации, возвращающей систему из каждого последующего состояния в ближайшее предыдущее в процессе обучения. Система дифференциальных уравнений имеет вид
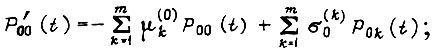
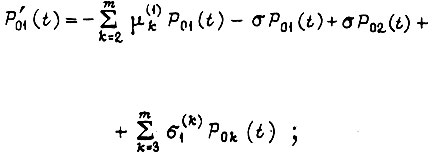
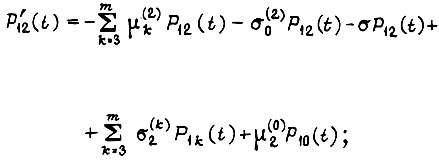
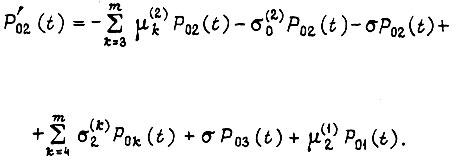
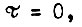
Рассматриваем однородный процесс во времени, поэтому допустим перенос начала отсчета 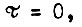 например, из состояния
например, из состояния 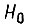 в состояние
в состояние 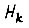 . Здесь
. Здесь 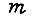 равно числу конъюнкций состояний двоичных разрядов
равно числу конъюнкций состояний двоичных разрядов 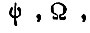 связанных с одной УС, для которых воздействием среды нарушено организованное состояние элементов памяти или состояние силовой части в сигналах или параметрах;
связанных с одной УС, для которых воздействием среды нарушено организованное состояние элементов памяти или состояние силовой части в сигналах или параметрах; 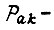 - условная вероятность нарушенного состояния для
- условная вероятность нарушенного состояния для 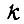 конъюнкций в момент времени
конъюнкций в момент времени 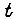 , если в момент
, если в момент 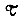 состояние было нарушено для
состояние было нарушено для 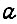 конъюнкций;
конъюнкций; 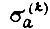 - интенсивность регенерации, т. е. перехода путем обучения из нарушенного состояния БПП для к конъюнкций в такое же состояние для
- интенсивность регенерации, т. е. перехода путем обучения из нарушенного состояния БПП для к конъюнкций в такое же состояние для 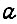 конъюнкций.
конъюнкций.
Осуществив преобразование Лапласа над левыми и правыми частями уравнений, вычисляем затем вероятность 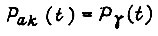 с помощью обратного преобразования
с помощью обратного преобразования
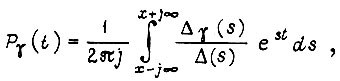
где 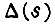 - главный определитель алгебраических уравнений;
- главный определитель алгебраических уравнений; 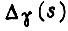 - определитель, получаемый из главного заменой элементов
- определитель, получаемый из главного заменой элементов 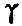 -го столбца соответствующими свободными членами.
-го столбца соответствующими свободными членами.
Для получения практически приемлемого вывода предположим, что обучение имеет место только между состояниями 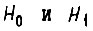 т. е. когда нарушены результаты организации элементов памяти для одной конъюнкции
т. е. когда нарушены результаты организации элементов памяти для одной конъюнкции 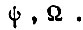 Реальная же система привода будет обладать лучшими свойствами, т. е. уменьшать средневероятностное рассогласование
Реальная же система привода будет обладать лучшими свойствами, т. е. уменьшать средневероятностное рассогласование 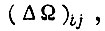 если учитывать вероятность истинности булевой функции, реализуемой узловой схемой, и наличие обучения между всеми состояниями
если учитывать вероятность истинности булевой функции, реализуемой узловой схемой, и наличие обучения между всеми состояниями 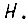 Система дифференциальных уравнений сводится к двум уравнениям:
Система дифференциальных уравнений сводится к двум уравнениям:
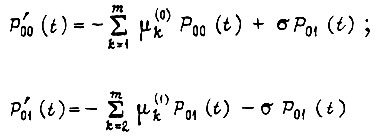
или с использованием оператора 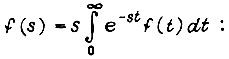
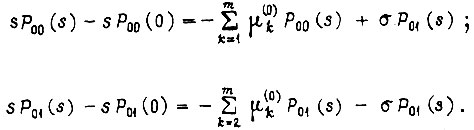
Решение системы двух уравнений:
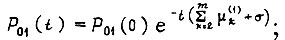
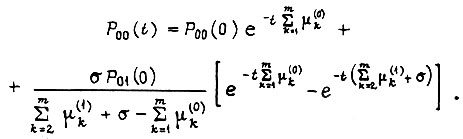
Устремим интенсивность обучения 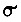 к бесконечности. Тогда
к бесконечности. Тогда
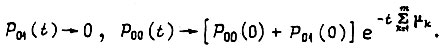
Итак, при 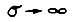 система никогда не находится в состоянии, нарушенном для одной конъюнкции
система никогда не находится в состоянии, нарушенном для одной конъюнкции 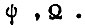 Для конечного значения
Для конечного значения 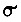 и заданного времени
и заданного времени 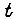 имеются два способа повысить работоспособность системы привода в условиях изменяющейся среды, т. е. эффективность адаптации. Первый способ заключается в увеличении
имеются два способа повысить работоспособность системы привода в условиях изменяющейся среды, т. е. эффективность адаптации. Первый способ заключается в увеличении 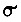 . Практически величина
. Практически величина 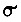 ограничена сверху техническим решением логической схемы и силовой части, а также частостью прихода конъюнкций
ограничена сверху техническим решением логической схемы и силовой части, а также частостью прихода конъюнкций 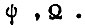 Поэтому, когда возможности первого способа исчерпаны, остается второй путь, который заключается в принятии мер по защите логической схемы, цепей согласования, преобразователей силовой части и каналов измерения
Поэтому, когда возможности первого способа исчерпаны, остается второй путь, который заключается в принятии мер по защите логической схемы, цепей согласования, преобразователей силовой части и каналов измерения 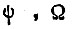 от воздействия помех и мер по снижению эффекта ухудшения характеристик привода из-за постепенных изменений его параметров. Вторым способом уменьшают суммы
от воздействия помех и мер по снижению эффекта ухудшения характеристик привода из-за постепенных изменений его параметров. Вторым способом уменьшают суммы 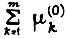 и
и 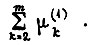
Формулой для 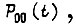 приведенной выше, можно воспользоваться, если известны
приведенной выше, можно воспользоваться, если известны 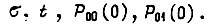 Приняв практически удовлетворительное значение
Приняв практически удовлетворительное значение 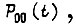 у а также значение
у а также значение 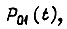 получаем величины
получаем величины 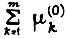 и
и 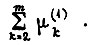 Сравнение этих сумм с суммами, известными из статистических сведений или же предположенными, количественно указывает на меры по дополнительному конструированию системы привода.
Сравнение этих сумм с суммами, известными из статистических сведений или же предположенными, количественно указывает на меры по дополнительному конструированию системы привода.
Определим величину интенсивности обучения 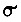 . Пусть функция
. Пусть функция 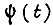 постоянно поступает на вход БПП. После того как закончилось обучение для
постоянно поступает на вход БПП. После того как закончилось обучение для 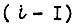 -го такта, все состояния элементов памяти БПП для
-го такта, все состояния элементов памяти БПП для 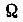 -го такте в первом цикле равновероятны. Тогда вероятность сведения ошибки
-го такте в первом цикле равновероятны. Тогда вероятность сведения ошибки 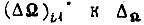 равна
равна
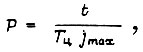
что справедливо в промежутке 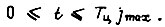 Число циклов
Число циклов 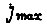 зависит от принятого алгоритма обучения. Если обучение идет по трем рассмотренным алгоритмам, то
зависит от принятого алгоритма обучения. Если обучение идет по трем рассмотренным алгоритмам, то
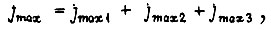
где 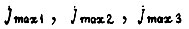 определяются из величин рассогласований, расположенных на границах каждой зоны. Вероятность
определяются из величин рассогласований, расположенных на границах каждой зоны. Вероятность 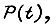 если
если 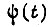 поступает непостоянно, есть
поступает непостоянно, есть
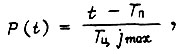
где 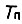 - суммарное время пауз между появлениями функции
- суммарное время пауз между появлениями функции 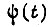 к моменту времени
к моменту времени 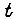 .
.
В дифференциальные уравнения А. Н. Колмогорова интенсивность 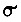 введена как параметр экспоненциального закона
введена как параметр экспоненциального закона 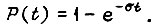 Разложив функцию
Разложив функцию 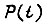 в ряд, воспользуемся первым членом разложения
в ряд, воспользуемся первым членом разложения
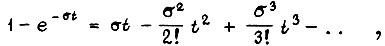
т. е.
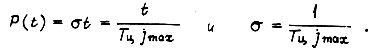
Другая формула 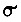
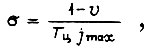
где 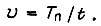
При обучении системы путем перебора всех состояний вероятность нахождения правильного числа U в 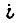 -м такте
-м такте 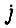 -го цикла для БПП с двоичным выходом
-го цикла для БПП с двоичным выходом
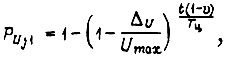
для БПП с десятичным выходом
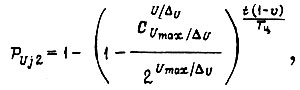
Отсюда интенсивность обучения 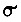 в первом случае
в первом случае
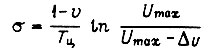
и во втором -
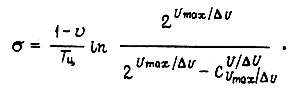
Определим интенсивность переходов 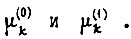 Вероятность перехода обученной системы из-за воздействия среды из состояния
Вероятность перехода обученной системы из-за воздействия среды из состояния 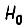 в состояние
в состояние 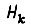
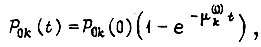
из состояния 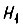 в состояние
в состояние 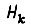 -
-
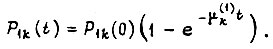
Величины 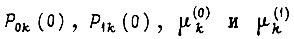 известны, если задана двумерная плотность распределения вероятностей величины мощности, трансформируемой средой в систему, и времени появления этой мощности. Интенсивность перехода
известны, если задана двумерная плотность распределения вероятностей величины мощности, трансформируемой средой в систему, и времени появления этой мощности. Интенсивность перехода 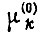 - параметр экспоненциального закона, описывающего нарушение состояния к элементов памяти, связанных с различными конъюнкциями
- параметр экспоненциального закона, описывающего нарушение состояния к элементов памяти, связанных с различными конъюнкциями 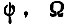 в момент времени
в момент времени 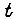 . Интенсивность
. Интенсивность 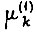 параметр, характеризующий нарушение
параметр, характеризующий нарушение 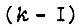 элементов памяти.
элементов памяти.
Эффект адаптации тем выше, чем меньше время цикла входного сигнала 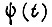 и промежутки времени между циклами, а также чем выше заданная предельная ошибка обучения. Этот вывод следует из вышеприведенных формул для
и промежутки времени между циклами, а также чем выше заданная предельная ошибка обучения. Этот вывод следует из вышеприведенных формул для 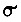 . При обучении же по алгоритму превалирующую роль играет величина коэффициентов γ , однако их выбор ограничен пределами, которые могут быть установлены из соображений сходимости процесса обучения нелинейной системы. Величина γ определяет число циклов обучения
. При обучении же по алгоритму превалирующую роль играет величина коэффициентов γ , однако их выбор ограничен пределами, которые могут быть установлены из соображений сходимости процесса обучения нелинейной системы. Величина γ определяет число циклов обучения 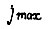 , вычисление которого можно произвести, предполагая систему линейной, если влияние нелинейности на
, вычисление которого можно произвести, предполагая систему линейной, если влияние нелинейности на 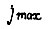 свести к равновероятности появления всех ситуаций, образующих состояние необученной системы, т. е. появления отдельных значений U внутри такта.
свести к равновероятности появления всех ситуаций, образующих состояние необученной системы, т. е. появления отдельных значений U внутри такта.
Из рассмотрения трех алгоритмов обучения следует, что процесс обучения является расходящимся, если:

Передаточная функция силовой части, не замкнутой обратными связями, со скоростью 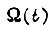 на выходе
на выходе
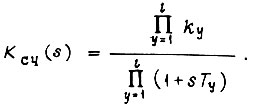
Предполагая, что длительность такта обучения 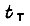 - практически малая величина, такая, что
- практически малая величина, такая, что  получаем
получаем
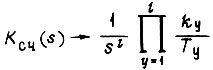
для ступенчатого приращения выходного сигнала логической схемы в пределах такта. Оригинал изображения 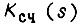
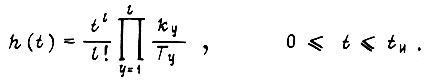
Тогда в соответствии с тремя алгоритмами обучения справедливо одно из выражений:
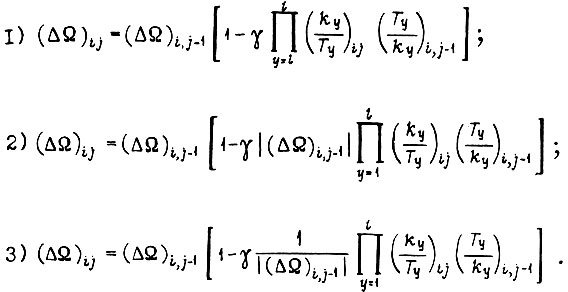
Процесс обучения является сходящимся, если 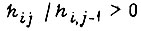 и, кроме того, выполняются неравенства:
и, кроме того, выполняются неравенства:
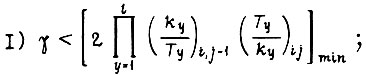
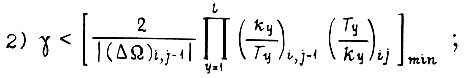
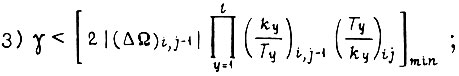
Соблюдение этих неравенств приводит к тому, что рассогласование 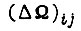 в процессе обучения монотонно убывает по абсолютной величине от цикла к циклу сигнала
в процессе обучения монотонно убывает по абсолютной величине от цикла к циклу сигнала 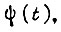 стремясь к
стремясь к 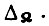 Однако время обучения может оказаться недопустимо большим. Увеличение же коэффициентов γ приводит к уменьшению длительности обучения, но возникает опасность установления незатухающих колебаний скорости Ω внутри такта при обучении.
Однако время обучения может оказаться недопустимо большим. Увеличение же коэффициентов γ приводит к уменьшению длительности обучения, но возникает опасность установления незатухающих колебаний скорости Ω внутри такта при обучении.
Рассмотрим сходимость процесса обучения системы привода более подробно. Если обучение происходит на практически горизонтальном участке функции 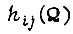 или в линейной системе, то условия сходимости имеют вид:
или в линейной системе, то условия сходимости имеют вид:
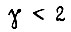 - для первого,
- для первого,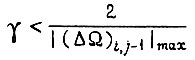 - для второго,
- для второго,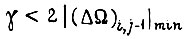 - для третьего алгоритма.
- для третьего алгоритма.
Если коррекция состояния элементов памяти ЛС производится при движении вдоль циклов по монотонно убывающему участку функции 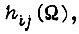 то при выполнении условий сходимости для горизонтального участка получаем каждый раз
то при выполнении условий сходимости для горизонтального участка получаем каждый раз 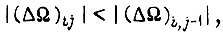 так как
так как 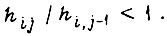
При перемещении вверх по этому же участку функции 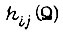 не исключено равенство
не исключено равенство 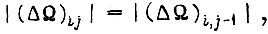 а также неравенство
а также неравенство 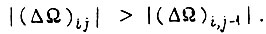 Однако после того, как требуемая скорость вращения
Однако после того, как требуемая скорость вращения 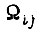 пройдена, происходит реверс изменения величины U и начинается движение по участку функции
пройдена, происходит реверс изменения величины U и начинается движение по участку функции 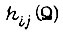 до тех пор, пока рассогласование не станет равным
до тех пор, пока рассогласование не станет равным 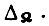 Время, затрачиваемое на перемещение вниз, всегда больше при заданном γ, чем длительность перемещения вверх.
Время, затрачиваемое на перемещение вниз, всегда больше при заданном γ, чем длительность перемещения вверх.
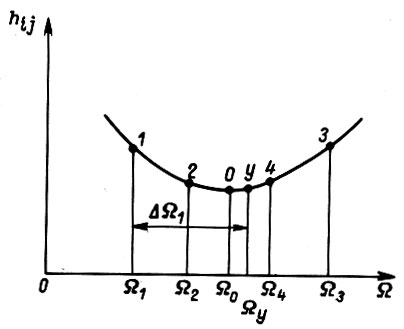
Рис. 63
На рис. 63 изображена функция 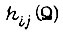 параболического вида, имеющая точку экстремума 0. Представим, что после некоторого числа циклов обучения состояние системы в
параболического вида, имеющая точку экстремума 0. Представим, что после некоторого числа циклов обучения состояние системы в 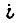 -м такте характеризуется скоростью
-м такте характеризуется скоростью 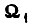 внутри импульса U;
внутри импульса U; 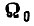 - скорость внутри паузы. Требуемое состояние определяется скоростью
- скорость внутри паузы. Требуемое состояние определяется скоростью 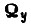 внутри импульса U. Физически реализуемым является вариант колебательного движения при обучении вдоль точек 1, 2, 3, 4 по траектории 1-2-3-4-1-2-... .Устойчивые колебания около точки, расположенной слева или справа от точки экстремума y, имеют неодинаковые амплитуды, что объясняется неодинаковостью нелинейности
внутри импульса U. Физически реализуемым является вариант колебательного движения при обучении вдоль точек 1, 2, 3, 4 по траектории 1-2-3-4-1-2-... .Устойчивые колебания около точки, расположенной слева или справа от точки экстремума y, имеют неодинаковые амплитуды, что объясняется неодинаковостью нелинейности 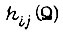 слева и справа от такой точки. Любое такое колебание может быть представлено как сумма гармонических функций и постоянной составляющей. Следовательно, устранение устойчивых колебаний
слева и справа от такой точки. Любое такое колебание может быть представлено как сумма гармонических функций и постоянной составляющей. Следовательно, устранение устойчивых колебаний 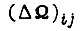 сводится к устранению симметричных колебаний, которые могут существовать только около точки 0. Точка y расположена рядом с
сводится к устранению симметричных колебаний, которые могут существовать только около точки 0. Точка y расположена рядом с 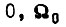 отличается от
отличается от 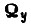 не более чем на
не более чем на 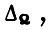 если обучение в предыдущем такте закончено. Скорости
если обучение в предыдущем такте закончено. Скорости 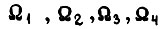 - скорости внутри импульса U в рассматриваемом такте. При обучении по первому алгоритму колебания описываются уравнениями
- скорости внутри импульса U в рассматриваемом такте. При обучении по первому алгоритму колебания описываются уравнениями
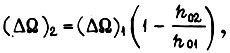
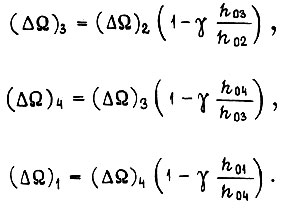
Здесь 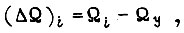 индексы при h указывают порядок перемещения вдоль траектории внутри импульса U. Общее уравнение
индексы при h указывают порядок перемещения вдоль траектории внутри импульса U. Общее уравнение
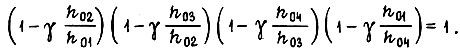
Сделаем допущение о том, что зону экстремума 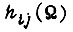 в которой происходят колебания, можно аппроксимировать зоной, в которой
в которой происходят колебания, можно аппроксимировать зоной, в которой 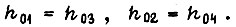
Тогда 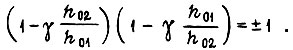 Обозначим
Обозначим 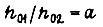 и рассмотрим уравнение
и рассмотрим уравнение 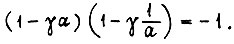
Решение уравнения 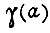 имеет вид
имеет вид
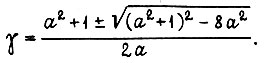
Коэффициент γ - вещественное число при условии 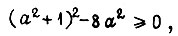 т. е.
т. е. 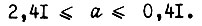 Функция
Функция 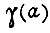 изображена на рис. 64. Из него следует, что при
изображена на рис. 64. Из него следует, что при 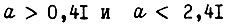 колебания рассмотренного типа при обучении не имеют места. Очевидно, условие возникновения колебаний
колебания рассмотренного типа при обучении не имеют места. Очевидно, условие возникновения колебаний 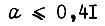 можно получить вместо
можно получить вместо 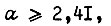 и наоборот, если через а обозначить отношение
и наоборот, если через а обозначить отношение 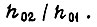
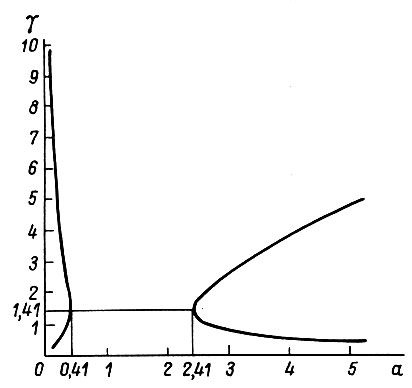
Рис. 64
Рассмотрим теперь уравнение
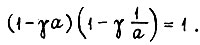
Решение 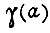
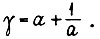
Минимальное значение γ равно 2 при 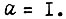 Учитывая, что при проектировании алгоритма всегда следует выбирать
Учитывая, что при проектировании алгоритма всегда следует выбирать 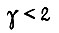 из условия сходимости обучения на горизонтальном участке функции
из условия сходимости обучения на горизонтальном участке функции 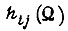 данное решение из дальнейшего рассмотрения исключением.
данное решение из дальнейшего рассмотрения исключением.
В общем случае колебательное движение, установившееся в зоне, ограниченной точками 1 и 3 (см. рис. 63) с амплитудой вплоть до границ, имеет период из числа циклов, большего четырех, и описывается уравнением
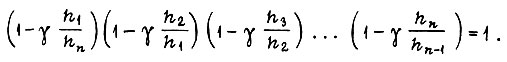
Исходя из возможности таких колебаний, получаем, что после точки 1 скорость достигает величины 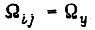 за число циклов, большее двух. Но такое обучение происходит, следовательно, при другом значении коэффициента
за число циклов, большее двух. Но такое обучение происходит, следовательно, при другом значении коэффициента 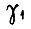 . Ему соответствует равенство
. Ему соответствует равенство
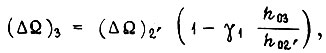
где точка 2' не совпадает с точкой 2 и получена переходом из некоторой точки 1'. Однако между точками 1 и 3 невозможны колебания с периодом, состоящим из числа циклов более четырех для 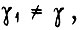 если с коэффициентом
если с коэффициентом 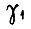 имеют место колебания в зоне
имеют место колебания в зоне 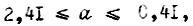 рассмотренные выше. Аппроксимируя участки I-0 и 0-3 функции
рассмотренные выше. Аппроксимируя участки I-0 и 0-3 функции 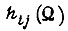 (см. рис. 63) прямыми линиями, получаем, что
(см. рис. 63) прямыми линиями, получаем, что
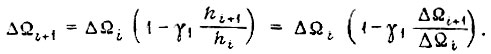
Тогда, если период колебаний состоит из n циклов, справедливо соотношение
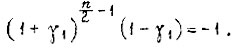
Если это условие выполняется при фиксированном 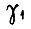 и
и 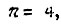 то, очевидно, оно не выполняется при том же
то, очевидно, оно не выполняется при том же 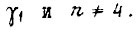
Итак, в области 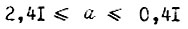 возможны для каждого у, выбираемого по графику рис. 64, установившиеся колебания скорости
возможны для каждого у, выбираемого по графику рис. 64, установившиеся колебания скорости 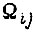 только с периодом, состоящим из четырех циклов. О наличии колебаний с периодом, состоящим из числа циклов, большего четырех, имеет смысл говорить для области
только с периодом, состоящим из четырех циклов. О наличии колебаний с периодом, состоящим из числа циклов, большего четырех, имеет смысл говорить для области 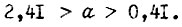
Установившиеся колебания скорости при обучении по второму алгоритму описываются аналогичным уравнением
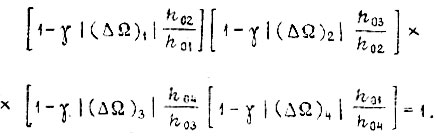
Допускаем, что 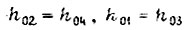 и
и 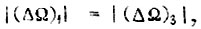
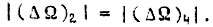 Тогда
Тогда 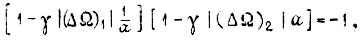 где
где 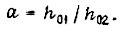 Случай, когда правая часть равна единице, неприемлем.
Случай, когда правая часть равна единице, неприемлем.
В результате
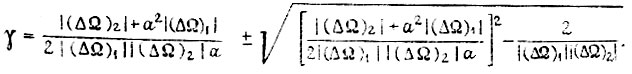
Если бы соблюдалось условие 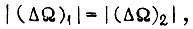 то справедливым оказалось бы равенство
то справедливым оказалось бы равенство
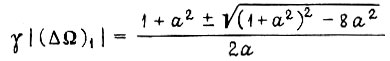
и функция 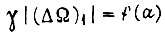 стала бы эквивалентной функции
стала бы эквивалентной функции 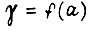 при обучении по первому алгоритму, изображенной на рис. 64. Однако в действительности
при обучении по первому алгоритму, изображенной на рис. 64. Однако в действительности 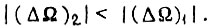 Учитывая это, перепишем полученный результат для γ иначе:
Учитывая это, перепишем полученный результат для γ иначе:
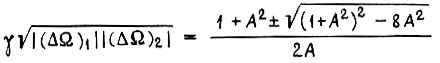
где 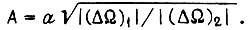
В соответствии с рис. 64 устойчивые колебания с периодом, равным, четырем циклам, при обучении по второму алгоритму имеют место в зоне 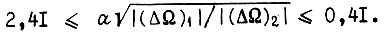 Каждому значению
Каждому значению 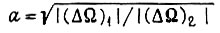 соответствует определенная величина
соответствует определенная величина 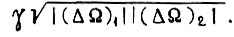 При проектировании второго алгоритма в рабочей зоне характеристики
При проектировании второго алгоритма в рабочей зоне характеристики 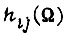 необходимо перебрать все комбинации
необходимо перебрать все комбинации 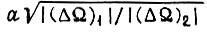 в области
в области 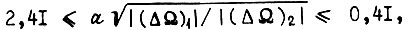 где
где 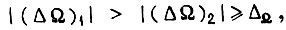 и определить для них
и определить для них 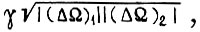 запретив затем все найденные значения γ.
запретив затем все найденные значения γ.
Установившиеся колебания с периодом из четырех циклов при обучении по третьему алгоритму описываются уравнением
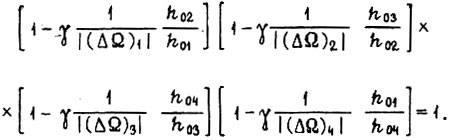
Сделаем допущение о том, что 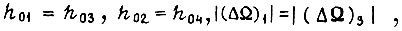
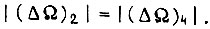 Тогда
Тогда 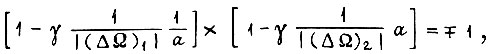 где
где 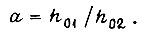 Отсюда
Отсюда
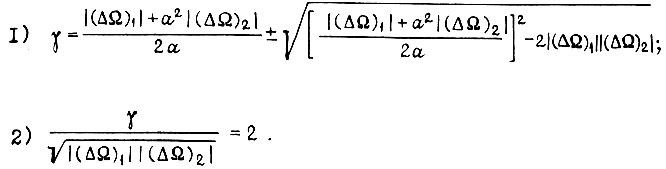
Так как 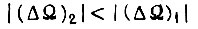 (см. рис. 63), то второе решение эквивалентно соблюдению неравенства
(см. рис. 63), то второе решение эквивалентно соблюдению неравенства 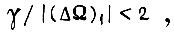 что подтверждает условие сходимости процесса обучения на горизонтальном участке функции
что подтверждает условие сходимости процесса обучения на горизонтальном участке функции 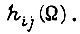 Первое решение перепишем в виде
Первое решение перепишем в виде
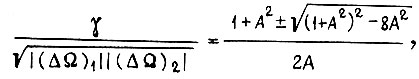
где 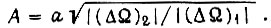
Устойчивые колебания скорости 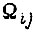 с периодом, равным четырем циклам, имеют место (в соответствии с рис. 64) при обучении по третьему алгоритму в зоне
с периодом, равным четырем циклам, имеют место (в соответствии с рис. 64) при обучении по третьему алгоритму в зоне 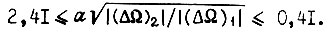 При проектировании третьего алгоритма необходимо в рабочей зоне характеристики
При проектировании третьего алгоритма необходимо в рабочей зоне характеристики 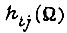 перебрать все комбинации
перебрать все комбинации 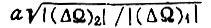 в области, где существуют колебания, причем
в области, где существуют колебания, причем 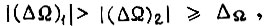 и определить для них
и определить для них 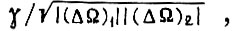 запретив затем все найденные значения γ.
запретив затем все найденные значения γ.
Обучение системы по первому алгоритму может свестись внутри такта к установлению колебаний 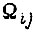 с периодом, равным четырем циклам, если
с периодом, равным четырем циклам, если 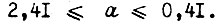 При проектировании первого алгоритма необходимо найти в рабочей области характеристики
При проектировании первого алгоритма необходимо найти в рабочей области характеристики 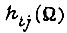 с минимумом
с минимумом 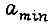 или
или 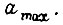 В общем виде при
В общем виде при
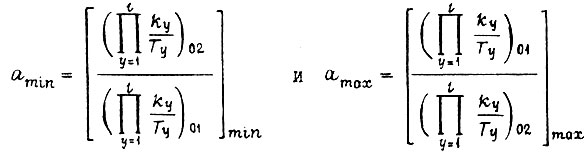
Таким образом, для нахождения 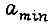 или
или 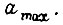 требуется построить характеристику силовой части
требуется построить характеристику силовой части 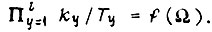 Если
Если 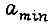 вычислить как отношение минимальной амплитуды
вычислить как отношение минимальной амплитуды 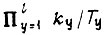 к максимальной в рабочей области характеристики
к максимальной в рабочей области характеристики 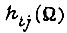 с минимумом, а
с минимумом, а 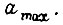 - как отношение максимальной амплитуды к минимальной, то это позволяет при выборе устранить устойчивые колебания в области
- как отношение максимальной амплитуды к минимальной, то это позволяет при выборе устранить устойчивые колебания в области 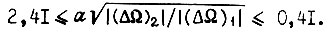 Коэффициент γ следует выбирать из графика функции
Коэффициент γ следует выбирать из графика функции 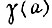 (рис. 64) так, чтобы ему соответствовала величина
(рис. 64) так, чтобы ему соответствовала величина 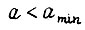 или
или 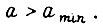 Величина γ должна также гарантировать отсутствие любых устойчивых колебаний
Величина γ должна также гарантировать отсутствие любых устойчивых колебаний 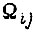 в области
в области 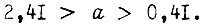 Выбор коэффициента γ для второго алгоритма обучения производят так, что в области, где возможны колебания с периодом из четырех циклов, ему соответствует выполнение неравенств
Выбор коэффициента γ для второго алгоритма обучения производят так, что в области, где возможны колебания с периодом из четырех циклов, ему соответствует выполнение неравенств
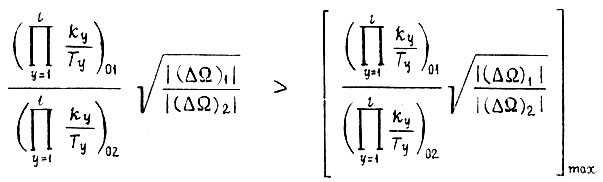
или
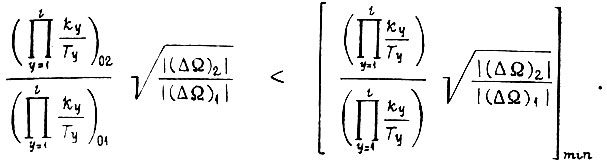
Аналогичный выбор коэффициента γ для третьего алгоритма производится так, чтобы соблюдались эти же неравенства, но 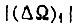 и
и 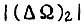 следует поменять местами.
следует поменять местами.
Для характеристики 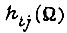 с максимумом устойчивые колебания около точки экстремума невозможны. Например, для периода, состоящего из четырех циклов, и первого алгоритма
с максимумом устойчивые колебания около точки экстремума невозможны. Например, для периода, состоящего из четырех циклов, и первого алгоритма
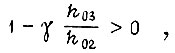
если 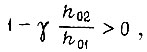
что соответствует сходящемуся процессу обучения при выполнении условия сходимости на горизонтальном участке функции 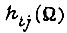 .
.
Длительность обучения определяется выбором коэффициентов γ. Этот выбор производится из условий сходимости процесса на горизонтальных, монотонно убывающих и возрастающих участках функции 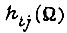 , а также на участках с точками минимумов. Отвлекаясь от соображений сходимости, определим коэффициенты, которым соответствует наименьшее время, затрачиваемое на обучение. Для этого представим функцию
, а также на участках с точками минимумов. Отвлекаясь от соображений сходимости, определим коэффициенты, которым соответствует наименьшее время, затрачиваемое на обучение. Для этого представим функцию 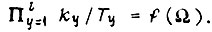 дискретными значениями, дискретизировав ось Ω отрезком, равным
дискретными значениями, дискретизировав ось Ω отрезком, равным 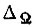 , и усреднив в пределах каждого отрезка ординаты. В данном случае будем исходить из того, что переходная функция СЧ известна. Наименьшему времени обучения системы привода в пределах такта соответствует число циклов, равное единице. Предполагая равновероятными все ситуации, когда за один цикл требуется перейти от некоторого произвольного значения Ω к другому, для которого ошибка
, и усреднив в пределах каждого отрезка ординаты. В данном случае будем исходить из того, что переходная функция СЧ известна. Наименьшему времени обучения системы привода в пределах такта соответствует число циклов, равное единице. Предполагая равновероятными все ситуации, когда за один цикл требуется перейти от некоторого произвольного значения Ω к другому, для которого ошибка 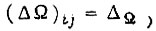 построим функцию распределения вероятностей случайной величины
построим функцию распределения вероятностей случайной величины
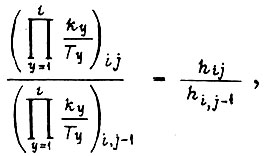
исследовав функцию 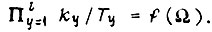 Математическое ожидание
Математическое ожидание 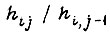 равно
равно
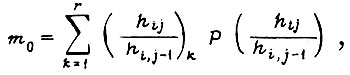
где 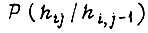 - функция распределения; r - общее число дискретных значений
- функция распределения; r - общее число дискретных значений 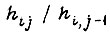 . Величину
. Величину 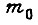 свяжем с коэффициентом γ с помощью формул:
свяжем с коэффициентом γ с помощью формул:
для первого алгоритма обучения
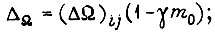
для второго
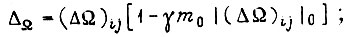
для третьего
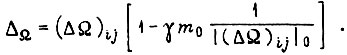
Устремив 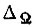 к нулю, получим: в первом случае
к нулю, получим: в первом случае 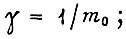 во втором
во втором 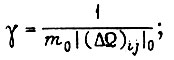 в третьем
в третьем 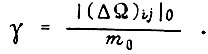 Здесь
Здесь 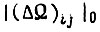 - средневероятностная величина
- средневероятностная величина 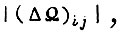 т. е.
т. е.
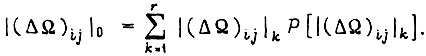
Если длительность обучения является удовлетворительной для коэффициентов γ, получаемых только из соображений сходимости, а основным процессом необходимо считать постоянное переобучение в условиях изменяющейся среды и износа элементов, то величины 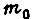 и
и 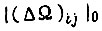 определяют, исследуя характеристику
определяют, исследуя характеристику 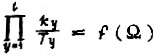 и располагая при этом статистическими сведениями о появлении отдельных ситуаций перехода от одних значений Ω к другим.
и располагая при этом статистическими сведениями о появлении отдельных ситуаций перехода от одних значений Ω к другим.
Коэффициенты γ, как функции 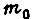
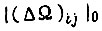 , соответствуют наиболее быстрому обучению в статистическом смысле. Однако величина γ ограничивается условиями сходимости процесса обучения. Если γ определены из этих условий, длительность обучения в одном такте для нелинейной силовой части может быть подсчитана по формулам:
, соответствуют наиболее быстрому обучению в статистическом смысле. Однако величина γ ограничивается условиями сходимости процесса обучения. Если γ определены из этих условий, длительность обучения в одном такте для нелинейной силовой части может быть подсчитана по формулам:
для первого алгоритма
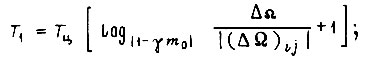
для третьего
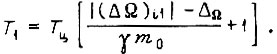
Используя величину математического ожидания 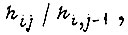 можно вычислить также время
можно вычислить также время 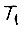 и при обучении по второму алгоритму .
и при обучении по второму алгоритму .
Имея в виду целесообразность применения в микрозоне рассогласований 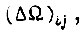 где детерминированный анализ характеристик СЧ не имеет смысла, второго алгоритма обучения, в большой зоне ошибок - третьего и в промежуточной зоне - первого алгоритма, следует определять собственные значения
где детерминированный анализ характеристик СЧ не имеет смысла, второго алгоритма обучения, в большой зоне ошибок - третьего и в промежуточной зоне - первого алгоритма, следует определять собственные значения 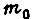 и
и 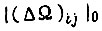 в каждой области Ω, соответствующей своей зоне
в каждой области Ω, соответствующей своей зоне 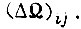 Тогда коэффициенты γ для системы, обучающейся наиболее быстро в статистическом смысле:
Тогда коэффициенты γ для системы, обучающейся наиболее быстро в статистическом смысле:
по второму алгоритму
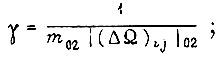
по первому
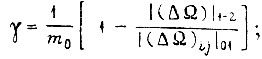
по третьему
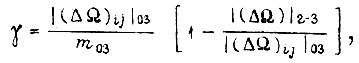
где 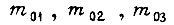 и
и 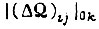 - математические ожидания
- математические ожидания 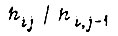 и
и 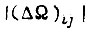 в соответствующей зоне рассогласований;
в соответствующей зоне рассогласований; 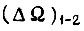 - граничное рассогласование между первой и второй зонами;
- граничное рассогласование между первой и второй зонами; 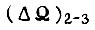 - граничное рассогласование между второй и третьей зонами, причем в первой зоне действует второй алгоритм, во второй - первый, в третьей - третий.
- граничное рассогласование между второй и третьей зонами, причем в первой зоне действует второй алгоритм, во второй - первый, в третьей - третий.
Длительность обучения внутри такта, если коэффициенты γ выбраны из условия сходимости процесса, определяются:
для первого алгоритма
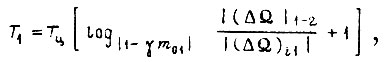
для третьего
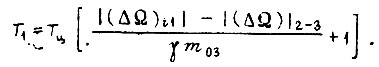
Выбор величины 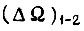 производится из физических соображений, выбор
производится из физических соображений, выбор 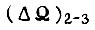 - путем вычислений с уточнением величины γ из условий сходимости и окончательно - из минимальной длительности обучения в области, состоящей из второй и третьей зон.
- путем вычислений с уточнением величины γ из условий сходимости и окончательно - из минимальной длительности обучения в области, состоящей из второй и третьей зон.
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'