
4. Проектирование алгоритма обучения
Зная рассогласование по скорости 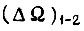 и выбрав ряд значений
и выбрав ряд значений 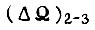 , которые расположены на границах зон с разными алгоритмами обучения, определяем коэффициенты γ из условия отсутствия устойчивых колебаний
, которые расположены на границах зон с разными алгоритмами обучения, определяем коэффициенты γ из условия отсутствия устойчивых колебаний 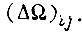 Для функции
Для функции 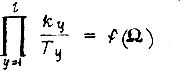 , имеющей точку минимума, коэффициенты у определяем:
, имеющей точку минимума, коэффициенты у определяем:
1) из условия сходимости обучения на горизонтальном участке функции 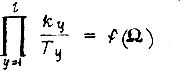 :
:
для первого алгоритма 
для второго 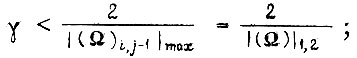
для третьего 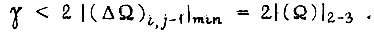
2) из условия отсутствия симметричных колебаний с периодом из четырех циклов обучения:
для первого алгоритма величину γ выбираем такой, что по формуле
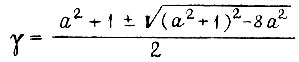
она соответствует
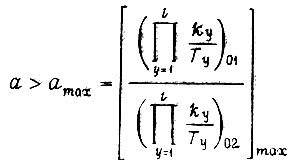
или
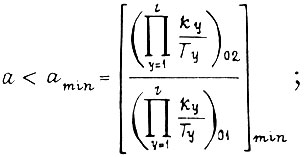
для второго алгоритма пользуемся той же формулой 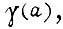 что и для первого алгоритма, поступая аналогично, однако полагают вместо a величину
что и для первого алгоритма, поступая аналогично, однако полагают вместо a величину 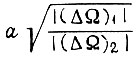 и вместо γ произведение
и вместо γ произведение
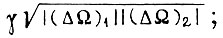
для третьего алгоритма поступаем аналогично, полагая в формуле 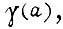 для первого алгоритма вместо γ величину
для первого алгоритма вместо γ величину 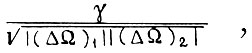 а вместо a произведение
а вместо a произведение 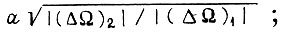
3) из условия отсутствия других устойчивых колебаний, пользуясь общим условием сходимости обучения:
для первого алгоритма
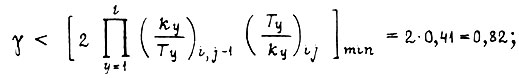
для второго
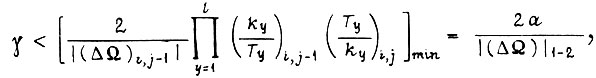
где a берут из условия 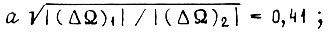
для третьего
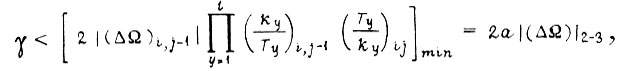
где 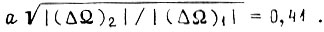
Если зона, где возможны колебания с периодом из четырех циклов, отсутствует, то для третьего условия вместо значения 0,41 берут то значение, которое реально существует при каждом алгоритме. Везде полагаем, что 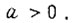 В данном случае условия сходимости процесса обучения применяются для устранения всех устойчивых колебаний, кроме колебаний с периодом из четырех циклов. После тройного выбора коэффициентов γ получаем их окончательные значения, которые соответствуют сходящемуся процессу обучения. Если функция
В данном случае условия сходимости процесса обучения применяются для устранения всех устойчивых колебаний, кроме колебаний с периодом из четырех циклов. После тройного выбора коэффициентов γ получаем их окончательные значения, которые соответствуют сходящемуся процессу обучения. Если функция 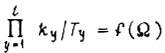 имеет только горизонтальные и монотонно изменяющиеся участки, то коэффициенты γ определяют из условия сходимости обучения на горизонтальном участке.
имеет только горизонтальные и монотонно изменяющиеся участки, то коэффициенты γ определяют из условия сходимости обучения на горизонтальном участке.
Выбранные коэффициенты γ не гарантируют, однако, что устойчивые колебания не возникнут в процессе переобучения с течением времени из-за постепенных изменений параметров привода. Допуская нормальный закон распределения вероятностей отдельных значений 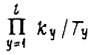 для заданных Ω и момента времени t, имеем формулу плотности распределения
для заданных Ω и момента времени t, имеем формулу плотности распределения
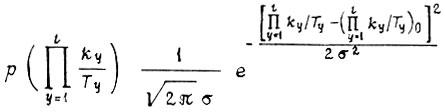
Зная среднеквадратичное отклонение σ, по правилу трех сигм >> находим максимальное практически возможное приращение 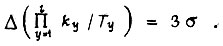 Приращения, найденные для каждого t и Ω, позволяют уточнить величины коэффициентов γ для новых значений a.
Приращения, найденные для каждого t и Ω, позволяют уточнить величины коэффициентов γ для новых значений a.
Если при проектировании обучаемой системы имеется возможность путем эксперимента получить функцию 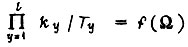 и, следовательно, коэффициенты γ для системы привода, наиболее быстродействующей в статистическом смысле, то эти коэффициенты следует учесть, приближая к ним по возможности выбираемые значения γ из условий сходимости процесса обучения. Аналогично следует поступить, если проектировщик располагает статистическими сведениями о рассогласованиях
и, следовательно, коэффициенты γ для системы привода, наиболее быстродействующей в статистическом смысле, то эти коэффициенты следует учесть, приближая к ним по возможности выбираемые значения γ из условий сходимости процесса обучения. Аналогично следует поступить, если проектировщик располагает статистическими сведениями о рассогласованиях 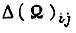 при переобучении.
при переобучении.
Скорость 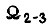 окончательно выбирается так, что она соответствует коэффициентам γ, для которых суммарная длительность обучения по первому и третьему алгоритмам минимальна.
окончательно выбирается так, что она соответствует коэффициентам γ, для которых суммарная длительность обучения по первому и третьему алгоритмам минимальна.
При работе двигателя на низких скоростях порядка I об/мин приходится учитывать вместо характеристики 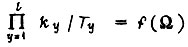 функцию
функцию 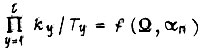 где
где 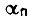 - путь, проходимый приводом. В этом случае успешное обучение возможно, если в логическую схему в каждом такте поступает информация об
- путь, проходимый приводом. В этом случае успешное обучение возможно, если в логическую схему в каждом такте поступает информация об 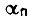 . При выборе коэффициентов γ величина
. При выборе коэффициентов γ величина 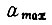 берется наибольшей, а
берется наибольшей, а 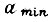 - наименьшей из всей области изменения
- наименьшей из всей области изменения 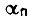 .
.
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'